ECOL 8000 Ecological Modelingfor the terrified Quick anonymous

ECOL 8000 Ecological Modeling(for the terrified? )

Quick (anonymous) quiz Please rank the following statements on a 1 -5 scale: 1 strongly agree, 2 agree, 3 neutral, 4 disagree, 5 strongly disagree A. I understand how and why mathematical models are used in Ecology B. I feel comfortable critically reading or reviewing ecology papers featuring mathematical models C. I know how to build models to answer ecological questions D. I can perform some simple analysis of math models (e. g. curve sketching or ”back of the envelope” calculations E. I plan to incorporate some mathematical modeling in my research

Some goals of this module • Demystifying modeling. Why it’s done & how it’s done • Using models as tools to sharpen research questions • Increase fluency in reading/translating equations, the assumptions underlying them • How to build a model • Simple tricks for gaining intuition before running to a computer

Module structure • Weeks 1 -2: we’ll work through some simple mathematical models, from the ground up, gradually building in complexity • Case studies of model building and simplification to gain insight into ecological questions • Weeks 2 -3: build your own model to address your chosen question

The why and how of math models Kokko’s “Modelling for Field Biologists” • how are models used in basic and applied science? • How complex should a model be? • Are wrong models useful? • Can a model ever be ‘too right? ’

The taxonomy of models • Modeling taxonomy – conceptual vs mathematical vs statistical • Model building: what do boxes and arrows represent? How do they relate to equations? Model terminology: • Discrete vs continuous? • Deterministic versus stochastic? Individual-based? When should these different model types be used?

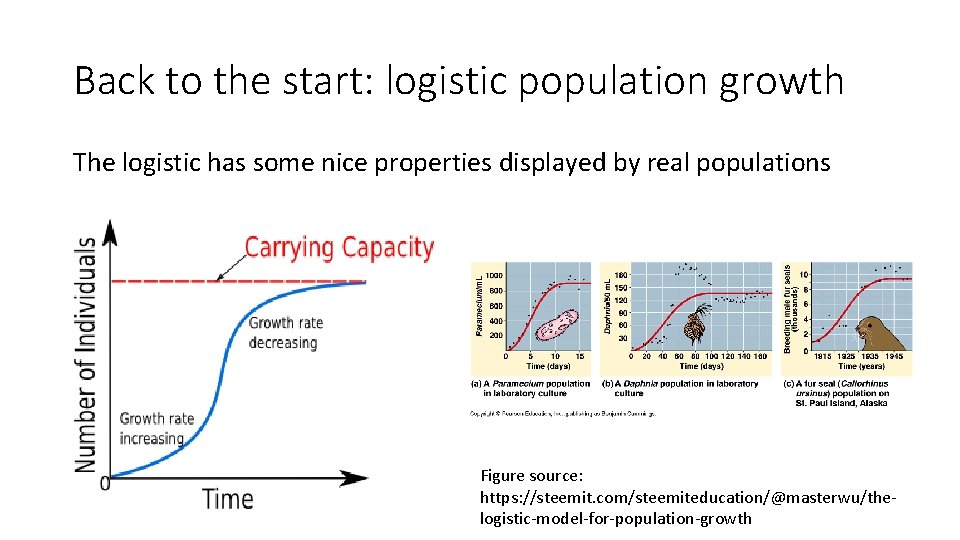
Back to the start: logistic population growth •

Back to the start: logistic population growth The logistic has some nice properties displayed by real populations Figure source: https: //steemit. com/steemiteducation/@masterwu/thelogistic-model-for-population-growth

Over to you – model building But is this just coincidence? What mechanisms underlie logistic growth? • In groups, draw a conceptual model (boxes and arrows) to represent processes by which a population changes over time • Turn your arrows into hypotheses: how do inputs and outputs into the boxes depend on your state variables? , and how do you write these mathematically? • Put these together into an equation: how do the parameters in your proposed functions relate to r and K?

Is your simple model reasonable? The logistic equation assumes per capita birth and death rates are linear functions of population size, but doesn’t include the dynamics of resources explicitly. What if we include resources as a state variable?

For next time • The following model describes constant effort harvesting: effort =E • What is “effort”? What is “q”? what units are they measured in? • Plot the rate of change of population size (d. N/dt) versus N and interpret these graphs. • Solve at equilibrium to express population size as a function of effort (set d. N/dt=0 and write N as a function of E) • What does catch (q. EN) look like as a function of effort at equilibrium?

Parting thoughts • Models are useful as thinking aids, not just for quantitative prediction • Forces us to crystallize our questions and simplify conceptually (analogy to microcosm experiments) • complex models aren’t necessarily useful or accurate! • Flowchart approach to building models – boxes are state variables, arrows indicate processes that increase or decrease state variables, equations represent the net effect of these arrows on the rate of change of variables