ECMWF INTEGRATED FORECASTING SYSTEM IFS WENJUN CUI ATMO

ECMWF INTEGRATED FORECASTING SYSTEM (IFS) WENJUN CUI ATMO 588

BACKGROUND The comprehensive Earth-system model developed at ECMWF in co-operation with Météo- France forms the basis for all data assimilation and forecasting activities. Initially the IFS was developed only for weather forecasting, but it evolved into a generic global model and now includes the modeling of the atmospheric composition. A free software called Open. IFS can be downloaded online but requires a ECMWF license. The dynamical core of the IFS is hydrostatic, two-time-level, semi-implicit, semi-Lagrangian and applies spectral transforms between grid-point space and spectral space. 1

DEVELOPING A SEMI-LAGRANGIAN MODEL Starting with Eulerian model Discretisation with semi-implicit corrections Vertical discretisation Time discretisation Applied the fast spectral transform method Paring an horizontal grid with a spectral truncation Time-stepping Time filtering Numerical filters Semi-Lagrangian formulation Finding departure point Semi-Lagrangian discretisation Time-stepping Modified semi-Lagrangian equations Two-time-level semi-Lagrangian scheme

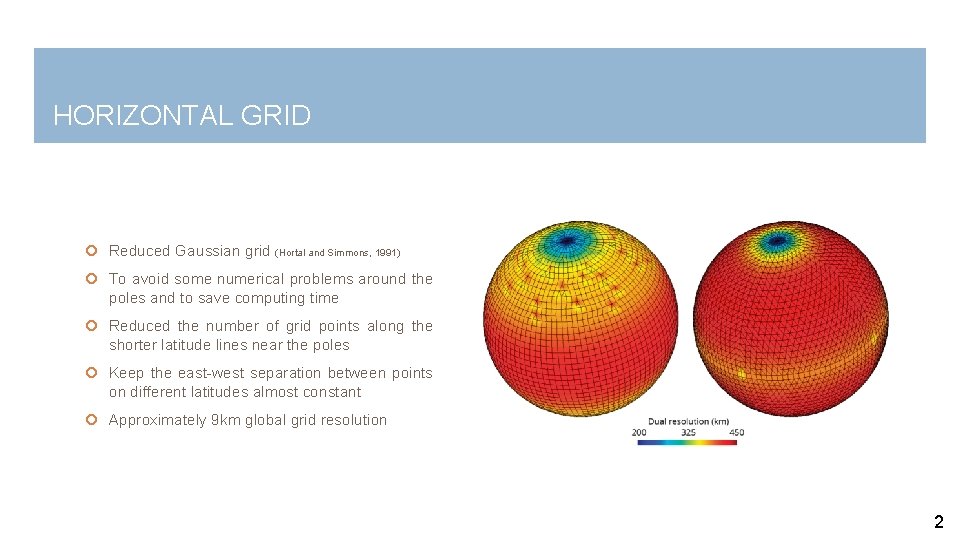
HORIZONTAL GRID Reduced Gaussian grid (Hortal and Simmons, 1991) To avoid some numerical problems around the poles and to save computing time Reduced the number of grid points along the shorter latitude lines near the poles Keep the east-west separation between points on different latitudes almost constant Approximately 9 km global grid resolution 2

VERTICAL GRID 3

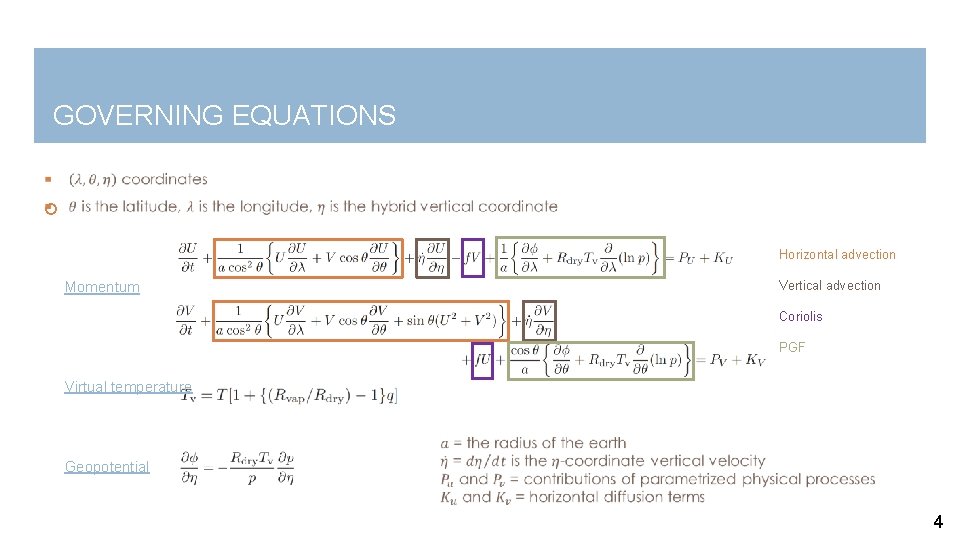
GOVERNING EQUATIONS Horizontal advection Momentum Vertical advection Coriolis PGF Virtual temperature Geopotential 4

GOVERNING EQUATIONS CONT. Thermodynamic Horizontal advection Vertical advection Moisture Continuity Adiabatic Horizontal gradient operator Vertical velocity in p coordinate Rate change of surface pressure Rate change of vertical velocity 5

VERTICAL DISCRETISATION The atmosphere is divided into NLEV layers to represent the variation of the dependent variables U, V, T and q The layers are defined by pressures at the interfaces between them The prognostic variables are represented by their values at “full-level” pressure pk The values of A and B are constants, define the vertical coordinate Rate change of ps Vertical advection of variable X Geopotential term Remaining of the PGF term Energy conversion term 6

TIME DISCRETISATION Semi-implicit correction term Momentum Thermodynamic Moisture 7

SEMI-LAGRANGIAN FORMULATION Local tendency Advection Linear Non-linear An explicit three-time-level semi-Lagrangian treatment is obtained by finding the approximate trajectory, over the time interval [t –Δt, t+Δt], of a particle which at each grid box x at time (t+Δt). +: arrival point (x, t+Δt) 0: the mid-point (x-α, t) -: the departure point (x-2α, t-Δt) 8

SEMI-LAGRANGIAN GOVERNING EQUATIONS Average between the values at departure and arrival point Momentum Thermodynamic Midpoint of the trajectory Moisture Continuity Midpoint of the trajectory 9

MODIFIED SEMI-LAGRANGIAN EQUATIONS Momentum equations The Coriolis terms can be incorporated in the semi-Lagrangian advection Continuity equation Spurious resonant response to steady orographic forcing Thermodynamic equation Depends on the underlying orography Spurious warming over mountain tops 10

IFS DOCUMENTATIONS Dynamics and numerical procedures https: //www. ecmwf. int/sites/default/files/elibrary/2017/17735 -part-iii-dynamics-and-numerical-procedures. pdf Physical processes https: //www. ecmwf. int/sites/default/files/elibrary/2017/17736 -part-iv-physical-processes. pdf Observations https: //www. ecmwf. int/sites/default/files/elibrary/2016/17733 -part-i-observations. pdf Ensemble prediction system https: //www. ecmwf. int/sites/default/files/elibrary/2017/17737 -part-v-ensemble-prediction-system. pdf Technical and computational procedures https: //www. ecmwf. int/sites/default/files/elibrary/2017/17738 -part-vi-technical-and-computational-procedures. pdf Data assimilation https: //www. ecmwf. int/sites/default/files/elibrary/2017/17734 -part-ii-data-assimilation. pdf ECMWF wave model https: //www. ecmwf. int/sites/default/files/elibrary/2017/17739 -part-vii-ecmwf-wave-model. pdf