ECECS 552 Arithmetic I Instructor Mikko H Lipasti

ECE/CS 552: Arithmetic I Instructor: Mikko H Lipasti Fall 2010 University of Wisconsin-Madison Lecture notes partially based on set created by Mark Hill.

Basic Arithmetic and the ALU l l l Number representations: 2’s complement, unsigned Addition/Subtraction Add/Sub ALU l Full adder, ripple carry, subtraction Carry-lookahead addition Logical operations l and, or, xor, nor, shifts Overflow

Basic Arithmetic and the ALU l Covered later in the semester: – Integer multiplication, division – Floating point arithmetic l These are not crucial for the project

Background l Recall – n bits enables 2 n unique combinations Notation: b 31 b 30 … b 3 b 2 b 1 b 0 l No inherent meaning l – f(b 31…b 0) => integer value – f(b 31…b 0) => control signals

Background l 32 -bit types include – Unsigned integers – Single-precision floating point – MIPS instructions (book inside cover)

Unsigned Integers l l f(b 31…b 0) = b 31 x 231 + … + b 1 x 21 + b 0 x 20 Treat as normal binary number E. g. 0… 0110101 = 1 x 27 + 1 x 26 + 0 x 25 + 1 x 24 + 1 x 23 + 0 x 21 + 1 x 20 = 128 + 64 + 16 + 4 + 1 = 213 l l l Max f(111… 11) = 232 – 1 = 4, 294, 967, 295 Min f(000… 00) = 0 Range [0, 232 -1] => # values (232 -1) – 0 + 1 = 232

Signed Integers l 2’s complement f(b 31…b 0) = -b 31 x 231 + … b 1 x 21 + b 0 x 20 Max f(0111… 11) = 231 – 1 = 2147483647 l Min f(100… 00) = -231 = -2147483648 (asymmetric) l l Range[-231, 231 -1] => # values(231 -1 - -231) = 232 l Invert bits and add one: e. g. – 6 – 000… 0110 => 111… 1001 + 1 => 111… 1010

Why 2’s Complement l l Why not use sign-magnitude? 2’s complement makes hardware simpler Just like humans don’t work with Roman numerals Representation affects ease of calculation, not correctness of answer 000 111 0 001 -1 1 110 -2 2 010 -3 3 -4 101 011 100 000 111 0 001 -3 1 110 -2 2 010 -1 3 -0 101 011 100

Addition and Subtraction l l 4 -bit unsigned example 0 1 0 0 1 1 1 0 3 10 1 13 4 -bit 2’s complement – ignoring overflow 0 1 1 0 0 1 1 1 0 1 3 -6 -3

Subtraction A – B = A + 2’s complement of B l E. g. 3 – 2 l 0 1 0 1 3 -2 1

Full Adder l l l Full adder (a, b, cin) => (cout, s) cout = two or more of (a, b, cin) s = exactly one or three of (a, b, cin) a 0 0 1 1 b 0 0 1 1 cin 0 1 0 1 cout 0 0 0 1 1 1 s 0 1 1 0 0 1

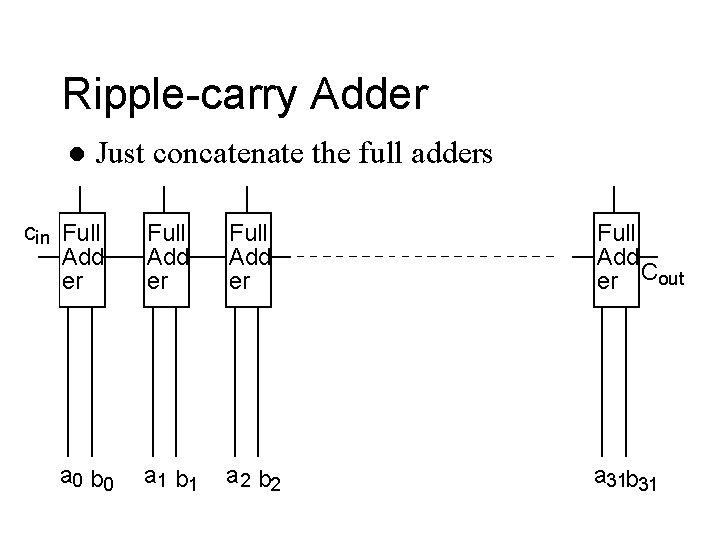
Ripple-carry Adder l Just concatenate the full adders cin Full Add er a 0 b 0 Full Add er Cout a 1 b 1 a 2 b 2 a 31 b 31

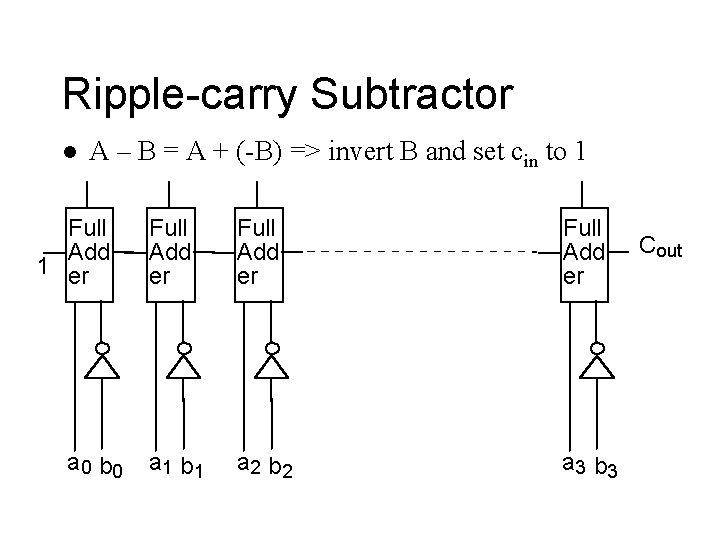
Ripple-carry Subtractor l A – B = A + (-B) => invert B and set cin to 1 Full Add 1 er a 0 b 0 Full Add er a 1 b 1 a 2 b 2 a 3 b 3 Cout

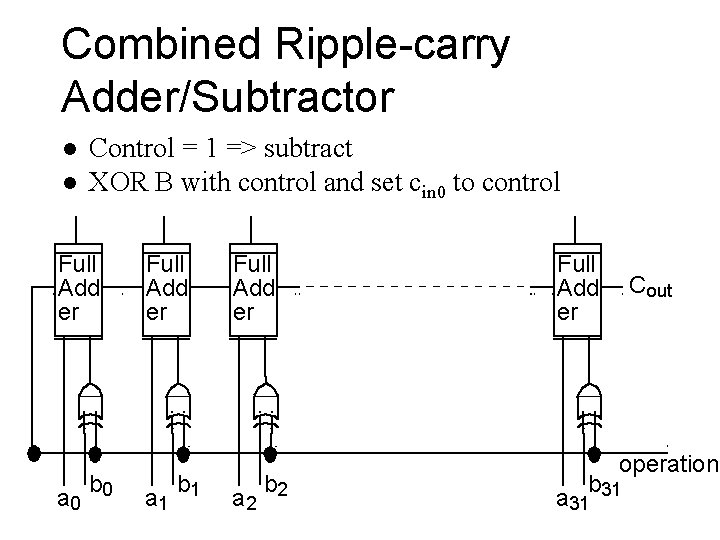
Combined Ripple-carry Adder/Subtractor l l Control = 1 => subtract XOR B with control and set cin 0 to control Full Add er a 0 b 0 Full Add er a 1 b 1 Full Add er a 2 b 2 Full Add er Cout operation b 31 a 31

Carry Lookahead l The above ALU is too slow – Gate delays for add = 32 x FA + XOR ~= 64 l Theoretically, in parallel – Sum 0 = f(cin, a 0, b 0) – Sumi = f(cin, ai…a 0, , bi…b 0) – Sum 31 = f(cin, a 31…a 0, b 31…b 0) l Any boolean function in two levels, right? – Wrong! Too much fan-in!

Carry Lookahead l Need compromise – Build tree so delay is O(log 2 n) for n bits – E. g. 2 x 5 gate delays for 32 bits l We will consider basic concept with – 4 bits – 16 bits l Warning: a little convoluted

Carry Lookahead 0101 0100 0011 0110 Need both 1 to generate carry and at least one to propagate carry Define: gi = ai * bi ## carry generate pi = ai + bi ## carry propagate Recall: ci+1 = ai * bi + ai * ci + bi * ci = ai * bi + (ai + bi) * ci = gi + pi * ci

Carry Lookahead l Therefore c 1 = g 0 + p 0 * c 0 c 2 = g 1 + p 1 * c 1 = g 1 + p 1 * (g 0 + p 0 * c 0) = g 1 + p 1 * g 0 + p 1 * p 0 * c 0 c 3 = g 2 + p 2 * g 1 + p 2 * p 1 * g 0 + p 2 * p 1 * p 0 * c 0 c 4 = g 3 + p 3*g 2 + p 3*p 2*g 1 + p 3*p 2*p 1*g 0 + p 3*p 2*p 1*p 0*c 0 l Uses one level to form pi and gi, two levels for carry l But, this needs n+1 fanin at the OR and the rightmost AND

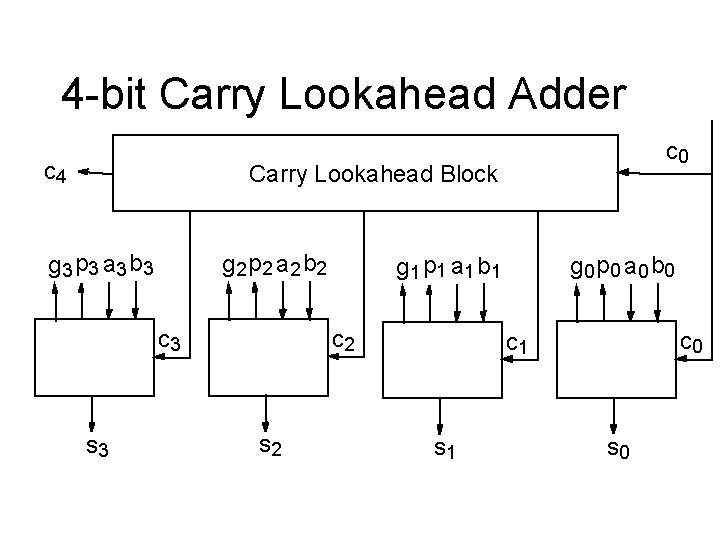
4 -bit Carry Lookahead Adder c 4 c 0 Carry Lookahead Block g 3 p 3 a 3 b 3 g 2 p 2 a 2 b 2 c 3 s 3 g 1 p 1 a 1 b 1 c 2 s 2 g 0 p 0 a 0 b 0 c 1 s 0

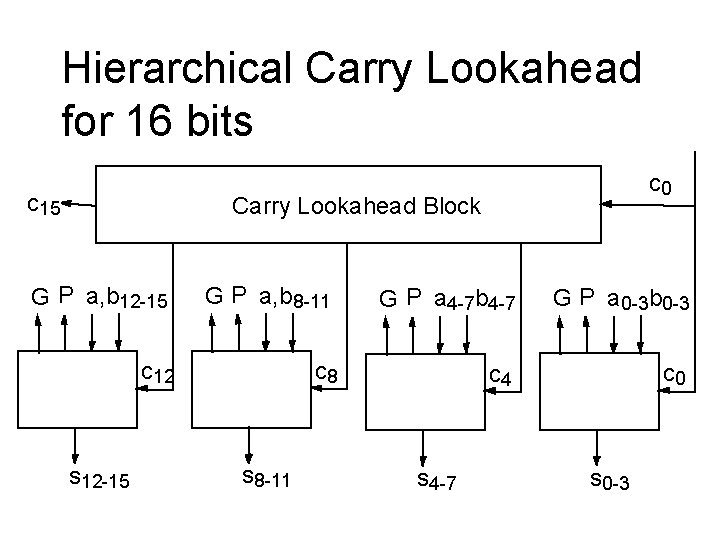
Hierarchical Carry Lookahead for 16 bits c 15 c 0 Carry Lookahead Block G P a, b 12 -15 G P a, b 8 -11 G P a 4 -7 b 4 -7 G P a 0 -3 b 0 -3 c 12 c 8 c 4 c 0 s 12 -15 s 8 -11 s 4 -7 s 0 -3

Hierarchical CLA for 16 bits Build 16 -bit adder from four 4 -bit adders Figure out G and P for 4 bits together G 0, 3 = g 3 + p 3 * g 2 + p 3 * p 2 * g 1 + p 3 * p 2 * p 1 * g 0 P 0, 3 = p 3 * p 2 * p 1 * p 0 (Notation a little different from the book) G 4, 7 = g 7 + p 7 * g 6 + p 7 * p 6 * g 5 + p 7 * p 6 * p 5 * g 4 P 4, 7 = p 7 * p 6* p 5 * p 4 G 12, 15 = g 15 + p 15 * g 14 + p 15* p 14 * g 13 + p 15 * p 14 * p 13 * g 12 P 12, 15 = p 15 * p 14 * p 13 * p 12

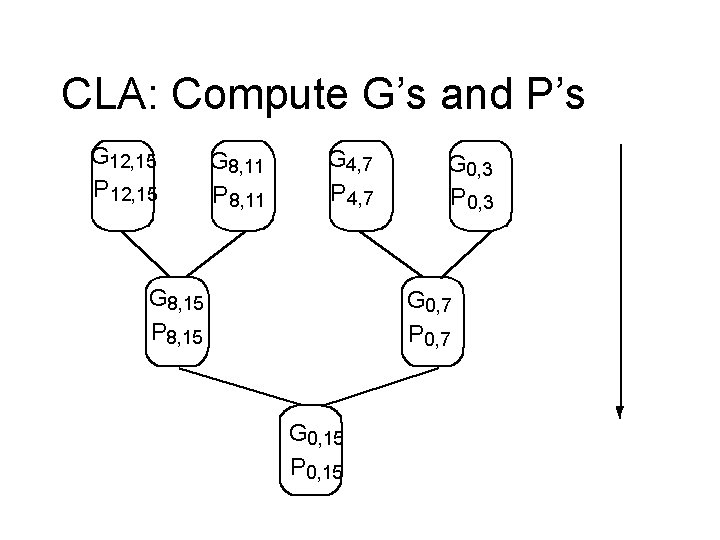
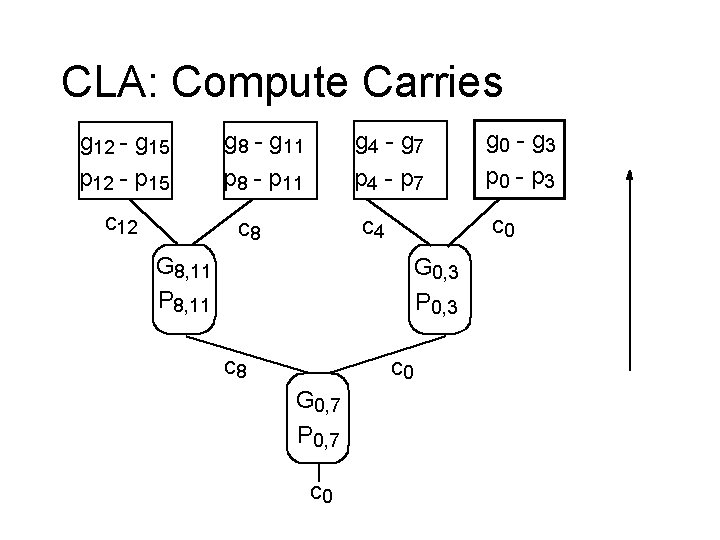
Carry Lookahead Basics Fill in the holes in the G’s and P’s Gi, k = Gj+1, k + Pj+1, k * Gi, j (assume i < j +1 < k ) Pi, k = Pi, j * Pj+1, k G 0, 7 = G 4, 7 + P 4, 7 * G 0, 3 P 0, 7 = P 0, 3* P 4, 7 G 8, 15 = G 12, 15 + P 12, 15 * G 8, 11 P 8, 15 = P 8, 11 * P 12, 15 G 0, 15 = G 8, 15 + P 8, 15 * G 0, 7 P 0, 15 = P 0, 7 * P 8, 15

CLA: Compute G’s and P’s G 12, 15 P 12, 15 G 8, 11 P 8, 11 G 4, 7 P 4, 7 G 8, 15 P 8, 15 G 0, 3 P 0, 3 G 0, 7 P 0, 7 G 0, 15 P 0, 15

CLA: Compute Carries g 12 - g 15 p 12 - p 15 c 12 g 8 - g 11 g 4 - g 7 p 8 - p 11 p 4 - p 7 c 0 c 4 c 8 G 8, 11 P 8, 11 G 0, 3 P 0, 3 c 8 c 0 G 0, 7 P 0, 7 c 0 g 0 - g 3 p 0 - p 3

Other Adders: Carry Select l Two adds in parallel; with and without cin – When Cin is done, select correct result Full Adder 0 Full Adder next select Full Adder 1 2 -1 Mux select c 0

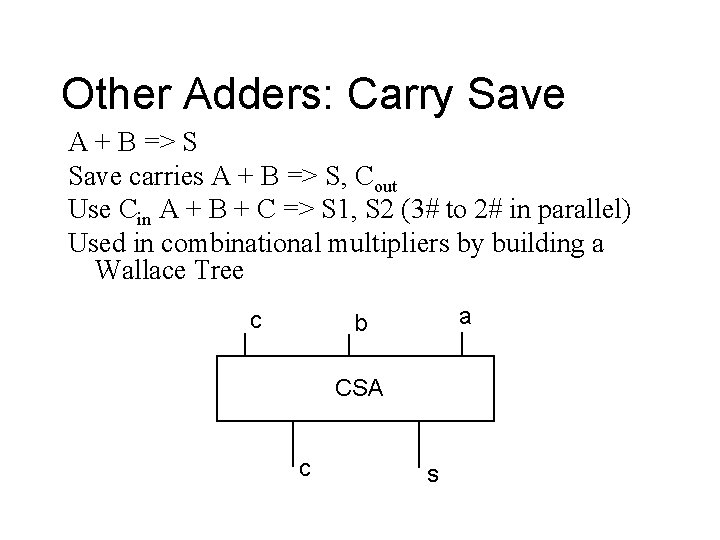
Other Adders: Carry Save A + B => S Save carries A + B => S, Cout Use Cin A + B + C => S 1, S 2 (3# to 2# in parallel) Used in combinational multipliers by building a Wallace Tree c a b CSA c s

Adding Up Many Bits f e d c CSA b a CSA S 0 CSA S 2 S 1

Logical Operations l Bitwise AND, OR, XOR, NOR – Implement w/ 32 gates in parallel l Shifts and rotates – – – rol => rotate left (MSB->LSB) ror => rotate right (LSB->MSB) sll -> shift left logical (0 ->LSB) srl -> shift right logical (0 ->LSB) sra -> shift right arithmetic (old MSB->new MSB)

Shifter

Shifter E. g. , Shift left logical for d<7: 0> and shamt<2: 0> Using 2 -1 Muxes called Mux(select, in 0, in 1) stage 0<7: 0> = Mux(shamt<0>, d<7: 0>, 0 || d<7: 1>) stage 1<7: 0> = Mux(shamt<1>, stage 0<7: 0>, 00 || stage 0<6: 2>) dout<7: 0) = Mux(shamt<2>, stage 1<7: 0>, 0000 || stage 1<3: 0>) For Barrel shifter used wider muxes

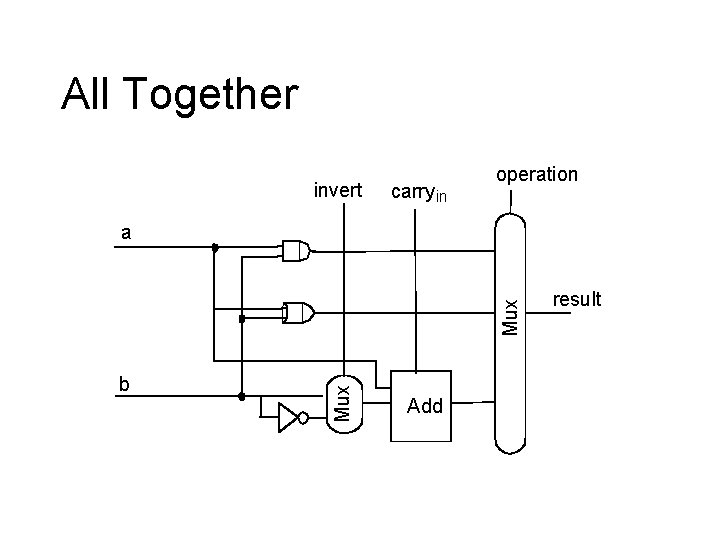
All Together invert carry in operation b Mux a Add result

Overflow With n bits only 2 n combinations l Unsigned [0, 2 n-1], 2’s complement [-2 n-1, 2 n-1 -1] l Unsigned Add 5 + 6 > 7: 101 + 110 => 1011 f(3: 0) = a(2: 0) + b(2: 0) => overflow = f(3) Carryout from MSB l

Overflow More involved for 2’s complement -1 + -1 = -2: 111 + 111 = 1110 = -2 is correct l Can’t just use carry-out to signal overflow l

Addition Overflow l When is overflow NOT possible? (p 1, p 2) > 0 and (n 1, n 2) < 0 p 1 + p 2 p 1 + n 1 not possible n 1 + p 2 not possible n 1 + n 2 l Just checking signs of inputs is not sufficient

Addition Overflow l 2 + 3 = 5 > 4: 010 + 011 = 101 =? – 3 < 0 – Sum of two positive numbers should not be negative l l Conclude: overflow -1 + -4: 111 + 100 = 011 > 0 – Sum of two negative numbers should not be positive l Conclude: overflow Overflow = f(2) * ~(a 2)*~(b 2) + ~f(2) * a(2) * b(2)

Subtraction Overflow No overflow on a-b if signs are the same l Neg – pos => neg ; ; overflow otherwise l Pos – neg => pos ; ; overflow otherwise l Overflow = f(2) * ~(a 2)*(b 2) + ~f(2) * a(2) * ~b(2)

What to do on Overflow? l Ignore ! (C language semantics) – What about Java? (try/catch? ) Flag – condition code l Sticky flag – e. g. for floating point l – Otherwise gets in the way of fast hardware l Trap – possibly maskable – MIPS has e. g. add that traps, addu that does not

Zero and Negative Zero = ~[f(2) + f(1) + f(0)] l Negative = f(2) (sign bit) l

Zero and Negative May also want correct answer even on overflow l Negative = (a < b) = (a – b) < 0 even if overflow l E. g. is – 4 < 2? l 100 – 010 = 1010 (-4 – 2 = -6): Overflow! l Work it out: negative = f(2) XOR overflow

Summary Binary representations, signed/unsigned l Arithmetic l – Full adder, ripple-carry, carry lookahead – Carry-select, Carry-save – Overflow, negative – More (multiply/divide/FP) later l Logical – Shift, and, or