ECE 665 Spring 2005 Computer Algorithms with Applications

ECE 665 Spring 2005 Computer Algorithms with Applications to VLSI CAD Linear Programming Duality – Longest Path Problem 1

Linear Program Dual – Example 1 • Primal LP (original) • Dual LP (original) max 100 x 1 + 80 x 2 s. to: 10 x 1 + 5 x 2 50 5 x 1 + 5 x 2 35 5 x 1 + 15 x 2 80 min 50 w 1 + 35 w 2 + 80 w 3 s. to: 10 w 1 + 5 w 2 + 5 w 3 100 5 w 1 + 5 w 2 + 15 w 3 80 Primal solution: x 1=3, x 2 =4, Fp = 620 max c. T x s. to: A x b x 0 w 1 w 2 w 3 Dual solution: w 1=4, w 2 =12, w 3=0 Fd = 620 max w. T b s. to: w. T A c. T w 0 2 ECE 665 - Longest Path dual

Example 2: Longest Path Problem • Formulate it as a Linear Program – Assign variables xi to each edge ei • xi = 1 if edge ei is in the longest path • xi = 0 otherwise – Write the objective function 1 x 1 4 2 x 3 2 x 2 5 x 4 4 2 3 – Write the constraint set x 7 5 x 6 x 5 2 5 x 8 3 3 x 9 6 6 3 ECE 665 - Longest Path dual

Example 2: Longest Path Problem (2) • Primal Problem max 4 x 1 st -x 1 - x 2 x 1 - x 4 x 2 + x 4 x 3 - x 6 x 5 + x 6 x 7 + x 8 + 5 x 2 + 2 x 3 + 2 x 4 + 2 x 5 + 3 x 6 + 5 x 7 + 3 x 8 + 6 x 9 + x 3 x 7 x 5 x 9 x 8 x 9 = = = end -1 0 0 1 1 x 1 4 2 x 2 5 x 4 x 3 2 4 2 3 x 5 x 6 x 7 5 2 5 x 8 3 3 x 9 6 6 4 ECE 665 - Longest Path dual

Example 2: Longest Path Problem (3) • Primal Problem - solution max 4 x 1 st -x 1 - x 2 x 1 - x 4 x 2 + x 4 x 3 - x 6 x 5 + x 6 x 7 + x 8 end + 5 x 2 + 2 x 3 + 2 x 4 + 2 x 5 + 3 x 6 + 5 x 7 + 3 x 8 + 6 x 9 + x 3 x 7 x 5 x 9 x 8 x 9 = = = -1 0 0 1 LP OPTIMUM FOUND AT STEP 4 2 2 x 4 VALUE 1. 000000 0. 000000 4 3 x 5 x 6 11. 000000 VARIABLE X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 x 2 5 x 3 2 2 OBJECTIVE FUNCTION VALUE 1) 1 x 1 REDUCED COST 0. 000000 1. 000000 0. 000000 3. 000000 2. 000000 0. 000000 3. 000000 x 7 5 2 5 x 8 3 3 x 9 6 6 5 ECE 665 - Longest Path dual

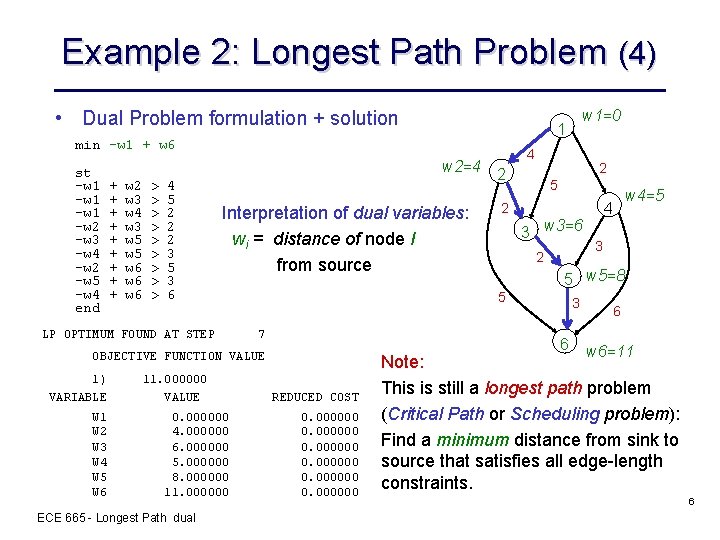
Example 2: Longest Path Problem (4) • Dual Problem formulation + solution min -w 1 + w 6 st -w 1 -w 2 -w 3 -w 4 -w 2 -w 5 -w 4 end w 2=4 + + + + + w 2 w 3 w 4 w 3 w 5 w 6 w 6 > > > > > 4 5 2 2 2 3 5 3 6 Interpretation of dual variables: wi = distance of node I from source LP OPTIMUM FOUND AT STEP W 1 W 2 W 3 W 4 W 5 W 6 11. 000000 VALUE 0. 000000 4. 000000 6. 000000 5. 000000 8. 000000 11. 000000 ECE 665 - Longest Path dual 2 2 5 REDUCED COST 0. 000000 4 2 3 w 3=6 2 w 4=5 3 5 w 5=8 3 6 OBJECTIVE FUNCTION VALUE 1) VARIABLE 4 5 7 w 1=0 1 6 w 6=11 Note: This is still a longest path problem (Critical Path or Scheduling problem): Find a minimum distance from sink to source that satisfies all edge-length constraints. 6