ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture

ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture 20 Multi-machine Dynamic Models Professor Pete Sauer Department of Electrical and Computer Engineering © 2000 University of Illinois Board of Trustees, All Rights Reserved

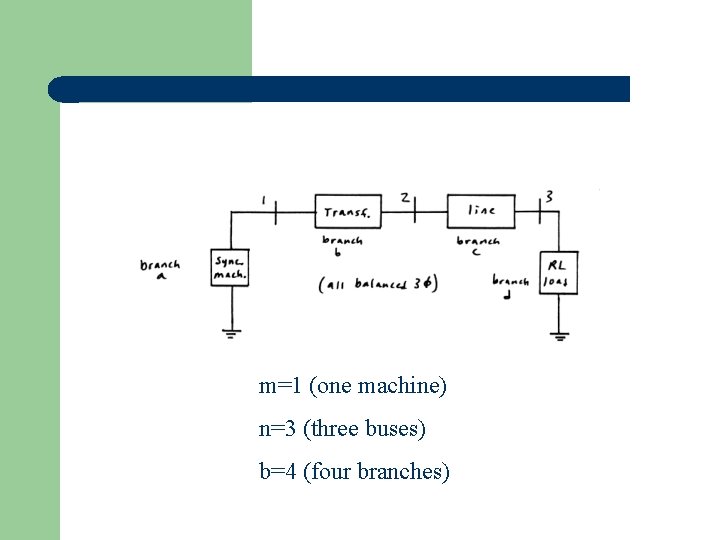
m=1 (one machine) n=3 (three buses) b=4 (four branches)

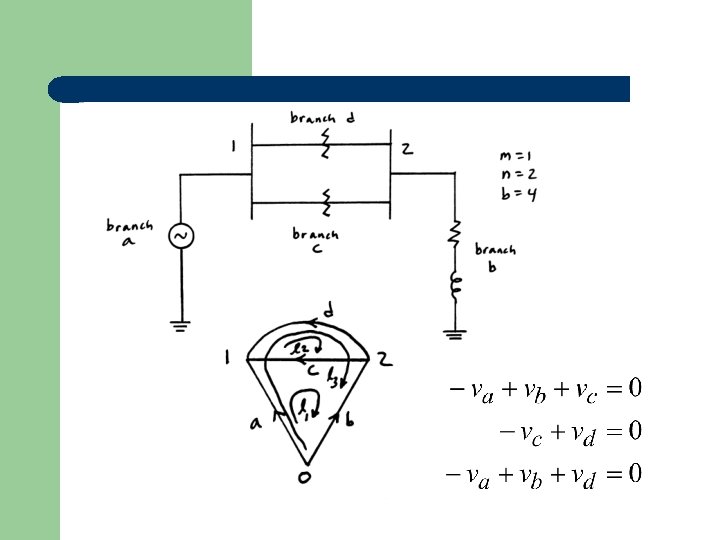
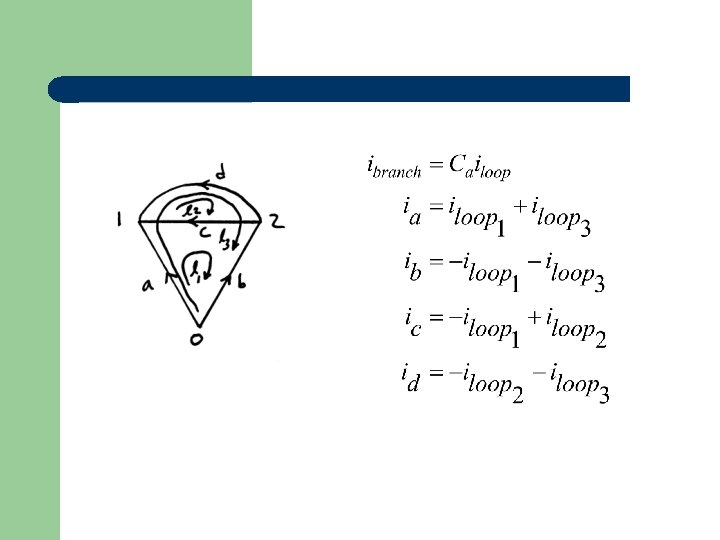
Branch-loop incidence matrix

b-n independent loops Systematically create independent loops: • Form a tree • Add b-n links to form b-n loops • This creates the “basic loop” matrix cb (b x b-n)

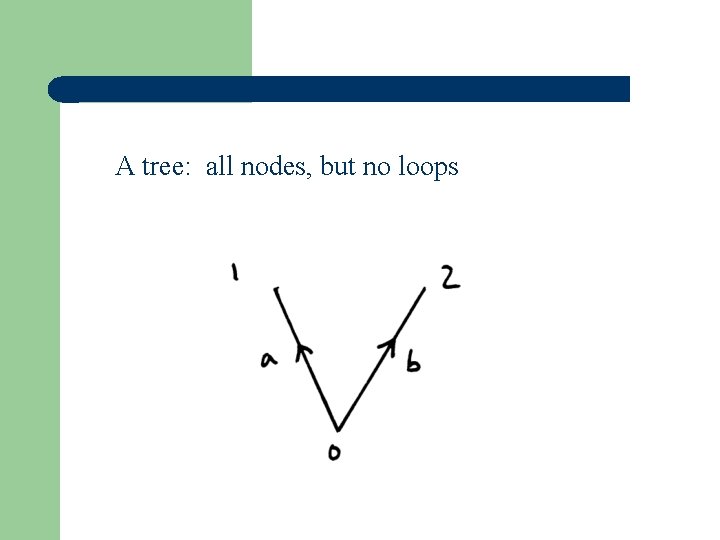
A tree: all nodes, but no loops

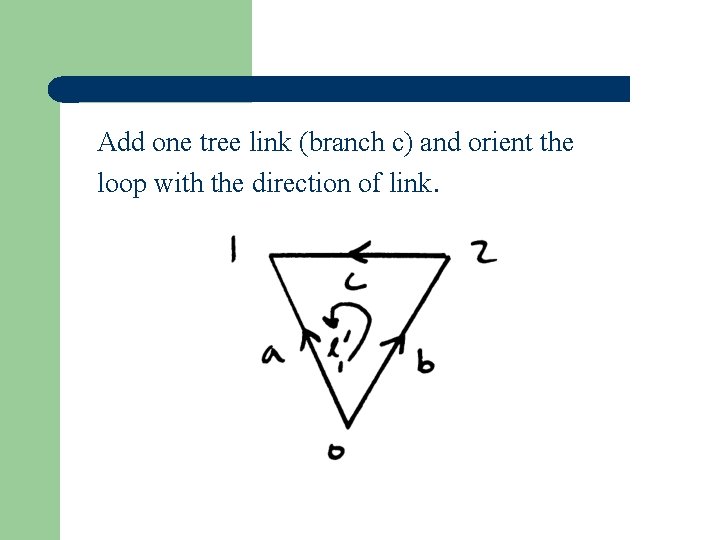
Add one tree link (branch c) and orient the loop with the direction of link.

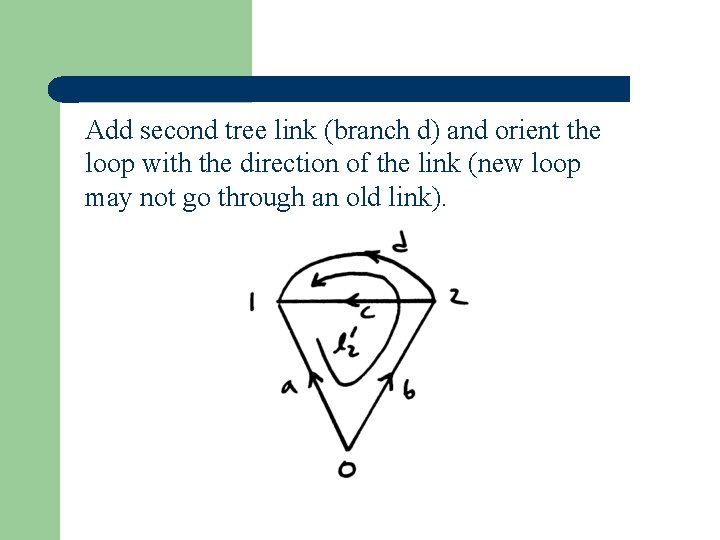
Add second tree link (branch d) and orient the loop with the direction of the link (new loop may not go through an old link).

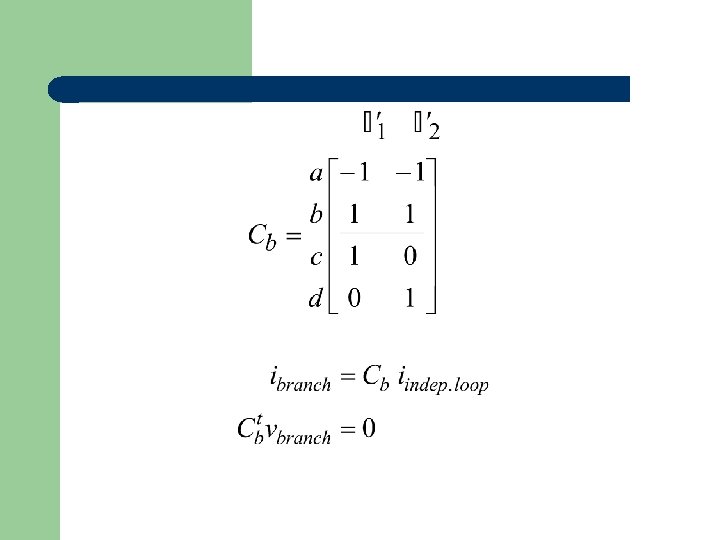
Define: (same for I and V) Define: (Independent loop flux linkages)

Then: (Independent loop currents) By our choice of numbering, the first m branches are machines and the last b-m branches are transformers, lines and loads.

Stator/network/load transients

Same for and V i=1, …. , m This if for b “disconnected” branches. Now connect them.

Multiply by and replace Ibranch by Cb. Iloop Note: If Rbranch=0, this is an exact integral manifold with:

Multi-machine quasi-steady state =0

Same for I, V

Sub-transient algebraic circuit

R-L elements

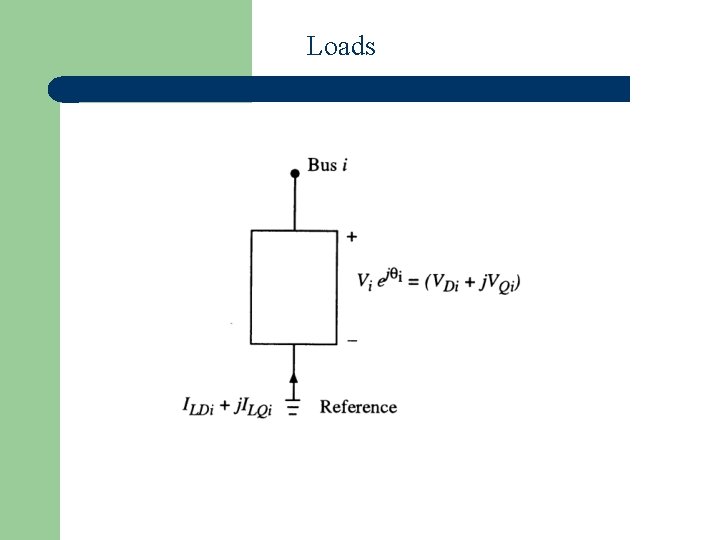
Loads

0, 1, 2 is the ZIP model