ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture

ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture 14 Damping torques and steady-state initial conditions Professor Pete Sauer Department of Electrical and Computer Engineering © 2000 University of Illinois Board of Trustees, All Rights Reserved

Damping torques 1. Friction and windage 2. Stator currents (load) 3. Field current (excitation) 4. Damper windings

Look for an integral manifold:


Substitute this into the torque equation. If the time constant is zero (zero-order integral manifold), you get the torque equation of the one-axis model. Since we are keeping the next term (first-order integral manifold), there is an additional torque term:

This can be approximated by a “constant D” damping torque term: That is: using a zero-order integral manifold does not capture any of the effects of the damper winding. However, a firstorder integral manifold does capture some of the damper winding effects.

Steady state Assume rated speed: Assume open circuit with no saturation. Assume the terminal voltage is 1. 0 per unit. Using the full model: The + and – come from the terminal voltage square root. Choose the positive solution


Apply resistive load Change: Id and Iq cannot change instantaneously but, Vd and Vq can. They will change from 0 and 1 to 0 and 0 when the resistive load is added. Could find the new steady state condition by integrating until things come to rest. What about an analytical steady-state solution?

New steady state (assuming it is stable). Using the full model, solve:

(With Vref given from the open-circuit solution)

(With Pc given from the open-circuit solution) (Assume TFW = 0)

20 equations in 20 unknowns – does the solution require iteration? After the solution is found, the angle delta is a time varying state: The steady-state value of delta cannot be found without integrating the full set of equations.

Recall the transformation back to abc and the definition of delta: The machine will have a new steady-state frequency.

General steady state when = s

Steady-state phasor diagram
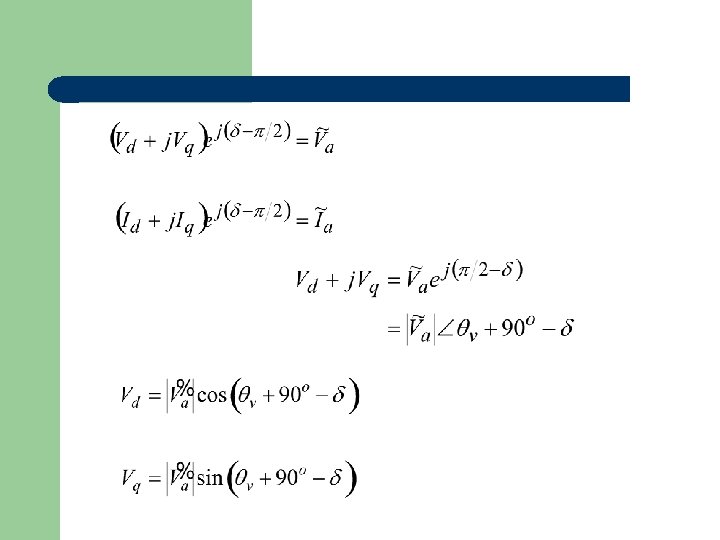

Example

Find: all synchronous machine dynamic states





Check:

(close to. 615)


- Slides: 30



















































