ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture

ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture 22 Interconnected Multi-Machine Model Professor M. A. Pai Department of Electrical and Computer Engineering © 2000 University of Illinois Board of Trustees, All Rights Reserved

Development of DAE Model l l Dynamic Equations of Machines and Exciter Algebraic Equations of Stator Algebraic Equations of Network Interconnection of the above to form a D. A. E model. of the form x = f (x, y) o = g (x, y) D. A. E. Differential - Algebraic Equations Lecture 22 – Page 1

Model Components Dynamic Components 1. Synchronous Machine (4 states) 2. Exciter (3 states) Algebraic components 1. Stator Algebraic Equations (2 for each machine) 2. Transmission Network Equations (2 for each bus) Power Balance or Current Balance Form. For an m machine, n bus network, we have (4 + 3)m=7 m d. e’s and (2 m + 2 n) algebraic equations. Typical m=100, n=10, 000 700 D. E & 20, 200 A. E Lecture 22 – Page 2

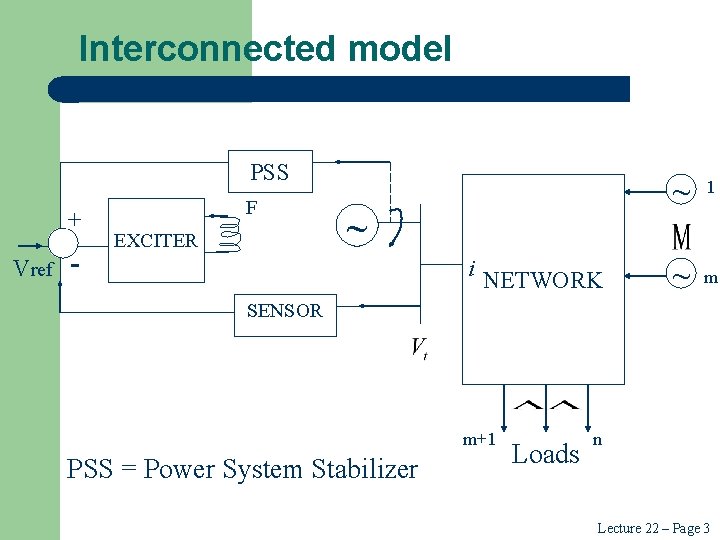
Interconnected model PSS + Vref - F EXCITER ~ i NETWORK ~ 1 ~ m SENSOR m+1 PSS = Power System Stabilizer Loads n Lecture 22 – Page 3

Nomenclature & their Units (Two Axis Model) Direct axis transient reactance (p. u. ) Quadrature axis transient reactance (p. u. ) are steady state reactances in direct and quadrature axis respectively (p. u. ) Field winding time constant (sec) Damper winding time constant (sec) Voltage proportional to field flux (p. u. ) Voltage proportional to damper flux in quadrature axis (p. u. ) Stator currents in machine reference frame(p. u. ) Inertia constant (secs) Motor angle (radians) Angular velocity (radians/sec) Lecture 22 – Page 4

Synchronous Machine (Differential Equations) Note (1) We assume as constant input. (2) (3) Zero Mechanical Damping Lecture 22 – Page 5

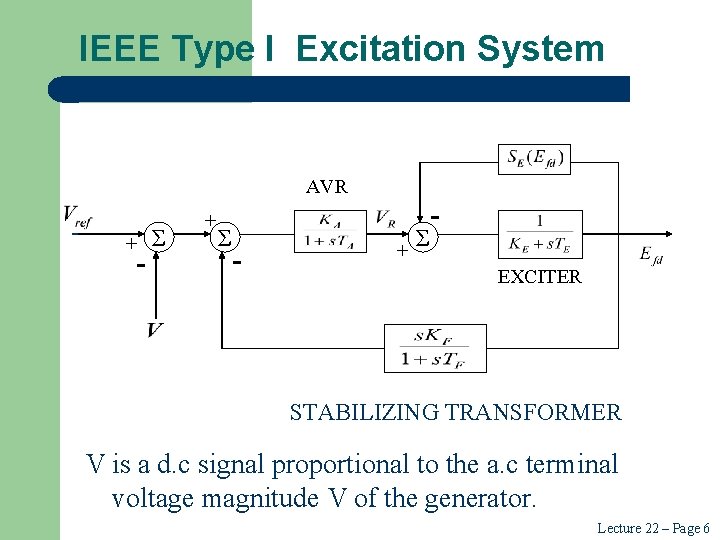
IEEE Type I Excitation System AVR - Σ Σ - + + - + Σ EXCITER STABILIZING TRANSFORMER V is a d. c signal proportional to the a. c terminal voltage magnitude V of the generator. Lecture 22 – Page 6

Differential Equations of Exciter is the reference input. Lecture 22 – Page 7

Stator Algebraic Equations + + - Write KVL to get the equation in Complex Notation Lecture 22 – Page 8

Stator Algebraic Equations (contd) Multiply by Imaginary Parts. and Equate Real and Lecture 22 – Page 9

Stator Algebraic Equations (contd) We can express 2 x 2 matrix: , explicitly by defining a Then, Symbolically in Polar Form, is a State Vector. , are Algebraic Variables. Lecture 22 – Page 10

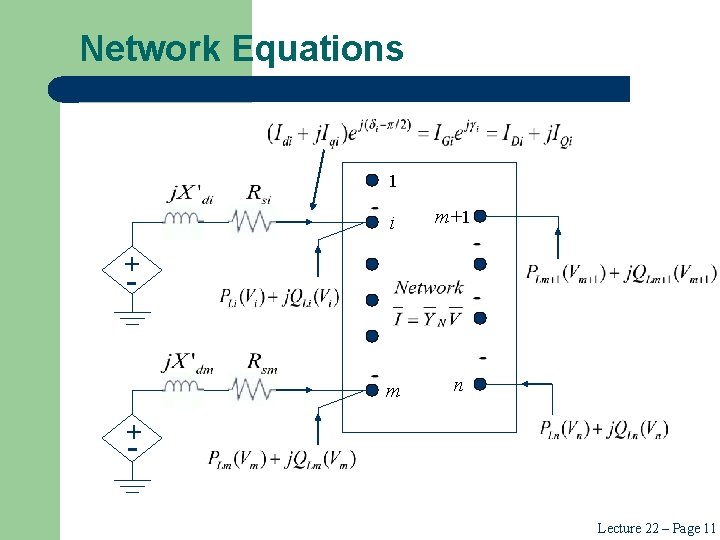
Network Equations 1 i m+1 m n + - Lecture 22 – Page 11

Network Equations (contd) Power Balance Form are the elements of the matrix. Lecture 22 – Page 12

Network Equations (contd) is the complex power “injected” into bus i due to the generator. Lecture 22 – Page 13

Separate Real and Imaginary Parts of Network Equations Real Power Equations Reactive Power Equations Lecture 22 – Page 14

Differential Algebraic Equation (DAE) Model We have 7 m+2 m+2 n equations with as the state vector where as the state vector for each machine. Let y is the algebraic set of variables. Lecture 22 – Page 15

DAE Model (contd) DAE model can be split as: Plug (2) in (1) and (3) to get: has dimensions of power and are in Polar Form. Lecture 22 – Page 16

Numerical example 1 ~ 2 ~ SLACK P-V 3 P-Q The state equations depend on the model that is used. Lecture 22 – Page 17

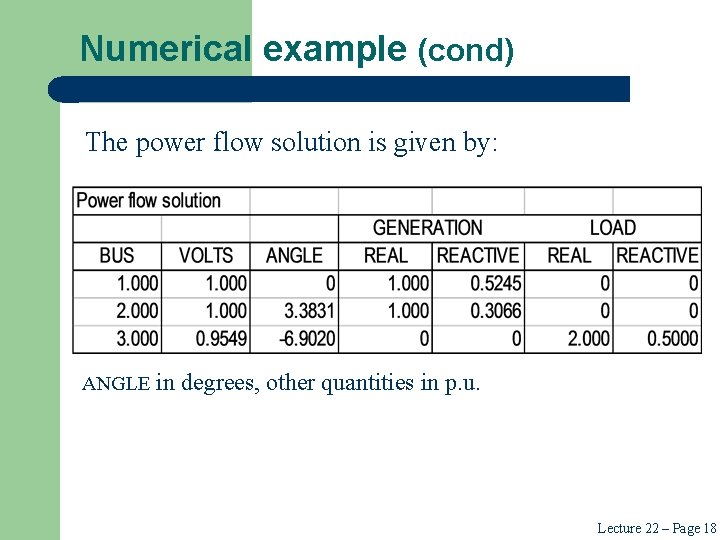
Numerical example (cond) The power flow solution is given by: ANGLE in degrees, other quantities in p. u. Lecture 22 – Page 18

Numerical example (cond) Stator Algebraic Equations (Assuming ) Lecture 22 – Page 19

Numerical example (cond) Network Equations Real power equations: (1) and (2) at Gen Buses, (3) P-Q Bus Lecture 22 – Page 20

Numerical example (cond) Reactive Power Equations: We then have equations in the form: Lecture 22 – Page 21