ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture

ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture 1 Introduction and Overview Professor Pete Sauer Department of Electrical and Computer Engineering © 2018 University of Illinois Board of Trustees, All Rights Reserved

Spring 2018 Instructors Pete Sauer University of Illinois at Urbana-Champaign Department of Electrical and Computer Eng. 4046 ECEB, 306 N. Wright St. , Urbana, IL 61801 (217) 333 -0394 psauer@illinois. edu Periodic substitution by: Karl Reinhard 4054 ECEB, 306 N. Wright St. , Urbana, IL 61801 reinhrd 2@illinois. edu

Power Systems • Aircraft • Automobiles • Standby power sources • Electric utilities • Mechanical prime movers • Electrical generators • Electrical network • Electrical loads

Dynamics and Stability Engineering analysis a) static – steady state b) dynamic – transients Stability – study of system response to disturbance

Course Topics 1. Structures 2. EMTP 3. Synchronous machine 4. Controls 5. Single machine 6. Simulation 7. Multi-machine 8. Simulation 9. Steady-state stability 10. Transient Stability

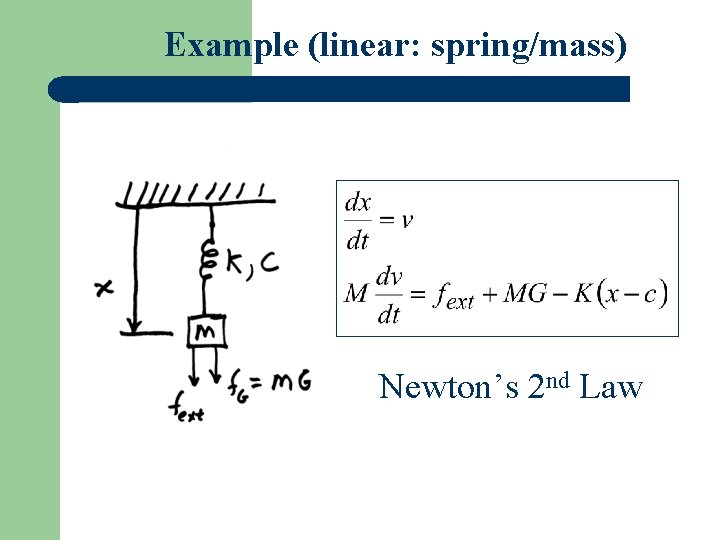
Example (linear: spring/mass) Newton’s 2 nd Law

a) Equilibrium Set time derivatives to zero Solve for dynamic states

b) Stability Suppose mass is displaced from xe. Will it return? Look at the D. E. (v goes negative) so x decreases (Tends to return to xe)

(v goes positive) so x increases (Tends to return to xe) Intuitive conclusion: system is stable at xe

c) Response K = 20 N/m M = 0. 1 kg C = 0. 1 m G = 9. 8 m/sec 2 Suppose fext = 0 N This gives ve = 0 xe = 0. 149 m What happens if x = 0. 149 m (at rest) and fext is changed to 0. 5 N at t = 0?

Solve:

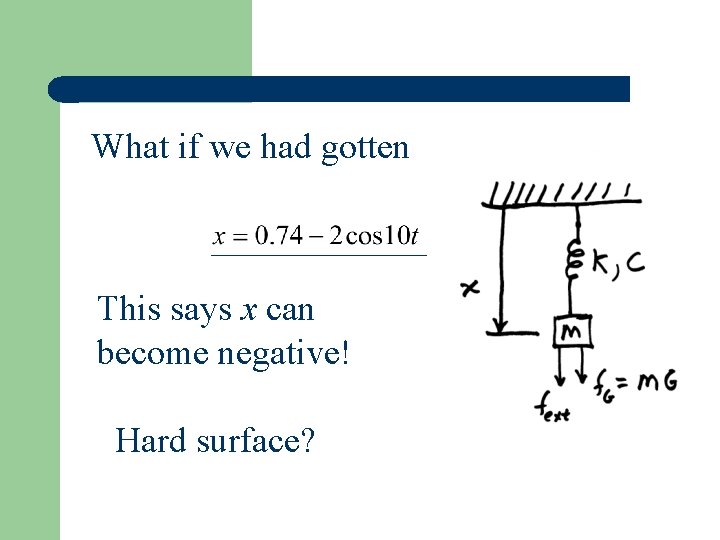
What if we had gotten ______ This says x can become negative! Hard surface?

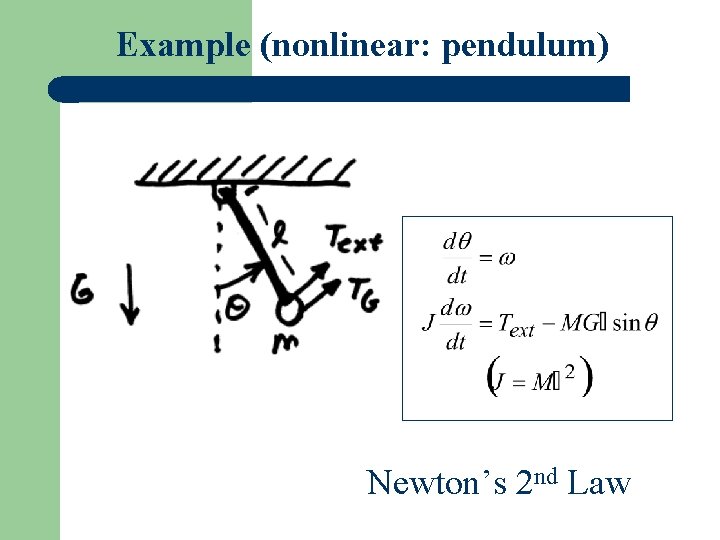
Example (nonlinear: pendulum) Newton’s 2 nd Law

a) Equilibrium Set time derivatives to zero (multiple values)

b) Stability Suppose mass is displaced. Will it return to e? Look at D. E. Consider e = 0 ( goes negative) ( decreases) (Tends to go back to e)

( goes positive) ( increases) (Tends to go back to e) Intuitive conclusion: e = 0 is a stable equilibrium point

Now try: ( goes positive) increases (Tends to go away from e)

( goes negative) decreases (Tends to go away from e) Intuitive conclusion: is an unstable equil. pt.

c) Response Suppose is at e = 0 ( e = 0) and Text is changed. What will happen? M = 0. 1 kg l = 1 m G = 9. 8 m/sec 2 Add Text = 0. 5 NM at t = 0

Numerical Integration Basic Idea: Taylor Series t small

Euler’s Forward method: t small

Choose t =. 01 sec

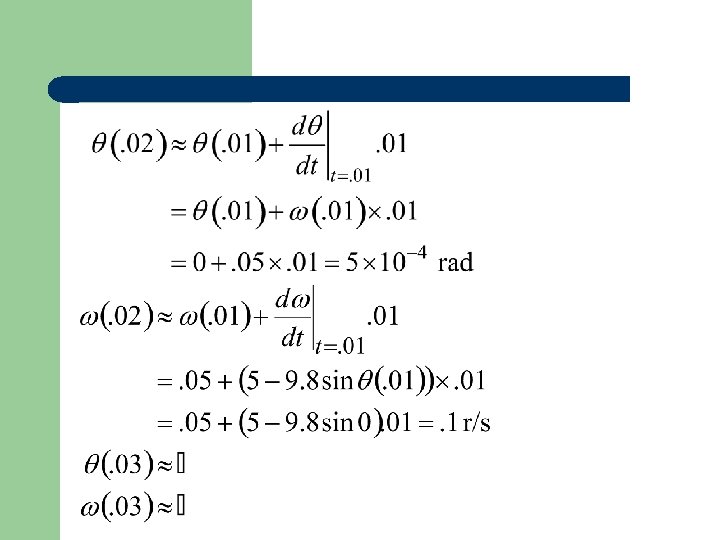
Tutorial demo The following demonstration software was created for a tutorial on nonlinear dynamics given for Union Electric (Ameren) with funding provided by EPRI in 1993