ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture

ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture 27 Reduced Order Multi-Machine Models Professor M. A. Pai Department of Electrical and Computer Engineering © 2000 University of Illinois Board of Trustees, All Rights Reserved
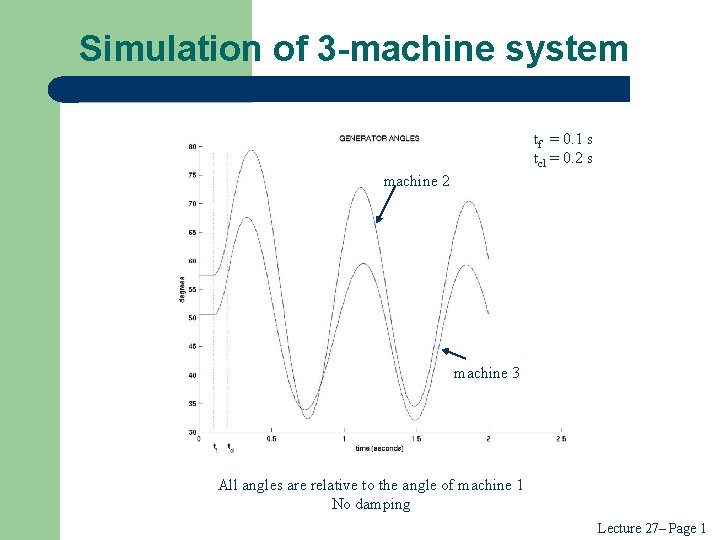
Simulation of 3 -machine system tf = 0. 1 s tcl = 0. 2 s machine 2 machine 3 All angles are relative to the angle of machine 1 No damping Lecture 27– Page 1
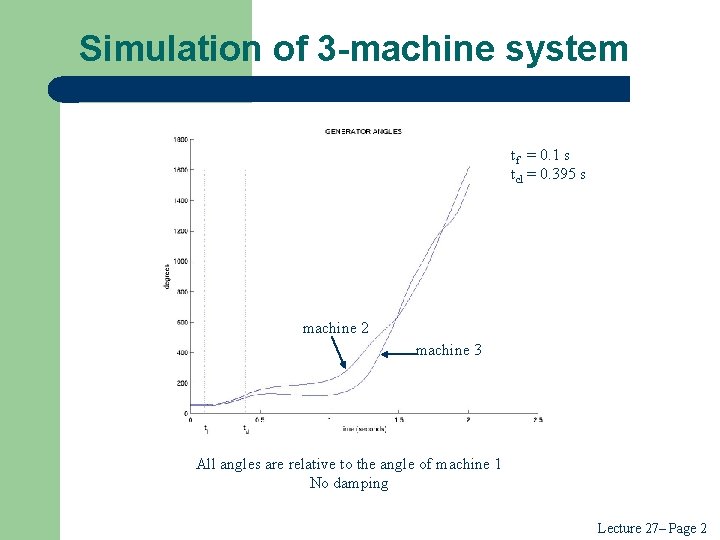
Simulation of 3 -machine system tf = 0. 1 s tcl = 0. 395 s machine 2 machine 3 All angles are relative to the angle of machine 1 No damping Lecture 27– Page 2
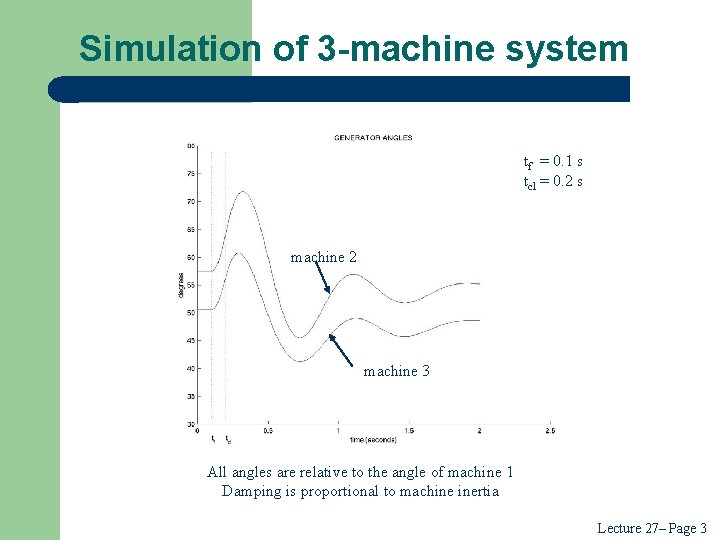
Simulation of 3 -machine system tf = 0. 1 s tcl = 0. 2 s machine 2 machine 3 All angles are relative to the angle of machine 1 Damping is proportional to machine inertia Lecture 27– Page 3
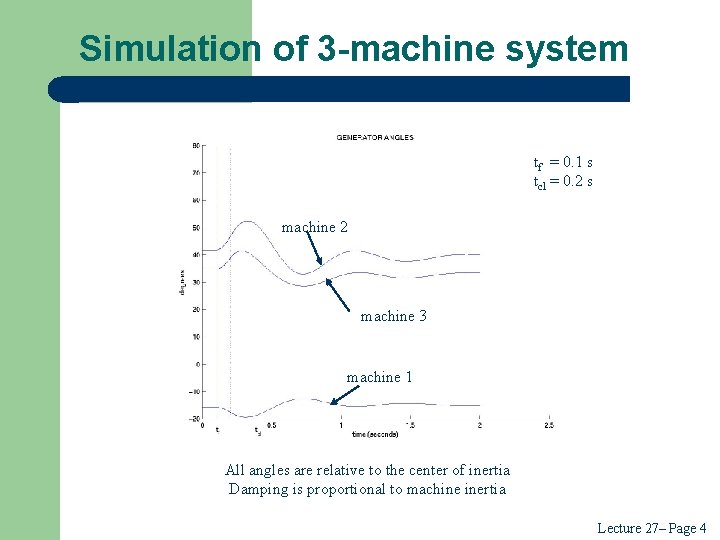
Simulation of 3 -machine system tf = 0. 1 s tcl = 0. 2 s machine 2 machine 3 machine 1 All angles are relative to the center of inertia Damping is proportional to machine inertia Lecture 27– Page 4

Reduced Order Models 1. 2. 3. Flux Decay Model (DAE) Classical Model (DAE Structure Preserving) (constant voltage behind transient reactance) Classical Model (DE only) (internal node model –network nodes eliminated) l (1) is popular in small signal analysis, oscillations l and their stabilization. (2) & (3) are popular in direct methods of stability analysis Lecture 27– Page 5

Flux decay model l l Damper winding constant is small Use of Singular Perturbation (integral manifold) makes the equation algebraic Substitute in Torque Eqn and Stator Algebraic Eqn l STATIC EXCITER Lecture 27– Page 6

Flux Decay Model (Stator Eqns) DYNAMIC CIRCUIT Stator Equations (Assume ) These are in polar form. Lecture 27– Page 7

Flux Decay Model (Generator Eqns) Generator Equations Network Equations: same as in previous DAE model Total number of equations 4 m + 2 n D. E Stator Network Lecture 27– Page 8

Classical Model of Machine l l More assumptions… is large i. e. is a slow variable and remains constant at initial value. simplifies stator and torque equations. Generator Equations l Will simplify later. Lecture 27– Page 9

Classical Model Derivation Stator Equations Would like to have voltage behind . Lecture 27– Page 10

Classical Model (contd) voltage behind transient reactance o No machine variables and no stator equations! = constant and computed as follows: Lecture 27– Page 11

Classical Model (contd) Step 1: From the load flow, compute Step 2: Compute is kept constant. appears in torque equation (page 5)and we need to compute it in terms of state and network variables. Lecture 27– Page 12

Classical Model (contd) Reactance does not consume real power. Hence, After expanding and simplifying (5) Lecture 27– Page 13
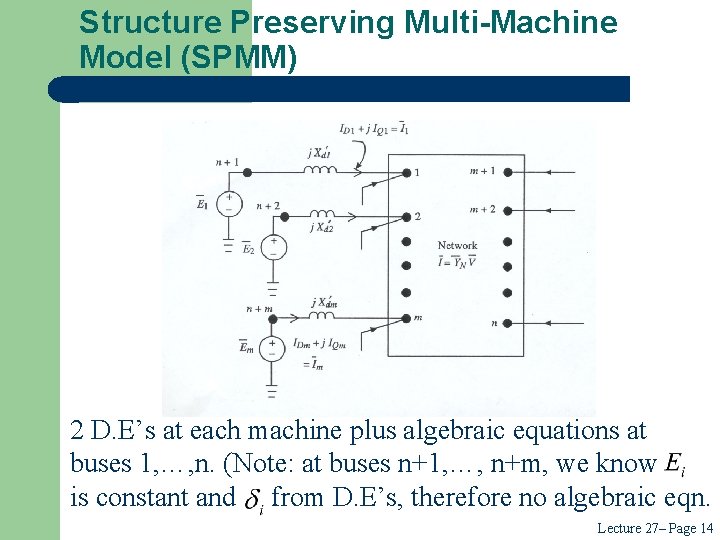
Structure Preserving Multi-Machine Model (SPMM) 2 D. E’s at each machine plus algebraic equations at buses 1, …, n. (Note: at buses n+1, …, n+m, we know is constant and from D. E’s, therefore no algebraic eqn. Lecture 27– Page 14

Structure Preserving Model At the generator buses i=1, …, m Lecture 27– Page 15
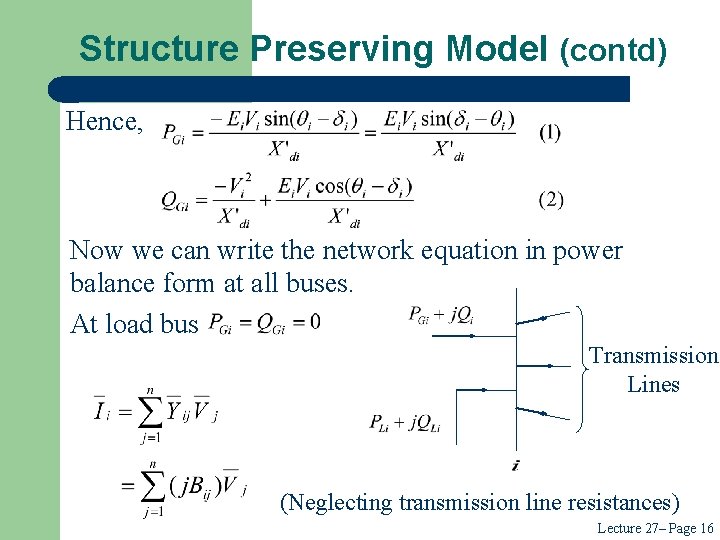
Structure Preserving Model (contd) Hence, Now we can write the network equation in power balance form at all buses. At load bus Transmission Lines (Neglecting transmission line resistances) Lecture 27– Page 16

Structure Preserving Model (contd) The total complex power in the network transmission lines from bus i is: Lecture 27– Page 17

Structure Preserving Model (contd) The network power balance equations are: Lecture 27– Page 18

Structure Preserving Model (contd) The D. E’s are: Plus the algebraic equations. Symbolically: Lecture 27– Page 19

Numerical example (2 machine system) 1 2 ~ ~ 3 Lecture 27– Page 20

Numerical example (2 machine system) Flux decay model: Lecture 27– Page 21

Numerical example (2 machine system) Lecture 27– Page 22

Numerical example (2 machine system) Classical model: Lecture 27– Page 23
- Slides: 24