ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture

ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture 33 Power System Stabilizers (PSS) Professor M. A. Pai Department of Electrical and Computer Engineering © 2000 University of Illinois Board of Trustees, All Rights Reserved

Functions of a PSS l l l PSS adds a signal to the excitation system proportional to speed deviation. This adds positive damping. Signal is generated locally from the shaft. Both local mode and inter-area mode can be damped. When oscillation is observed on a system or a planning study reveals poorly damped oscillations, use of participation factors helps in identifying the machine(s) where PSS has to be located. Tuning of PSS regularly is important. Modal Analysis technique forms the basis for multimachine systems. Lecture 33 – Page 1

Basic Approach DAE Model Linearizing about an operating point PSS principles are best understood for a single machine infinite bus (SMIB) system. Lecture 33 – Page 2

SMIB System (Flux Decay Model) Flux Decay Model and Fast Exciter ~ How are computed for a multi-machine system? Lecture 33 – Page 3

Computation of l Suppose at generator i we wish to obtain l Consider rest of the machines as infinite buses with voltages fixed. l From the physical terminal of generator i, obtain a Thevenin equivalent (i. e. short circuit all other generators and do network reduction) to get l This can be repeated for all other generators to get the SMIB equivalents. Lecture 33 – Page 4

Stator Equations Assume Stator Algebraic Equations are: Lecture 33 – Page 5

Network Equations The network equation is (assuming zero phase angle at the infinite bus and no local load) Simplifying, ~ Lecture 33 – Page 6

Complete SMIB Model Machine Stator equations Network equations ~ Lecture 33 – Page 7

Linearization of SMIB Model Lecture 33 – Page 8

Linearization (contd) Final Steps involve 1. Linearizing Machine Equations 2. Substitute (1) in the linearized equations of (2). Lecture 33 – Page 9

Linearization of Machine Equations Symbolically we have Substitute (3) in (2) to get linearized model. Lecture 33 – Page 10

Linearized SMIB Model Excitation system is yet to be included. K 1 – K 4 constants are: Lecture 33 – Page 11

K 1 – K 6 Constants K 1 – K 4 only involve machine and not the exciter. Lecture 33 – Page 12

Computing Before linearizing exciter equations, compute is an algebraic variable in the Excitation System. Lecture 33 – Page 13

Computing While linearizing stator algebraic equations, we had Substitute this in expression for to get We thus have K 1 – K 6 constant. Next construct the Heffron – Philips model. Lecture 33 – Page 14

Heffron – Phillips Model Add a fast exciter Linearize This together with Gives SMIB Model Lecture 33 – Page 15

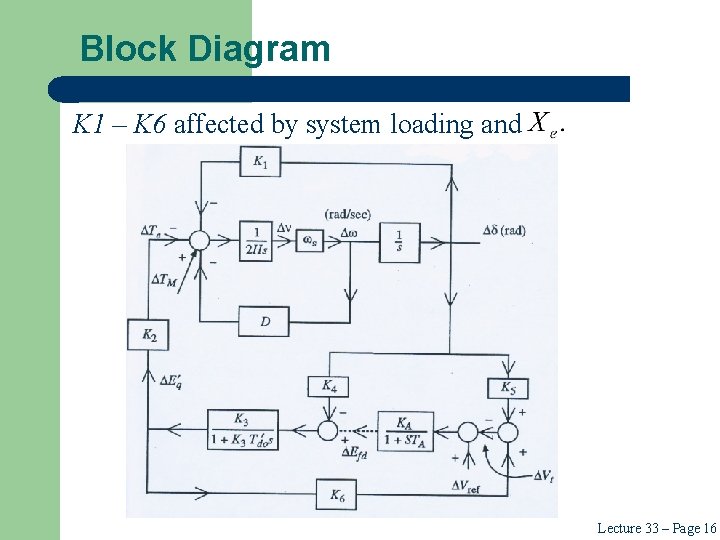
Block Diagram K 1 – K 6 affected by system loading and Lecture 33 – Page 16

Numerical Example Initial conditions ~ Lecture 33 – Page 17

Initial Conditions (contd) From the stator algebraic equation, Lecture 33 – Page 18

Initial Conditions (contd) From non linear model, setting derivatives = 0, This completes the calculation of the initial conditions. Lecture 33 – Page 19

Computation of K 1 – K 6 Constants The formulas are used. Lecture 33 – Page 20

Effect of Field Flux on System Stability With constant field voltage, , from block diagram are usually positive. For low frequencies and in steady state, Field flux variation due to feedback. (Armature reaction) introduces negative synchronizing torque. Lecture 33 – Page 21

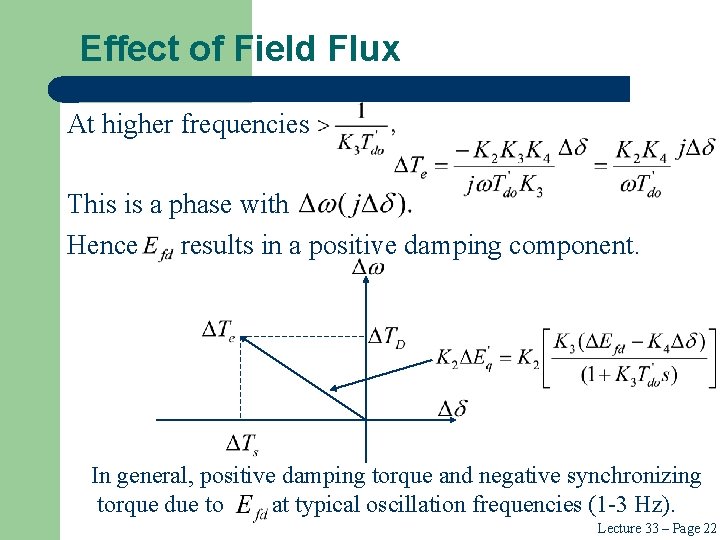
Effect of Field Flux At higher frequencies This is a phase with Hence results in a positive damping component. In general, positive damping torque and negative synchronizing torque due to at typical oscillation frequencies (1 -3 Hz). Lecture 33 – Page 22

Effect of Field Flux There are situations when can become negative. Case 1. A hydraulic generator without damper winding, light load ( is small) and connected to a line with high ratio and large system. Case 2. Machine is connected to a large local load, supplied partly by generator and partly by remote large system. If , damping due to is negative Lecture 33 – Page 23

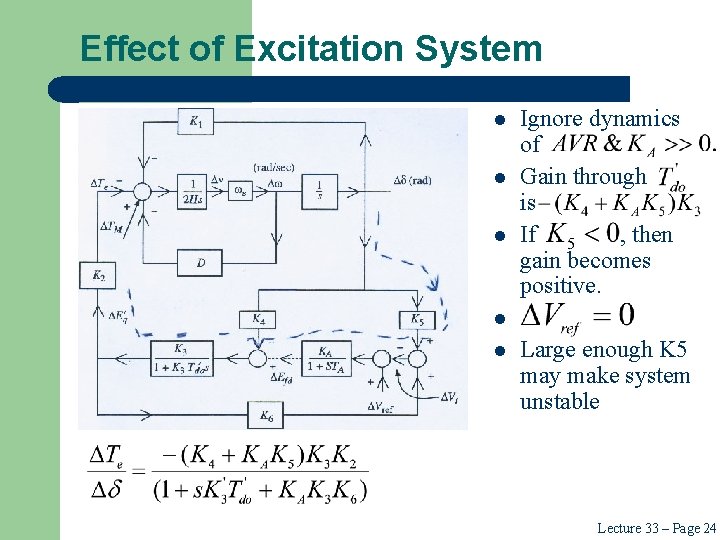
Effect of Excitation System l l l Ignore dynamics of Gain through is If , then gain becomes positive. l l Large enough K 5 may make system unstable Lecture 33 – Page 24

Numerical Example (Effect of Test system 1 ) Test System 2 Eigen Values Test System 1 Test System 2 unstable Lecture 33 – Page 25