ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture

ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture 13 Reduced-Order Synchronous Machine Models Professor Pete Sauer Department of Electrical and Computer Engineering © 2000 University of Illinois Board of Trustees, All Rights Reserved

Two-axis model

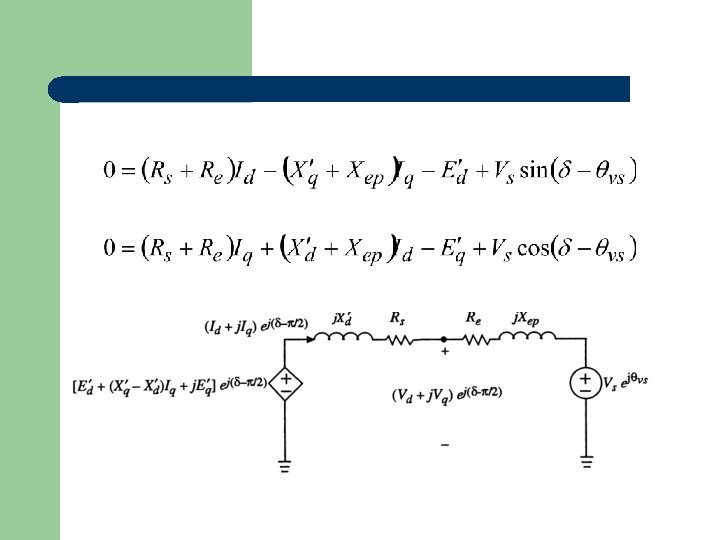
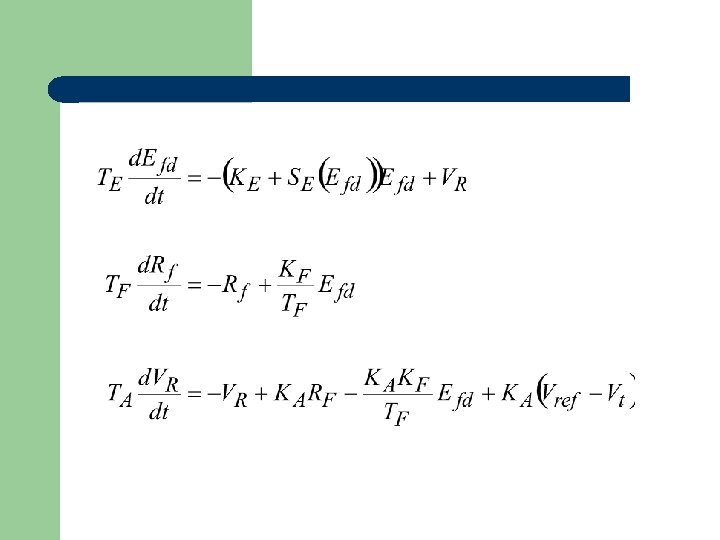
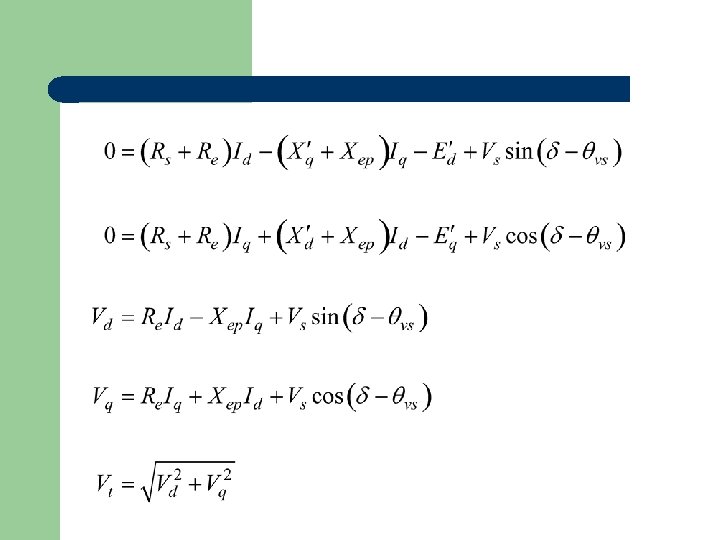
Flux-decay model

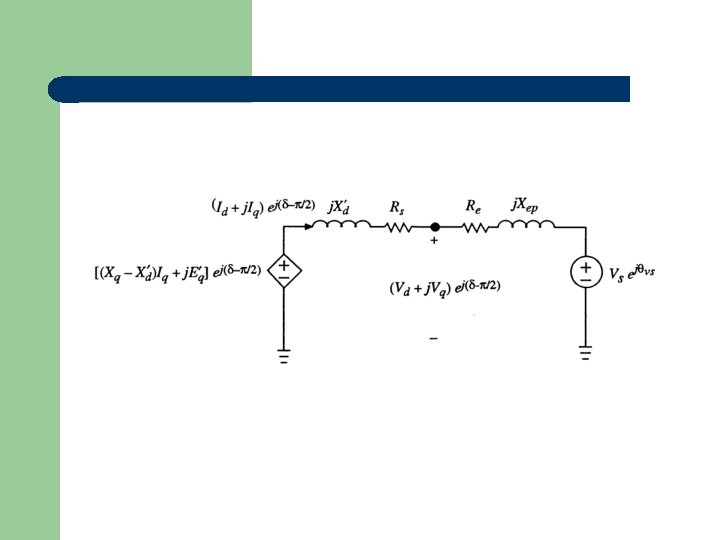
Classical model Or, go back to the two-axis model and assume:

Or, argue that an integral manifold exists for such that

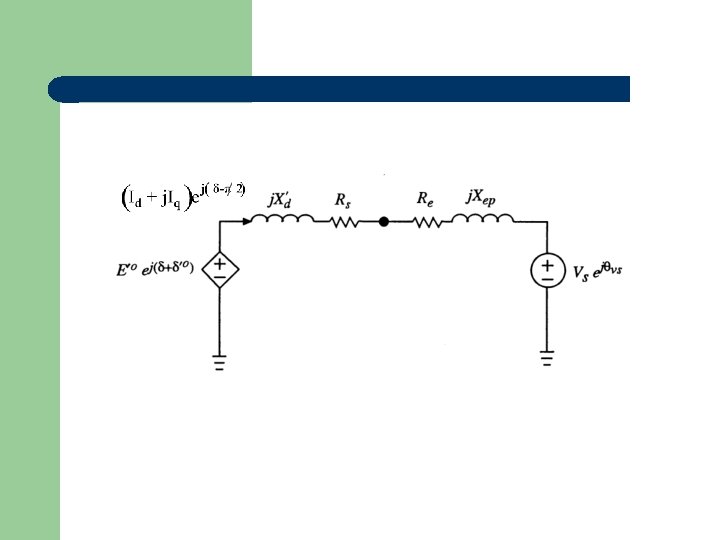
Neglect resistance and assume TCH = ∞ This is a pendulum model

Summary of 5 Models a) Full model with stator transients b) Sub-transient model c) c) Two-axis model d) One-axis model e) Classical model (const. E behind )

All of these reduced-order models are valid for “long times” except the classical model. The classical model is valid only for a brief period of time – i. e. 0. 2 seconds. This makes it acceptable for “first-swing” stability studies, but not much more. The classical model will not give the correct steady-state solution for a “changed case”.

Damping torques 1. Friction and windage 2. Stator currents (load) 3. Field current (excitation) 4. Damper windings

Look for an integral manifold:

Substitute this into the torque equation. If the time constant is zero (zero-order integral manifold), you get the torque equation of the one-axis model. Since we are keeping the next term (first-order integral manifold), there is an additional torque term:

This can be approximated by a “constant D” damping torque term: That is: using a zero-order integral manifold does not capture any of the effects of the damper winding. However, a firstorder integral manifold does capture some of the damper winding effects.