ECE 501 Introduction to BME ECE 501 Dr
ECE 501 Introduction to BME ECE 501 Dr. Hang

Part V Biomedical Signal Processing Introduction to Wavelet Transform ECE 501 Dr. Hang

Introduction Fourier Analysis ECE 501 Dr. Hang
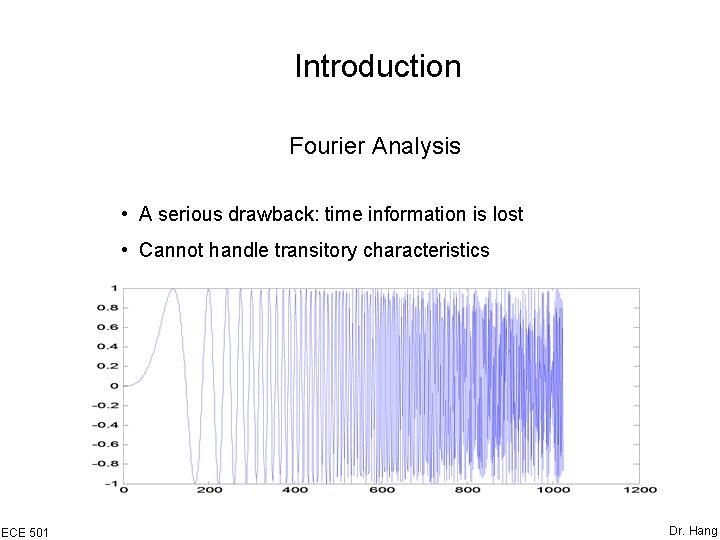
Introduction Fourier Analysis • A serious drawback: time information is lost • Cannot handle transitory characteristics ECE 501 Dr. Hang
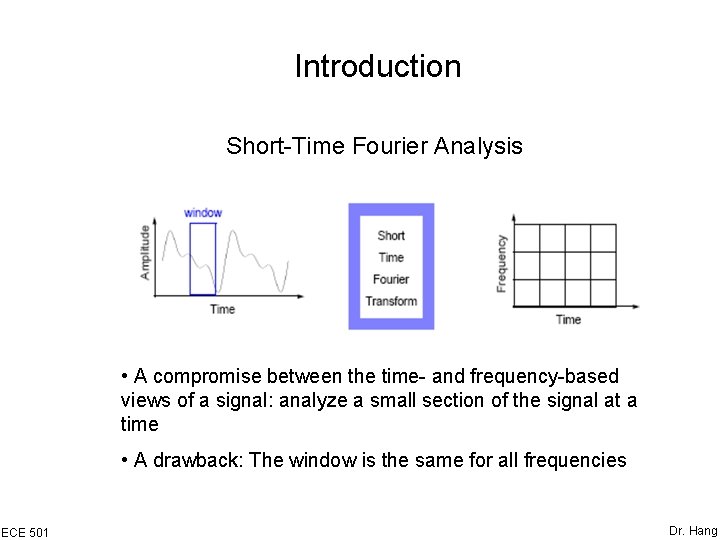
Introduction Short-Time Fourier Analysis • A compromise between the time- and frequency-based views of a signal: analyze a small section of the signal at a time • A drawback: The window is the same for all frequencies ECE 501 Dr. Hang

Introduction Wavelet Analysis • A windowing technique with variable-sized regions: long time interval for low-frequency information, shorter regions for high-frequency information • Time-scale region ECE 501 Dr. Hang
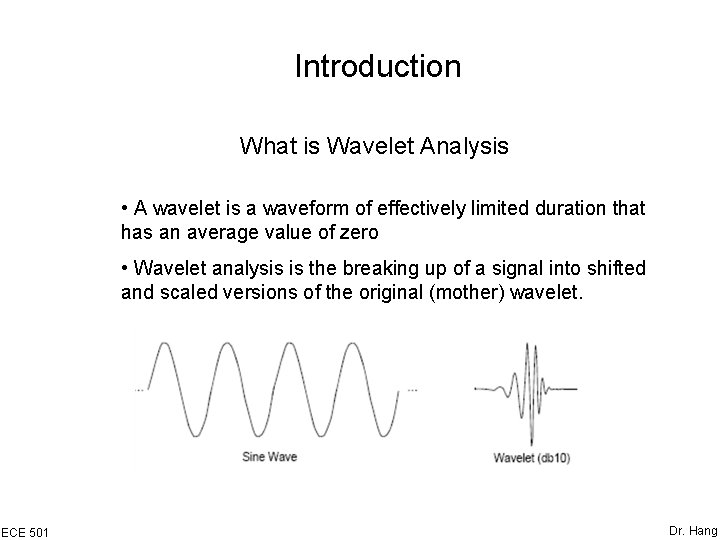
Introduction What is Wavelet Analysis • A wavelet is a waveform of effectively limited duration that has an average value of zero • Wavelet analysis is the breaking up of a signal into shifted and scaled versions of the original (mother) wavelet. ECE 501 Dr. Hang
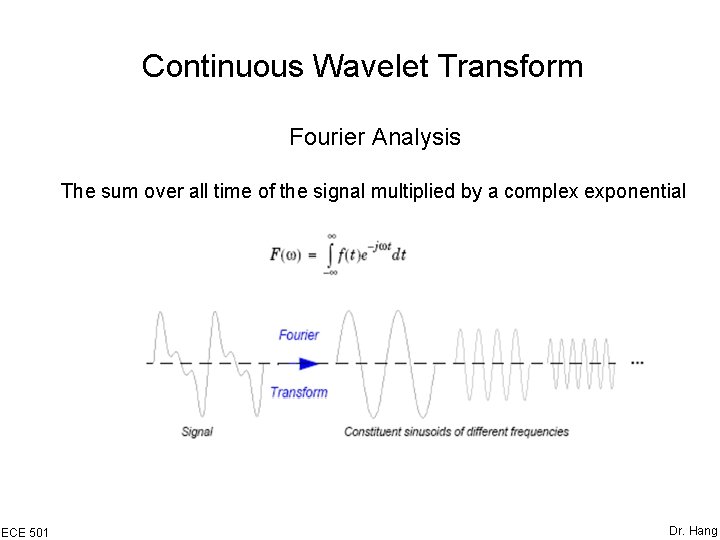
Continuous Wavelet Transform Fourier Analysis The sum over all time of the signal multiplied by a complex exponential ECE 501 Dr. Hang
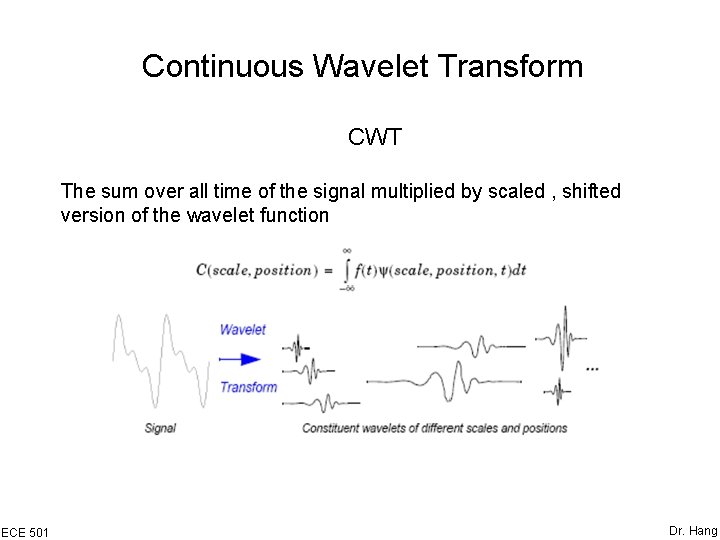
Continuous Wavelet Transform CWT The sum over all time of the signal multiplied by scaled , shifted version of the wavelet function ECE 501 Dr. Hang
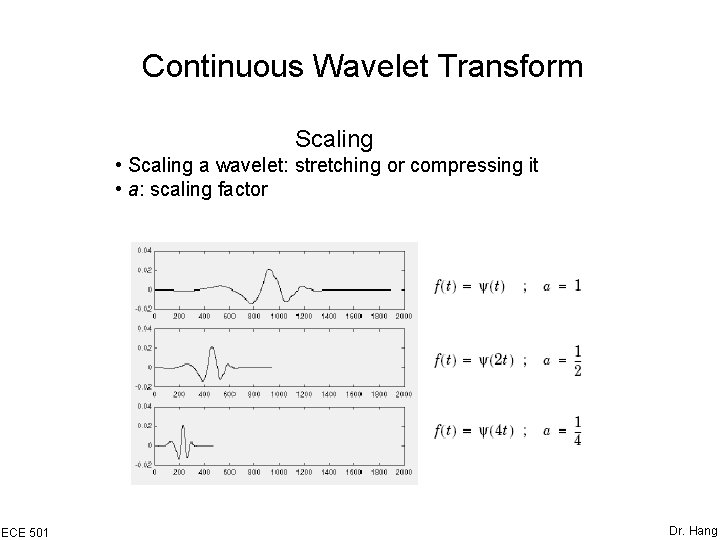
Continuous Wavelet Transform Scaling • Scaling a wavelet: stretching or compressing it • a: scaling factor ECE 501 Dr. Hang
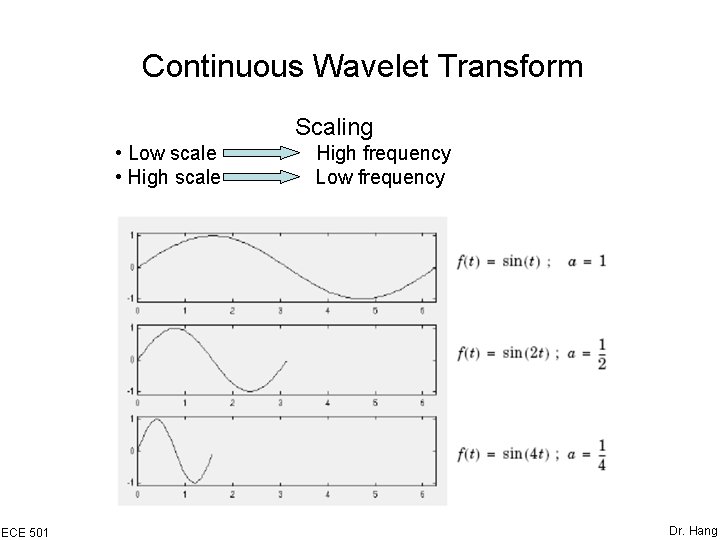
Continuous Wavelet Transform Scaling • Low scale • High scale ECE 501 High frequency Low frequency Dr. Hang
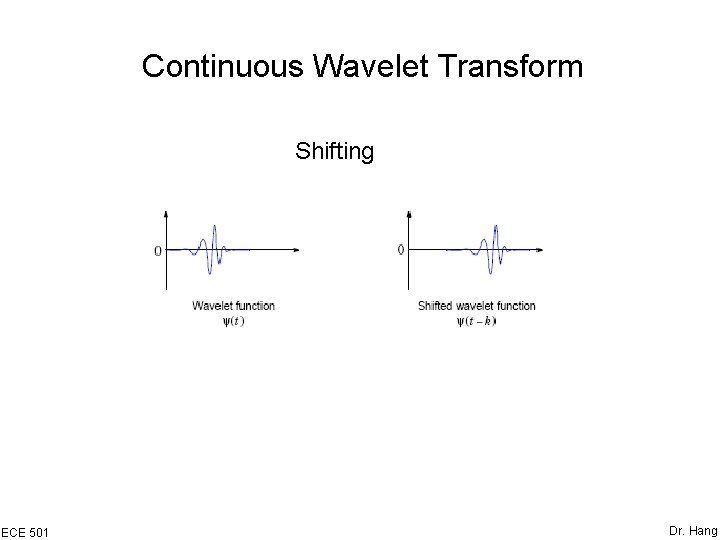
Continuous Wavelet Transform Shifting ECE 501 Dr. Hang

Continuous Wavelet Transform Five Steps to a CWT 1. Take a wavelet and compare it to a section at the start of the original signal 2. Calculate the wavelet coefficient C ECE 501 Dr. Hang

Continuous Wavelet Transform Five Steps to a CWT 3. Shift the wavelet to the right and repeat steps 1 and 2 until the whole signal is covered. ECE 501 Dr. Hang
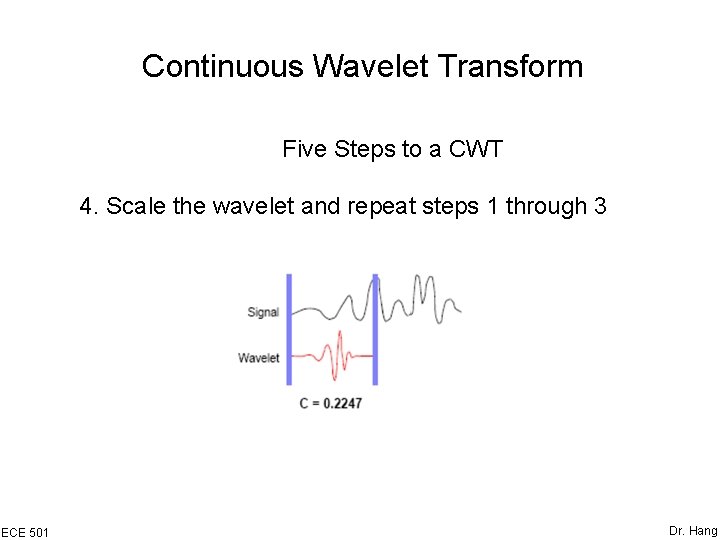
Continuous Wavelet Transform Five Steps to a CWT 4. Scale the wavelet and repeat steps 1 through 3 ECE 501 Dr. Hang

Continuous Wavelet Transform Five Steps to a CWT 5. Repeat steps 1 through 4 for all scales ECE 501 Dr. Hang
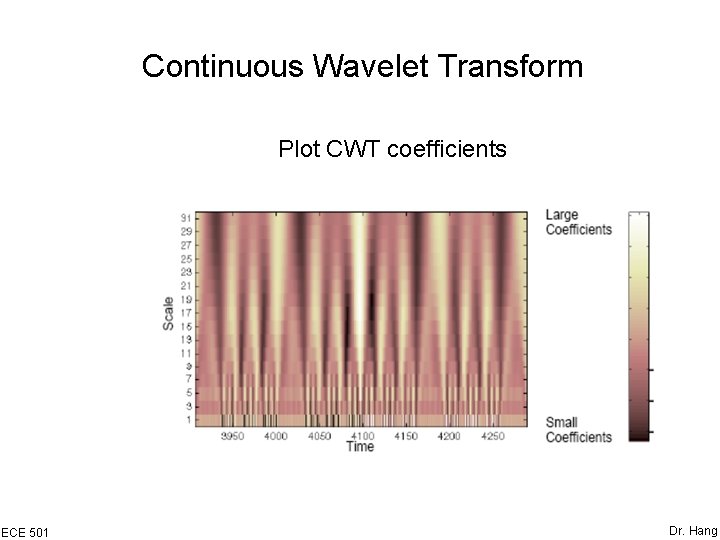
Continuous Wavelet Transform Plot CWT coefficients ECE 501 Dr. Hang
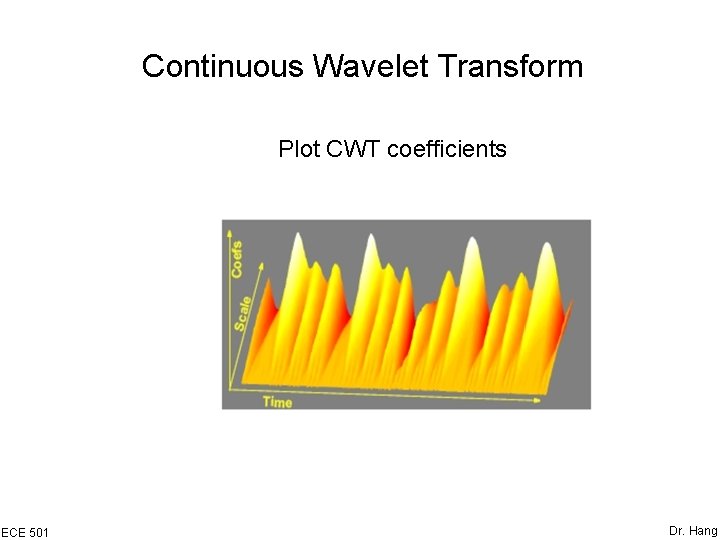
Continuous Wavelet Transform Plot CWT coefficients ECE 501 Dr. Hang

Discrete Wavelet Transform • Dyadic scales and positions: • Mallat algorithm: fast algorithm via filtering • Accurate analysis: compression, denoising ECE 501 Dr. Hang
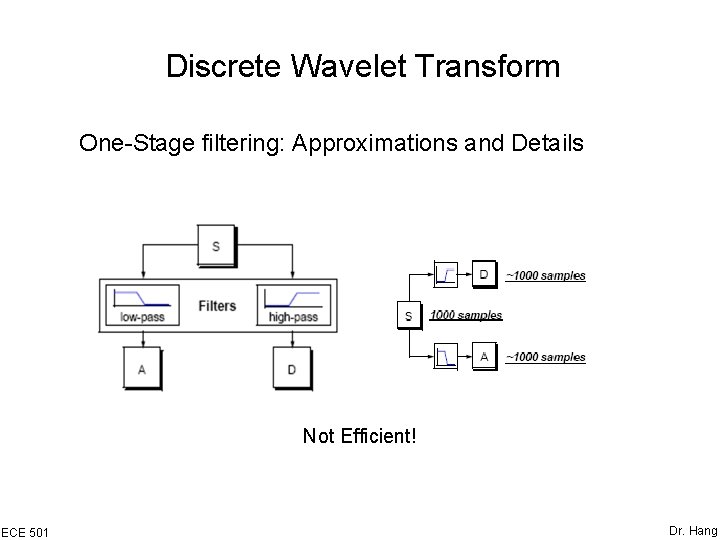
Discrete Wavelet Transform One-Stage filtering: Approximations and Details Not Efficient! ECE 501 Dr. Hang
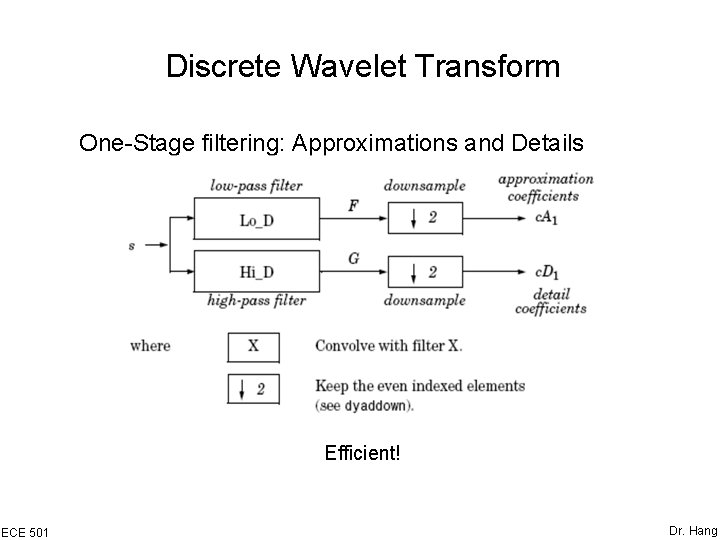
Discrete Wavelet Transform One-Stage filtering: Approximations and Details Efficient! ECE 501 Dr. Hang
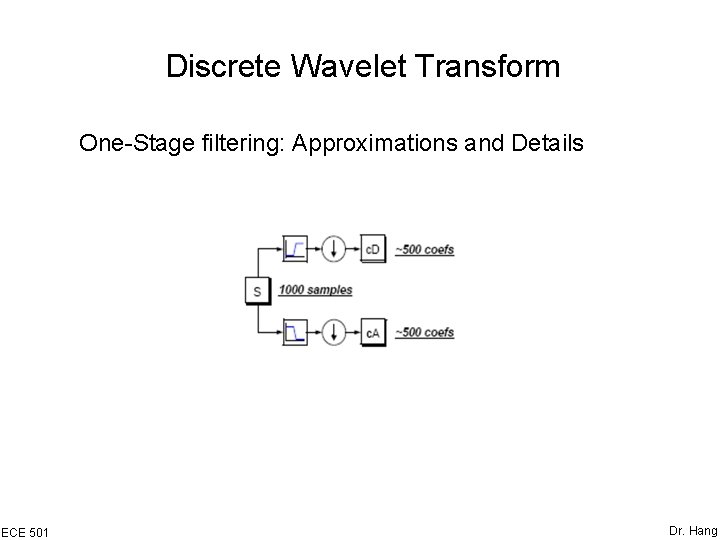
Discrete Wavelet Transform One-Stage filtering: Approximations and Details ECE 501 Dr. Hang
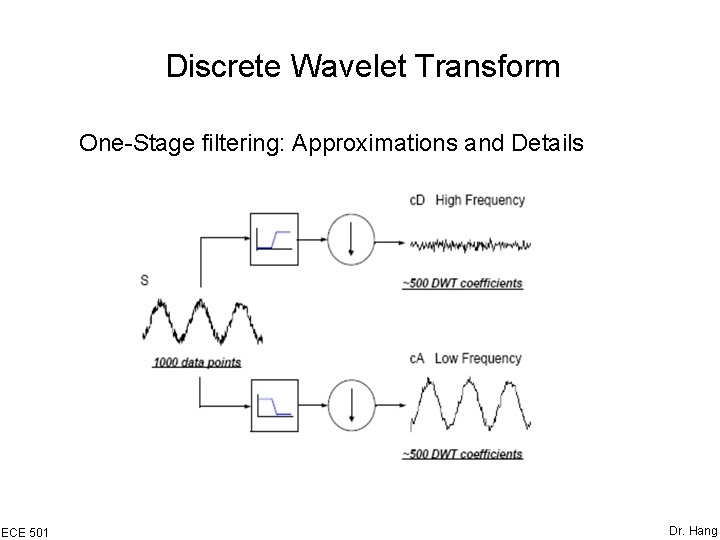
Discrete Wavelet Transform One-Stage filtering: Approximations and Details ECE 501 Dr. Hang
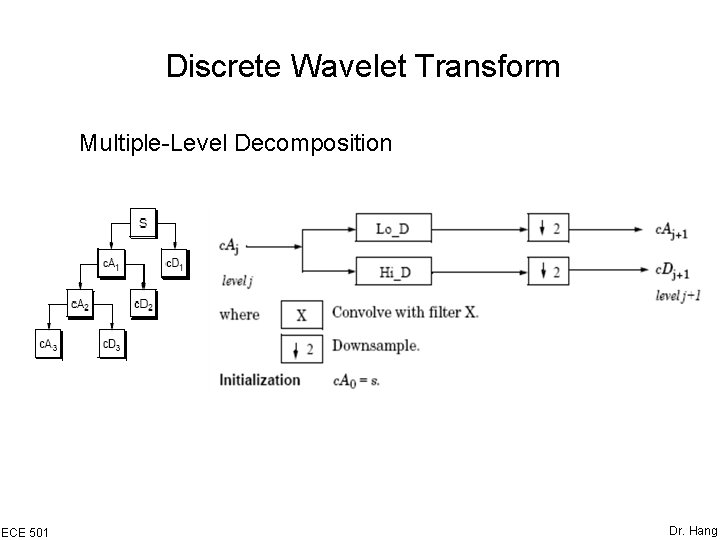
Discrete Wavelet Transform Multiple-Level Decomposition ECE 501 Dr. Hang
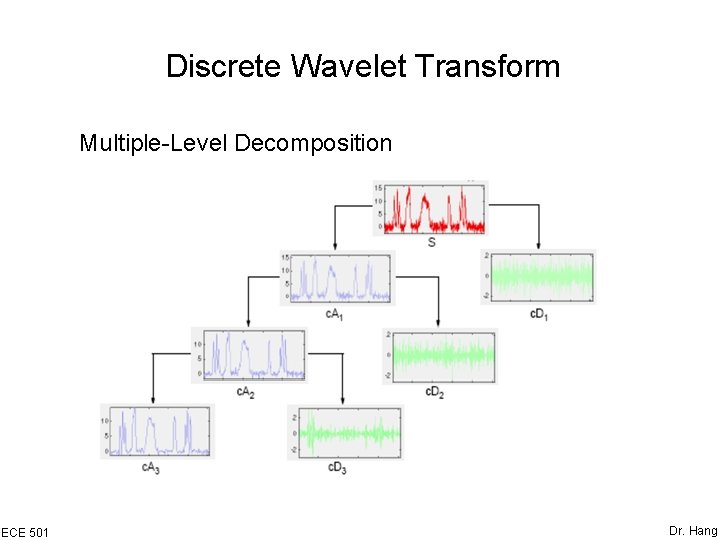
Discrete Wavelet Transform Multiple-Level Decomposition ECE 501 Dr. Hang
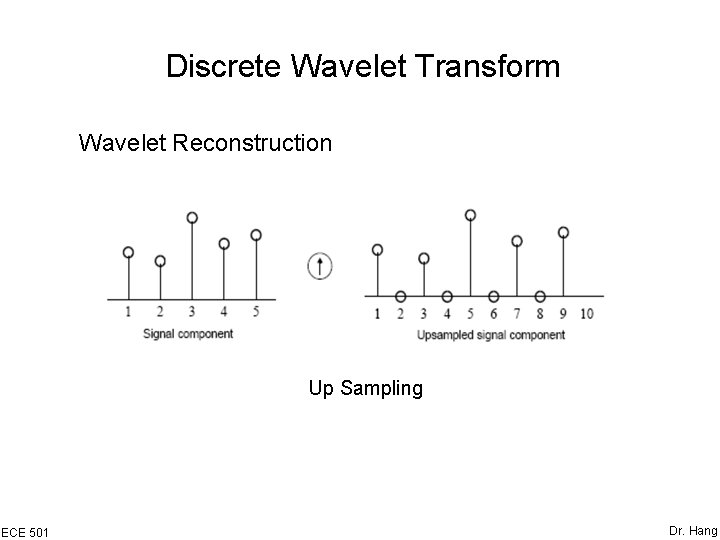
Discrete Wavelet Transform Wavelet Reconstruction Up Sampling ECE 501 Dr. Hang
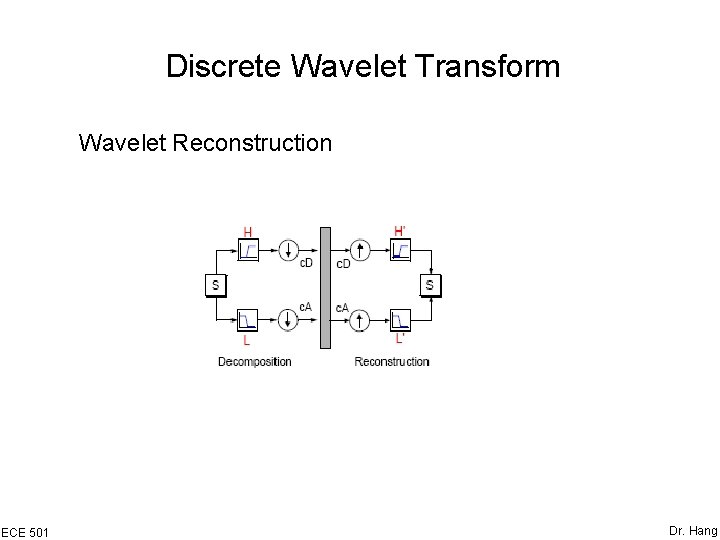
Discrete Wavelet Transform Wavelet Reconstruction ECE 501 Dr. Hang
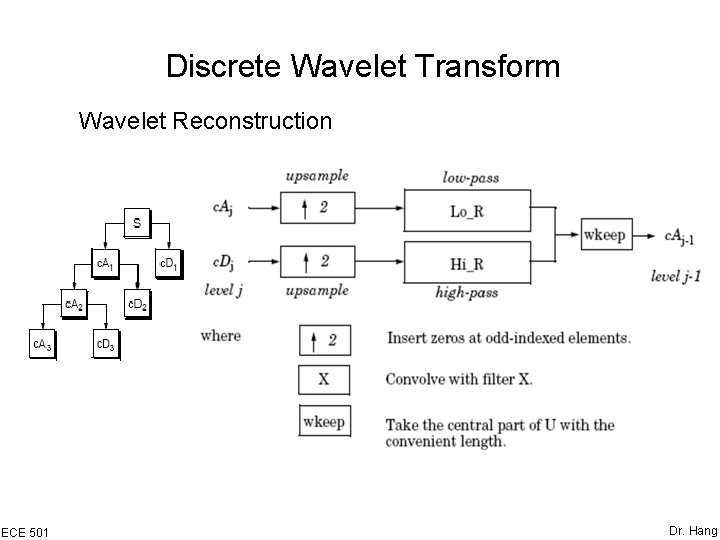
Discrete Wavelet Transform Wavelet Reconstruction ECE 501 Dr. Hang
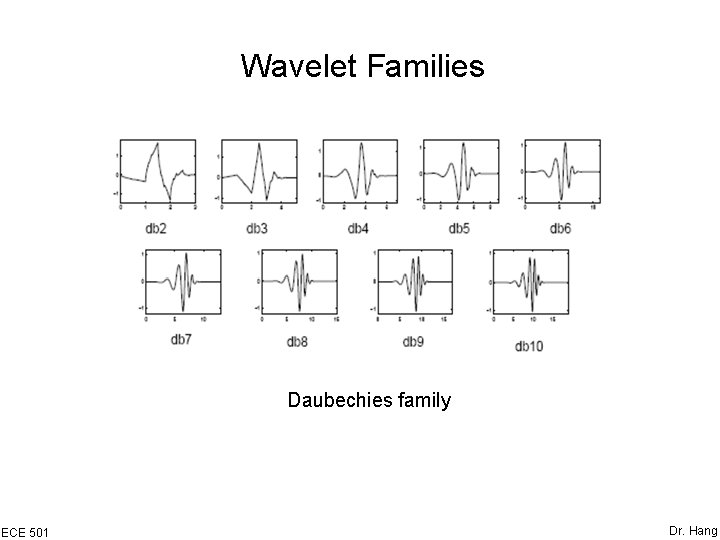
Wavelet Families Daubechies family ECE 501 Dr. Hang
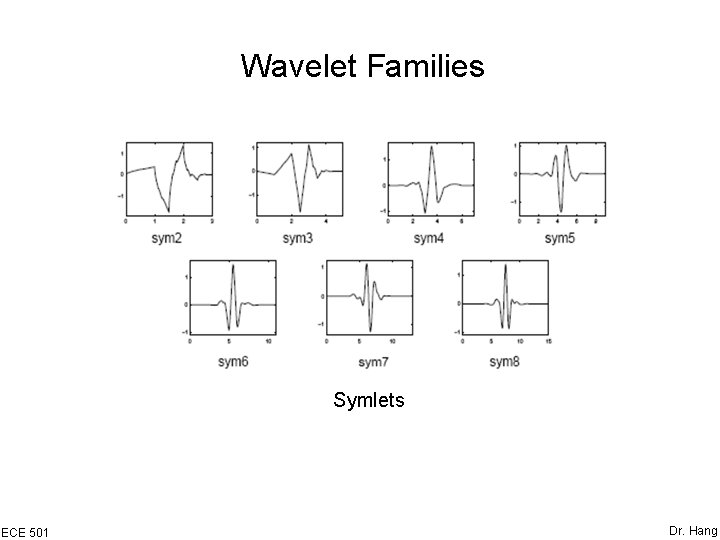
Wavelet Families Symlets ECE 501 Dr. Hang

Denoising 1. Decompose 2. Threshold detail coefficients 3. Reconstruct ECE 501 Dr. Hang
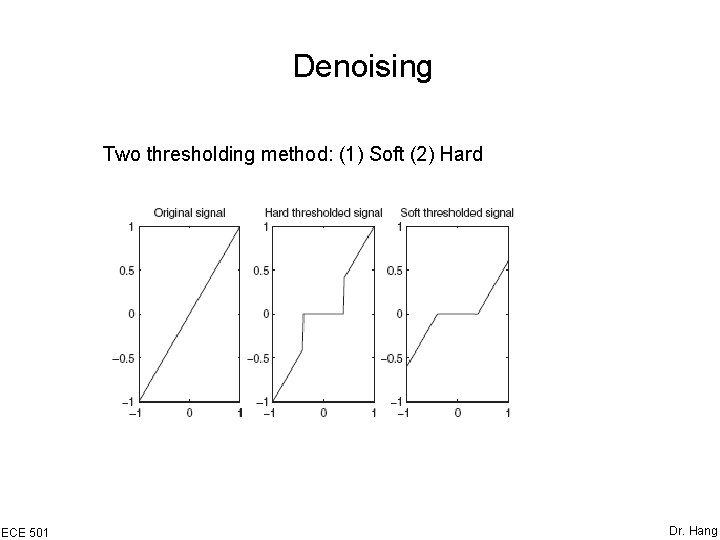
Denoising Two thresholding method: (1) Soft (2) Hard ECE 501 Dr. Hang
- Slides: 32