ECE 497 NC Unconventional Computer Architecture Nicholas Carter

ECE 497 NC: Unconventional Computer Architecture Nicholas Carter Lecture 12: Quantum Computers II – Implementation Issues

Outline • Hurdles to building quantum computers – Decoherence – Error Correction • Requirements for workable quantum computers • NMR quantum computers • Complete architecture proposal

Decoherence • Quantum computations rely on being able to operate on a set of qubits in an entangled/superimposed state – Allows computation on all possible inputs to a computation in parallel • Problem: Interaction of qubits with environment affects their state, causing them to not be entangled/superimposed – Can partially address this by designing computer to reduce interaction with environment, but this may make it impractical (for example, running at very low temperatures) • General result: a quantum computation can only proceed for a limited period of time before a measurement must be performed – Measurement forces the system into a more-stable classical state – Measurement destroys superposition – System limited by ratio of decoherence time to operation latency

Quantum Errors • Digital systems provide noise protection by mapping an analog signal onto two discrete states – Any error/noise that doesn’t cause the system to mis-interpret a signal gets corrected by the next circuit that reads the signal • Problem: qubits are analog – Need to be able to operate on qubits that are superpositions of multiple states – Observation of qubits collapses them into one state or another – Also, operations on qubits are unlikely to be perfect, another source of error • Need error correction

Classic Error Correction • Basic idea: encode n bits of data as n + m bits of errordetecting data. – For codes where the original n bits remain unchanged, the m bits are called the syndrome. – Example: Hamming codes – Well-understood trade-off between m and number of errors that can be corrected/detected • Whenever data is read, regenerate the m syndrome bits – Compare to syndrome from data to determine if error has occurred – Depending on the code, may be able to correct errors as well as just detect

Quantum Error Correction • Problem: reading qubits in a superimposed state collapses them to one state or the other. – Can’t use coding algorithms that require examining the data bits to detect errors • Solution: use codes based on measurements that only determine information about errors, not about data – – Theoretical best code uses 5 qubits to encode 1 Commonly-used code uses 7 qubits for each data qubit. Can recursively apply encoding technique to tolerate higher error probabilities For some codes, can build gates that operate on encoded data directly, without decoding • Code used in paper requires “about 153” physical gates to implement a fault-tolerant operation • Implementation parameter: error rate of technology determines how much logic can be done between error corrections, and thus overhead of error correction.

Requirements for Quantum Computer • Need to have something to represent qubits – Lots of physical phenomena that have two states • Must be able to address individual qubits, and qubits must be able to interact – Must be able to apply individual qubits as inputs to gates – Need to have gates with >1 input • Must be able to initialize qubits to a known state – Hard to write programs if you can’t set inputs • Must be able to observe/extract result from system – Yep, the answer’s in there somewhere, just can’t get it out • Coherence time must be long compared to gate delay – This basically determines how many operations we can do on a superposition before we have to do an observation – Implementation detail visible to programmer

NMR-Based Quantum Computers • • Most advanced demonstrated technology for quantum computation Use nuclei with spin ½ as qubits – – Spin straight up = |0> Spin straight down = |1> Other directions indicate superpositions of |0> and |1> Long coherence times (seconds) • Electron spins (alternate technology) have coherence times of nanoseconds – In a magnetic field, spin direction precesses about the field’s axis at a rate that is proportional to the field strength

NMR-Based Computers II • Bond atoms that represent qubits into molecules – Inter-atomic bonds provide mechanism for different qubits to interact. – Each molecule becomes an n-qubit computing system • Can operate on multiple molecules in parallel to reduce errors – Asymmetry of molecule causes different atoms to precess at different frequencies • Individual addressability

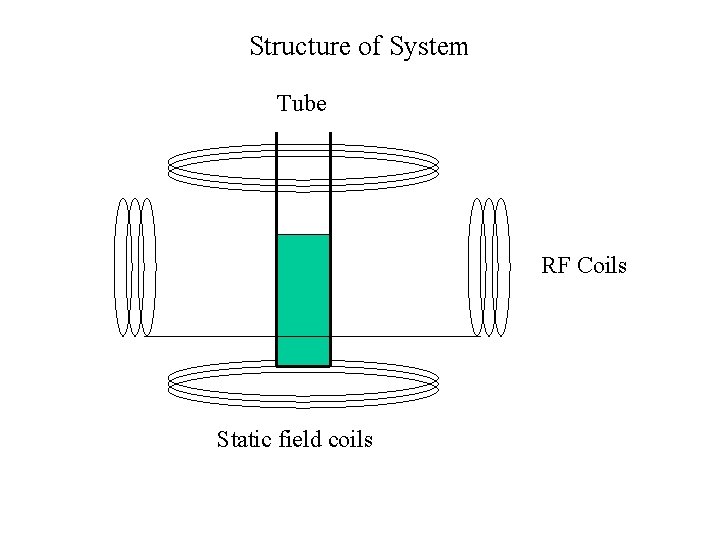
Structure of System Tube RF Coils Static field coils

Implementing Operations • Key ideas: – Radio energy applied perpendicular to magnetic field causes spins to rotate around axis of RF field if RF frequency is a resonant frequency of the precession frequency • Pulses of different durations cause different amounts of rotation – Position of spin of atom A affects precession rate of nearby atom B by altering the magnetic field seen by B – Differences between precession frequencies of different atoms in the molecule >> effect of nearby atom spins

Implementing Operations I • Can flip state of bit with appropriately-timed RF pulse, or set into superposition with shorter pulse • Can create multi-input gates by sending pulses at the frequency that the atom will precess at if appropriate other bits are in a given state. – CNOT operation • CNOT operation + set of operations on individual qubits = universal set of gates • “Machine language” is now set of frequency of RF pulses, duration of pulses, and time between pulses • Read state out by rotating qubit spins into horizontal plane, sensing the time-varying magnetic field they create as they precess

Results • Used NMR technology to implement the core of Shor’s algorithm on permutations of a four-element set. • Duration: 50 -500 ms, depending on permutation

Full System Architecture • Goal: extend thoughts on ways to do computation with quantum to something like a full system • Issues – Data storage – Communication/signalling – Error correction overhead • Basic idea: Couple quantum computing system with classical computer – Classical computer sequences operations through quantum computer, does dynamic compilation – Classical computer also does checking of results for probabilistic computations • System aimed at NP-complete problems where computing answer is hard but checking answer is easy.

Programming/Compiling • Two-phase process • Pre-compiler generates code that executes the algorithm with a specified error probability on an ideal quantum computer • Dynamic compiler creates instruction stream to meet the error probability on the actual computer – This compiler needs to know about the technology – Also needs estimate of program run time • #errors is proportional to run time. • Estimate either provided by user or generated using profiling – For example, can start with very conservative (strong) error correction and use lower levels once the running time is known

Error Correction • Problem: 7 -bit codes only tolerate certain amounts of error – Can tolerate greater errors by recursive coding, at greatly increased cost – “Sawtooth” overhead as error rates cross critical thresholds • Solution: Cluster operations – Rather than performing error correction on each operation, group operations into clusters and only do error correction after each cluster. – Allows “fractional” levels of recursion, bringing error correction cost much closer to ideal.

Architecture • Quantum ALU/Ancilla generator – Performs actual computations and error correction – Implements set of universal quantum operations • Quantum Memories – Storage locations for qubits – Assumed to have 2 orders of magnitude lower error rates than CPU • Entropy Exchange Unit – Source of qubits in |0> or CAT state – Important, because many algorithms require many qubits in one of these states or the other • Inter-unit communication via quantum teleportation – Allows exact state of qubits to be transmitted – Extension to quantum teleportation allows conversion from one error-correcting code to another as part of teleportation

Conclusions/Thoughts • Quantum computing is still way out there, though people are starting to demonstrate actual systems • One issue: current designs expose implementation issues to programmer – Time that computation can run before decoherence becomes an issue – Number of steps that can be performed before need to do a measurement • Still big gaps between demonstrated results and theoretical predictions people are using to do designs • My gut feelings: – We’ll see quantum computers being built for specific problems in the next decade or two – Quantum computing won’t move into the mainstream unless a vastly better implementation technology is developed and a much larger set of problems that are good for quantum are discovered