ECE 383ME 442 Intro to Robotics and Automation

ECE 383/ME 442: Intro to Robotics and Automation Linear Algebra for 3 D Transformations

Agenda • Readings • Principles, 3. 5 -6 • Planning Algorithms, Ch. 3. 2 • Rigid transformations

Rigid Objects

Biological systems, virtual characters

Articulated Robot q 2 q 1 • Robot: usually a rigid articulated structure • Geometric CAD models, relative to movable reference frames • A configuration specifies the placement of those frames

Rigid Transformations • At the heart of robotics… • For planning and control • Collision avoidance • Deciding how to move in joint space to produce desired motion in workspace • For modeling physics • Effects of gravity on joints • Understanding how contact forces affect joint torques • Convert data gathered in one coordinate frame to another… • From distance readings to absolute positions • An “eye-in-hand” camera • Two 3 D scans from two different poses

Coordinates, Points and Displacements • A point X in space can be represented for the purposes of calculations (not in the realm of pure thought) as a set of coordinates in a privileged reference frame TW, called the world frame. • The representation of a point P is an array of numbers, called its coordinates • The coordinates change depending on the choice of FW • When comparing or manipulating two points, their representations as vectors must use the reference frames! • The coordinates of a displacement (or direction) from point X to Y are the same regardless of the world frame origin • But they change depending on its orientation • Only the following operations make sense (in a common frame) : • P-P=D, P+D=P, D+D=D

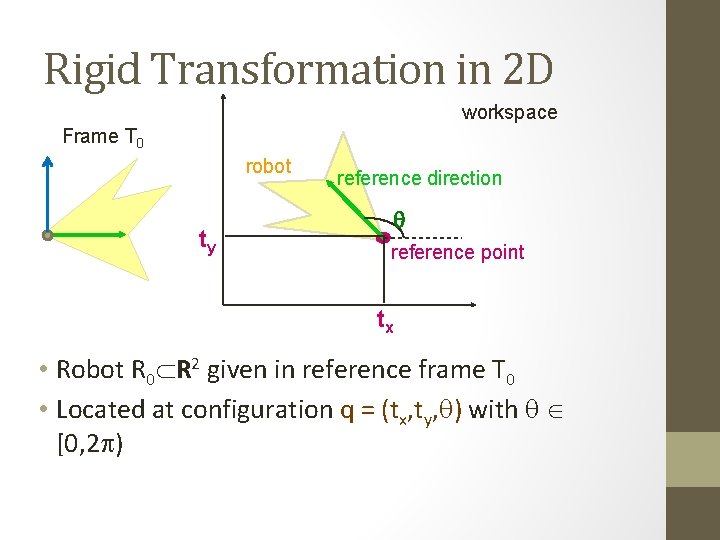
Rigid Transformation in 2 D workspace Frame T 0 robot ty reference direction q reference point tx • Robot R 0 R 2 given in reference frame T 0 • Located at configuration q = (tx, ty, q) with q [0, 2 p)

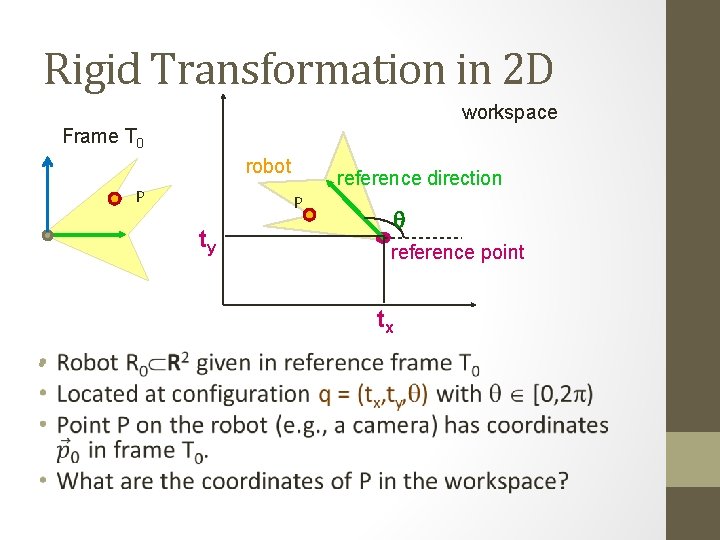
Rigid Transformation in 2 D workspace Frame T 0 robot P reference direction P ty q reference point tx •

Rigid Transformation in 2 D •

Rotations in 2 D -sin q • cos q q cos q sin q

Rotations in 2 D -sin q • cos q q px py cos q sin q

Rotations in 2 D -sin q • cos q q cos q sin q pxcos q -pysin q px py pxsin q + pycos q

Dot product •

Properties of the dot product •

Matrix-vector multiplication •

General equations •

Multiple rotations •

Matrix-matrix multiplication •

Rotation matrix-matrix multiplication •

General definition •

Other Fun Facts •

Consequence: rotation inverse •

Break

Rigid Transformation in 2 D • q = (tx, ty, q) with q [0, 2 p) • Robot R 0 R 2 given in reference frame T 0 • What’s the new robot Rq? {Tq(x, y) | (x, y) R 0} • Define rigid transformation Tq(x, y) : R 2 Tq(x, y) = cos θ -sin θ cos θ 2 D rotation matrix x y + tx ty Affine translation

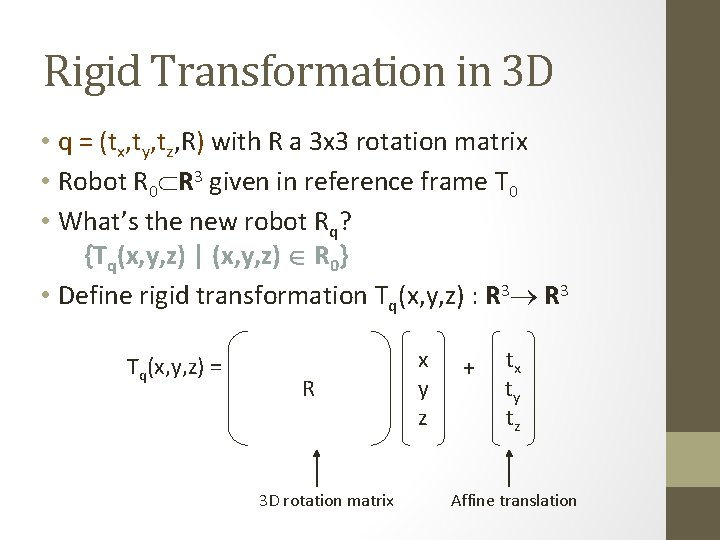
Rigid Transformation in 3 D • q = (tx, ty, tz, R) with R a 3 x 3 rotation matrix • Robot R 0 R 3 given in reference frame T 0 • What’s the new robot Rq? {Tq(x, y, z) | (x, y, z) R 0} • Define rigid transformation Tq(x, y, z) : R 3 Tq(x, y, z) = R 3 D rotation matrix x y z + tx ty tz Affine translation

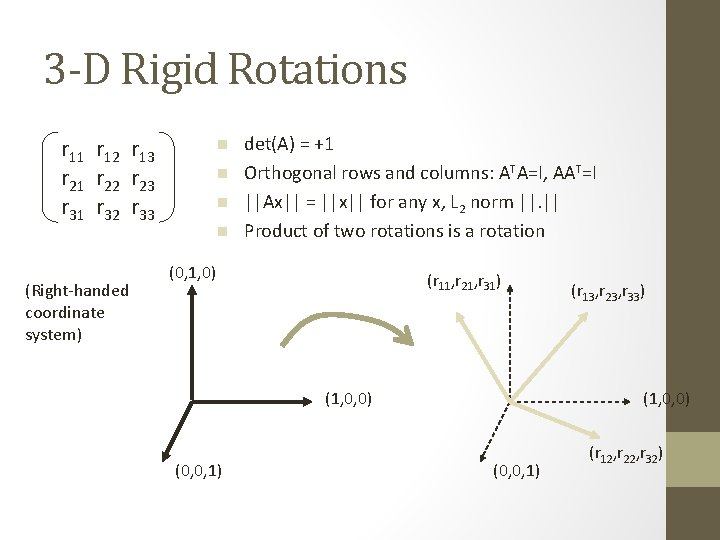
3 -D Rigid Rotations r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 (Right-handed coordinate system) n n det(A) = +1 Orthogonal rows and columns: ATA=I, AAT=I ||Ax|| = ||x|| for any x, L 2 norm ||. || Product of two rotations is a rotation (0, 1, 0) (r 11, r 21, r 31) (1, 0, 0) (0, 0, 1) (r 13, r 23, r 33) (1, 0, 0) (0, 0, 1) (r 12, r 22, r 32)

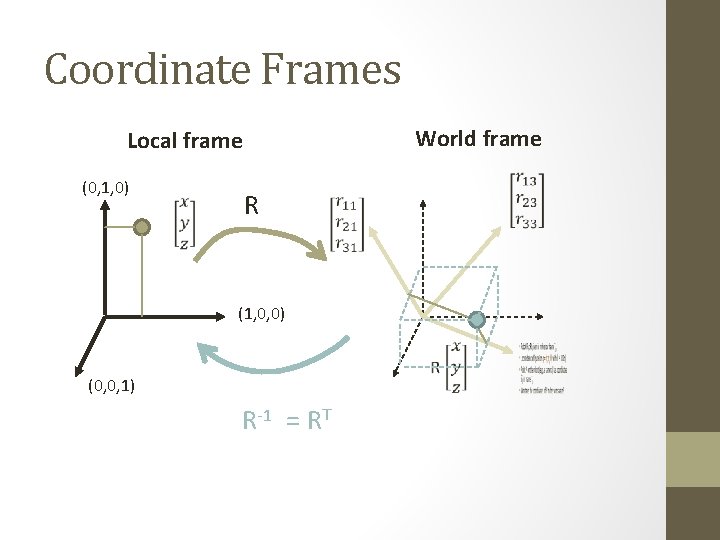
Coordinate Frames World frame Local frame (0, 1, 0) R (1, 0, 0) (0, 0, 1) R-1 = RT

Transformation inverse •

Note: transforming points vs directional quantities • Rigid transform q = (tx, ty, q) • A point with coordinates (x, y) in T 0 undergoes rotation and affine translation Tq(x, y) = cos θ -sin θ cos θ x y + tx ty • Directional quantities (e. g. , velocity, force) are not affected by the affine translation! Rq(vx, vy) = cos θ -sin θ cos θ vx vy

Transform Hell

Becoming a master of transformations… • Rule #1: Comparisons between vectors only makes sense if their coordinates are in the same reference frame! • When many vectors / matrices are floating around, keeping track can get very confusing • Tip: use subscripts to denote frame • Rule #2: Converting vectors to a different reference frame require applying a transformation • You need to know the transformation between reference frames • Rule #3: Mind your P’s and D’s • P-P=D, P+D=P, D+D=D, D*c=D • Do not do P+P, P*c! • D’s don’t “feel” translation • Rule #4: if you know the transformation from every frame to the world frame, you can transform between any two frames

Homogeneous coordinates • Sorting out positions from directions is somewhat messy, is there a better way? • Homogeneous coordinates: • Add a 3 rd component, w • w=1 indicates a point, w=0 indicates a direction • In normal coordinates, [x, y, w]T represents a point [x/w, y/w]T • Directions are “points at infinity”

Homogeneous transforms •

Homogeneous transforms in 3 D •

Does this solve all our transform confusion? • No, it still doesn’t enforce consistency of reference frames, or prohibit operations like P+P or P*c.

Next Time • 3 D rotations • Readings: • Principles, Appendix E