ECE 331 Digital System Design Minimizing Boolean Expressions

ECE 331 – Digital System Design Minimizing Boolean Expressions using K-maps, The Minimal Cover, and Incompletely Specified Boolean Functions (Lecture #6)

Minimizing SOP Expressions ECE 331 - Digital System Design 2

Remember … 1. A Canonical SOP expression can be derived from a Truth table. 2. A shorthand notation can be used to describe a SOP expression. ECE 331 - Digital System Design 3
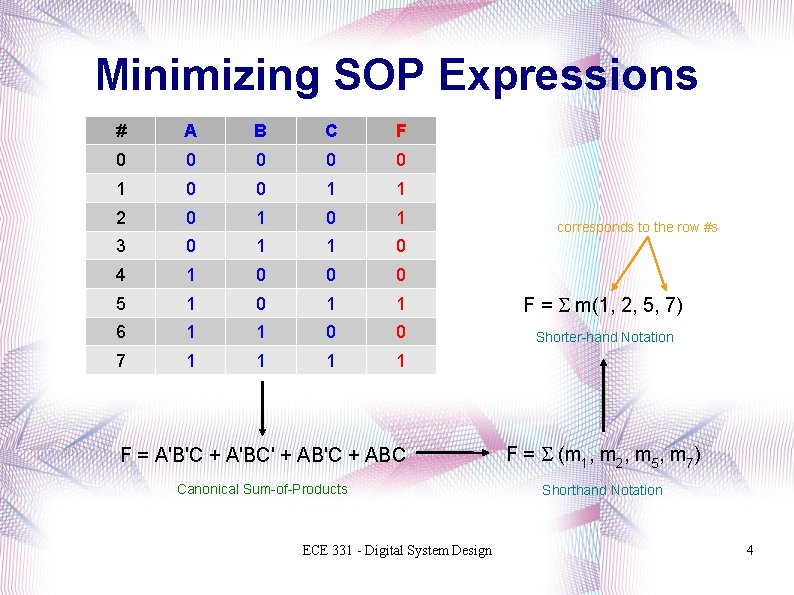
Minimizing SOP Expressions # A B C F 0 0 0 1 1 2 0 1 3 0 1 1 0 4 1 0 0 0 5 1 0 1 1 F = S m(1, 2, 5, 7) 6 1 1 0 0 Shorter-hand Notation 7 1 1 corresponds to the row #s F = A'B'C + A'BC' + AB'C + ABC F = S (m 1, m 2, m 5, m 7) Canonical Sum-of-Products Shorthand Notation ECE 331 - Digital System Design 4

Minimizing SOP Expressions Exercise: Given the following Canonical SOP expression: F(A, B, C) = S m(1, 2, 5, 7) 1. Write out the expression in terms of the minterms. 2. Minimize the SOP expression using a K-Map ECE 331 - Digital System Design 5

Minimizing SOP Expressions Exercise: Given the following Canonical SOP expression: F(A, B, C) = S m(0, 2, 3, 6) 1. Write out the expression in terms of the minterms. 2. Minimize the SOP expression using a K-Map ECE 331 - Digital System Design 6

Minimizing SOP Expressions Exercise: Given the following Canonical SOP expression: F(A, B, C, D) = S m(0, 4, 8, 10, 11, 12, 13, 15) 1. Write out the expression in terms of the minterms. 2. Minimize the SOP expression using a K-Map ECE 331 - Digital System Design 7

Minimizing POS Expressions ECE 331 - Digital System Design 8
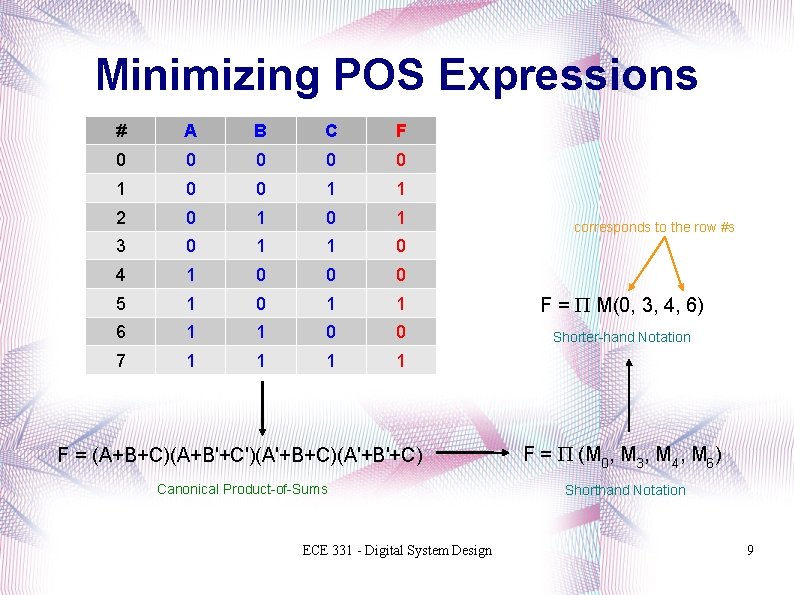
Minimizing POS Expressions # A B C F 0 0 0 1 1 2 0 1 3 0 1 1 0 4 1 0 0 0 5 1 0 1 1 F = P M(0, 3, 4, 6) 6 1 1 0 0 Shorter-hand Notation 7 1 1 corresponds to the row #s F = (A+B+C)(A+B'+C')(A'+B+C)(A'+B'+C) F = P (M 0, M 3, M 4, M 6) Canonical Product-of-Sums Shorthand Notation ECE 331 - Digital System Design 9

Minimizing POS Expressions Exercise: Given the following Canonical POS expression: F(A, B, C) = P M(4, 5, 6) 1. Write out the expression in terms of the minterms. 2. Minimize the POS expression using a K-Map ECE 331 - Digital System Design 10

Minimizing POS Expressions Exercise: Given the following Canonical POS expression: F(A, B, C) = P M(1, 2, 3, 5) 1. Write out the expression in terms of the minterms. 2. Minimize the POS expression using a K-Map ECE 331 - Digital System Design 11

Minimizing POS Expressions Exercise: Given the following Canonical POS expression: F(A, B, C, D) = P M(0, 1, 4, 8, 9, 12, 15) 1. Write out the expression in terms of the minterms. 2. Minimize the POS expression using a K-Map ECE 331 - Digital System Design 12

Selecting a Minimal Cover ECE 331 - Digital System Design 13

Definitions Literal: each appearance of a variable, either uncomplemented or complemented Implicant: a product term that implies F=1 Prime Implicant: an implicant that cannot be combined into another implicant that has fewer literals Cannot be further minimized Essential Prime Implicant: a prime implicant that covers a minterm uniquely. ECE 331 - Digital System Design 14

Definitions F AB 00 01 11 10 0 1 1 1 1 0 C Which are the implicants, prime implicants, and essential prime implicants? ECE 331 - Digital System Design 15

Definition: Implicants F AB 00 01 11 10 0 1 1 1 1 0 C Implicants: A'B'C', A'B'C, A'BC', A'BC, ABC ECE 331 - Digital System Design (minterms) 16
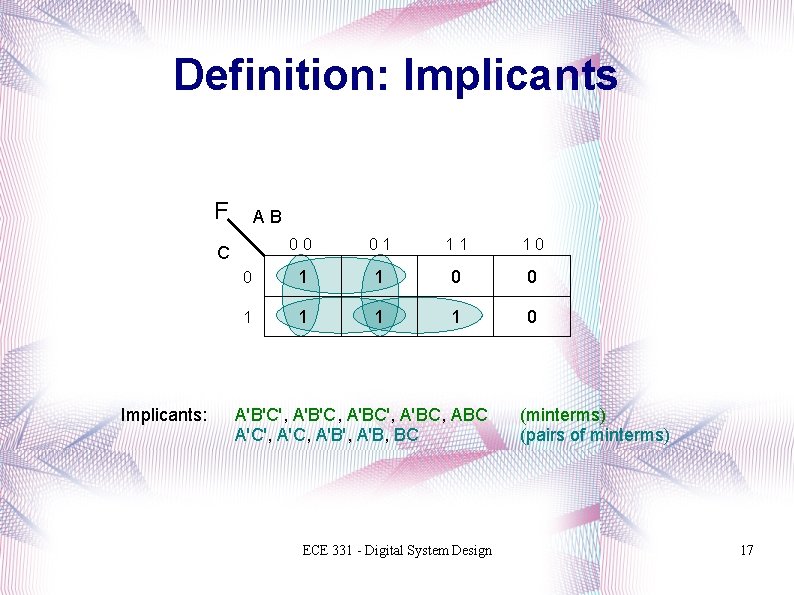
Definition: Implicants F AB 00 01 11 10 0 1 1 1 1 0 C Implicants: A'B'C', A'B'C, A'BC', A'BC, ABC A'C', A'C, A'B', A'B, BC ECE 331 - Digital System Design (minterms) (pairs of minterms) 17
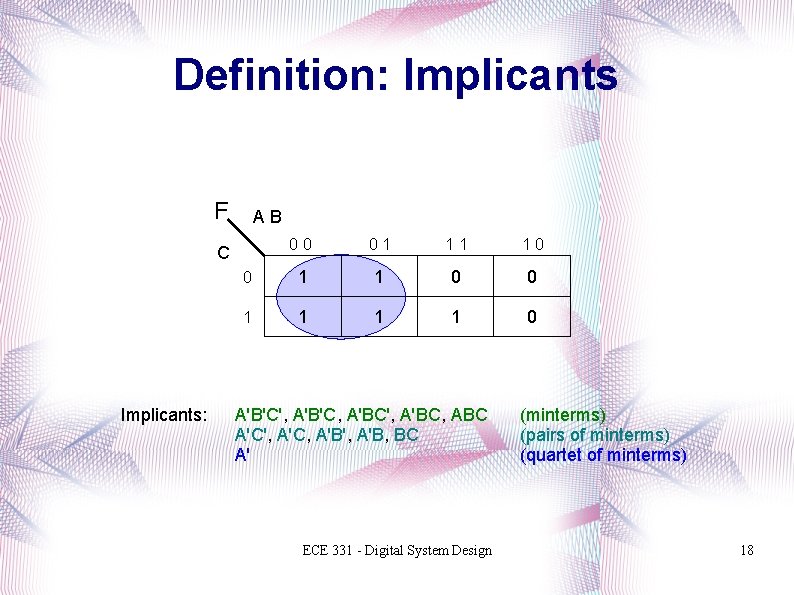
Definition: Implicants F AB 00 01 11 10 0 1 1 1 1 0 C Implicants: A'B'C', A'B'C, A'BC', A'BC, ABC A'C', A'C, A'B', A'B, BC A' ECE 331 - Digital System Design (minterms) (pairs of minterms) (quartet of minterms) 18
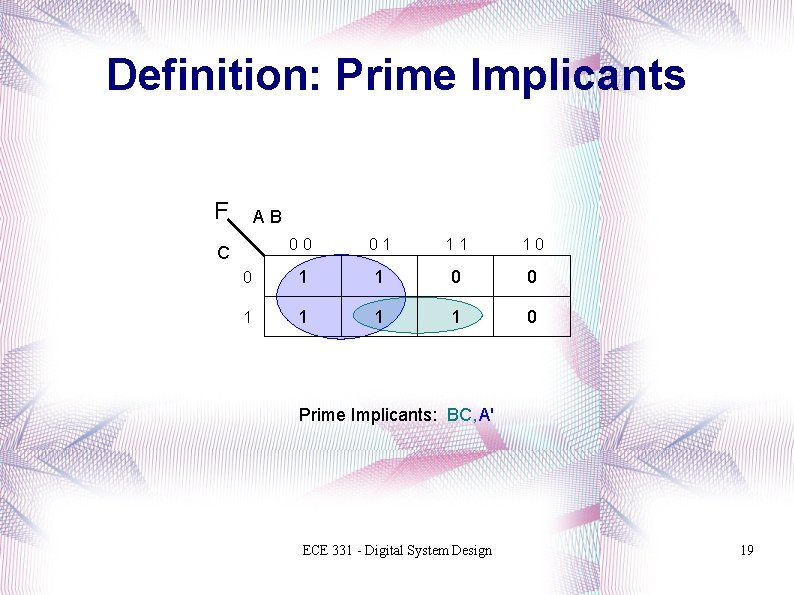
Definition: Prime Implicants F AB 00 01 11 10 0 1 1 1 1 0 C Prime Implicants: BC, A' ECE 331 - Digital System Design 19
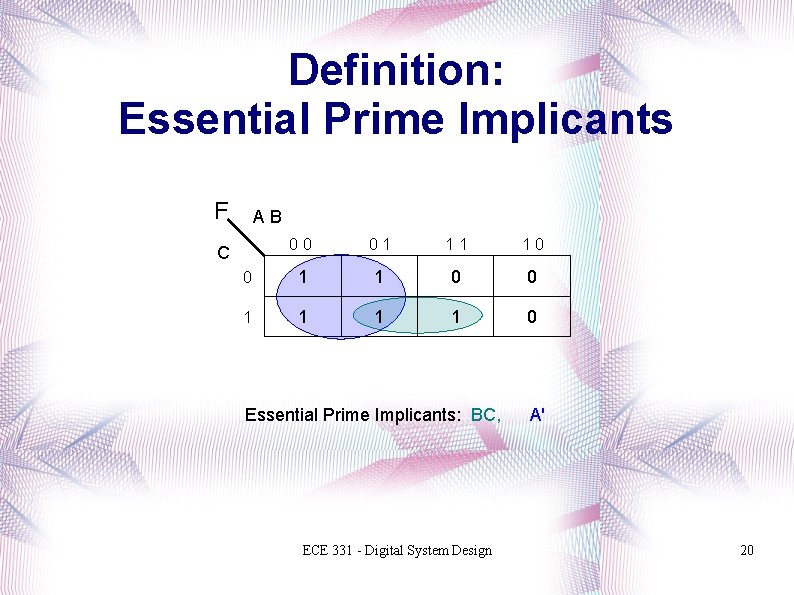
Definition: Essential Prime Implicants F AB 00 01 11 10 0 1 1 1 1 0 C Essential Prime Implicants: BC, ECE 331 - Digital System Design A' 20

Definitions Minimal Cover (SOP): the sum (ORing) of prime implicants Solution may not be unique For SOP, must cover each “ 1” at least once A minimal solution is one with the fewest product terms in the SOP expression, and the fewest literals in each product term. ECE 331 - Digital System Design 21

Selecting a Minimal Cover (SOP) Identify all prime implicants Select all essential prime implicants Select prime implicant(s) to cover remaining terms by considering all possibilities Sometimes selection is obvious Sometimes “guess” next prime implicant Continue, perhaps recursively Try all possible “guesses” Write minimum Boolean expression May not be unique ECE 331 - Digital System Design 22

Selecting a Minimal Cover Example: Determine the minimal cover for the following K-Map: F c d a b 00 01 11 10 00 0 1 1 0 01 1 0 11 1 0 1 1 10 0 0 1 1 1. Identify Prime Implicants 2. Identify Essential Prime Implicants 3. Determine Minimal Cover ECE 331 - Digital System Design 23
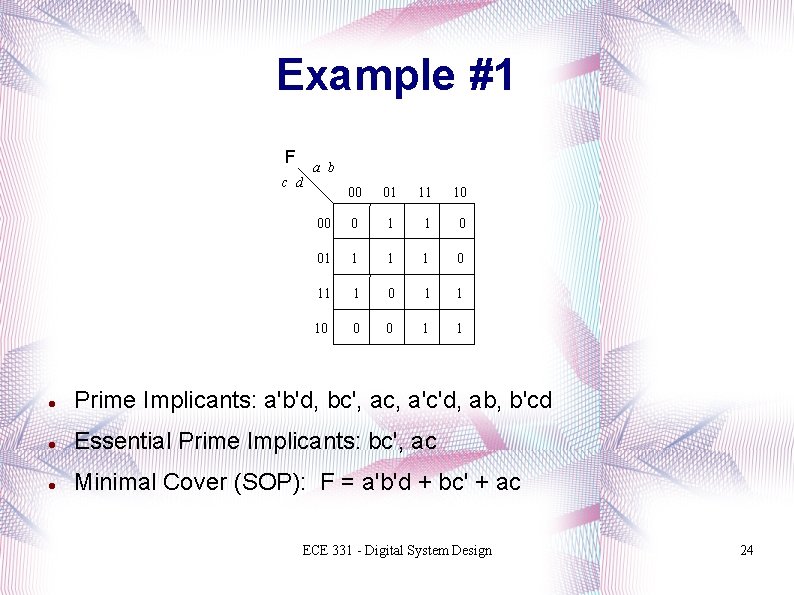
Example #1 F c d a b 00 01 11 10 00 0 1 1 0 01 1 0 11 1 0 1 1 10 0 0 1 1 Prime Implicants: a'b'd, bc', ac, a'c'd, ab, b'cd Essential Prime Implicants: bc', ac Minimal Cover (SOP): F = a'b'd + bc' + ac ECE 331 - Digital System Design 24

Selecting a Minimal Cover Example: Determine the minimal cover for the following K-Map: F w x y z 00 01 11 10 00 0 0 01 1 0 11 1 0 1 1 10 0 0 1. Identify Prime Implicants 2. Identify Essential Prime Implicants 3. Determine Minimal Cover ECE 331 - Digital System Design 25
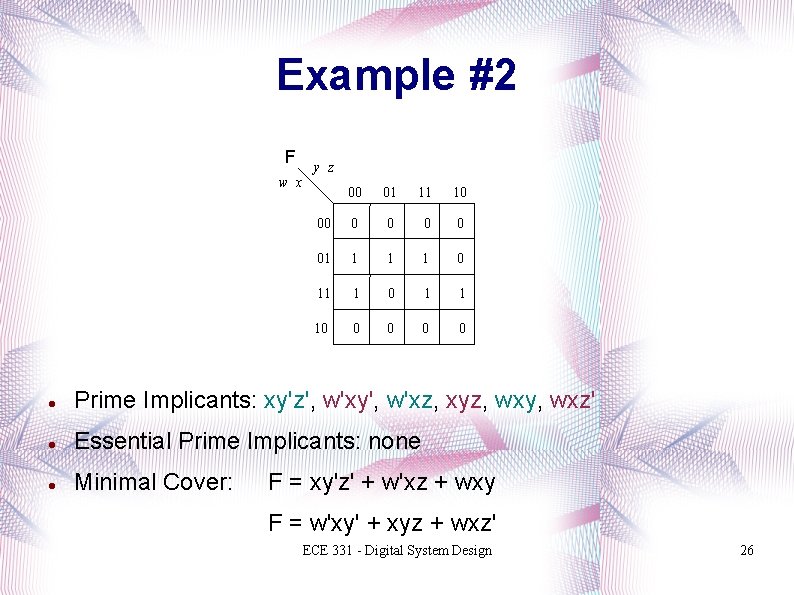
Example #2 F w x y z 00 01 11 10 00 0 0 01 1 0 11 1 0 1 1 10 0 0 Prime Implicants: xy'z', w'xy', w'xz, xyz, wxy, wxz' Essential Prime Implicants: none Minimal Cover: F = xy'z' + w'xz + wxy F = w'xy' + xyz + wxz' ECE 331 - Digital System Design 26

Incompletely Specified Functions ECE 331 - Digital System Design 27

Incompletely Specified Functions Some minterms should (or will) never occur. For example, Binary Coded Decimal (BCD) These are considered “don't care” outputs. When minimizing a SOP expression using a KMap, treat a “don't care” as a “ 1” whenever it is beneficial. When minimizing a POS expression using a KMap, treat a “don't care” as a “ 0” whenever it is beneficial. ECE 331 - Digital System Design 28

Incompletely Specified Functions Exercise: Derive the minimum SOP expression for the following incompletely specified logic function: F(A, B, C, D) = S m(2, 4, 5, 6, 10) + D(12, 13, 14, 15) ECE 331 - Digital System Design 29

Incompletely Specified Functions Exercise: Derive the minimum POS expression for the following incompletely specified logic function: F(A, B, C, D) = S m(2, 4, 5, 6, 10) + D(12, 13, 14, 15) ECE 331 - Digital System Design 30
- Slides: 30