ECE 3163 8443Signals Pattern and Recognition ECE Systems

ECE 3163 8443––Signals Pattern and Recognition ECE Systems LECTURE 33: BODE PLOTS AND FILTERS • Objectives: First-Order System Second-Order System Poles and Zeros Butterworth Filters Chebyshev Filters Frequency Transformations • Resources: MIT 6. 003: Lecture 18 Wiki: Bode Plots EC: Bode Plots Wiki: Butterworth Filters Wiki: Chebyshev Filters URL: Audio:

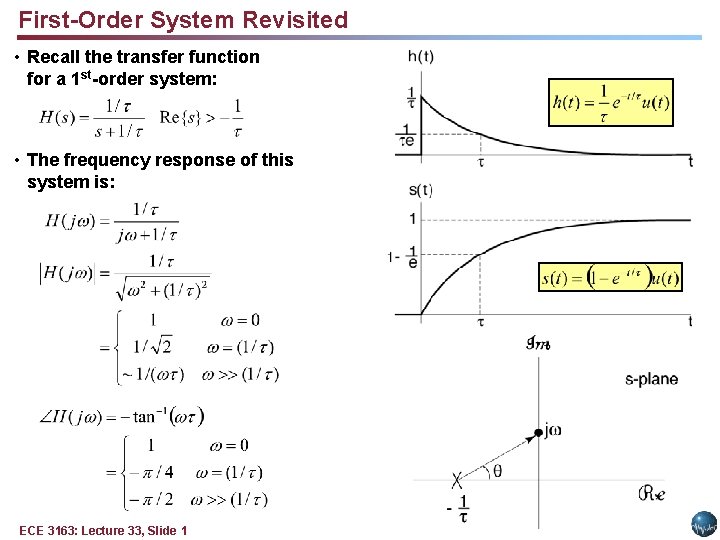
First-Order System Revisited • Recall the transfer function for a 1 st-order system: • The frequency response of this system is: ECE 3163: Lecture 33, Slide 1

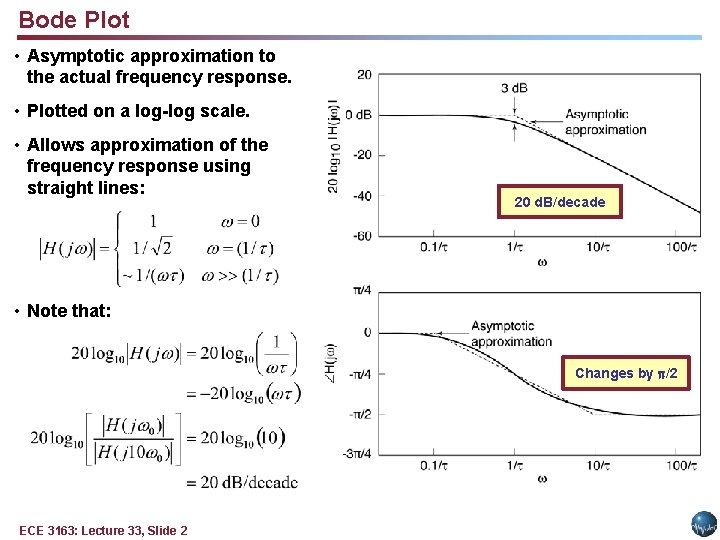
Bode Plot • Asymptotic approximation to the actual frequency response. • Plotted on a log-log scale. • Allows approximation of the frequency response using straight lines: 20 d. B/decade • Note that: Changes by /2 ECE 3163: Lecture 33, Slide 2

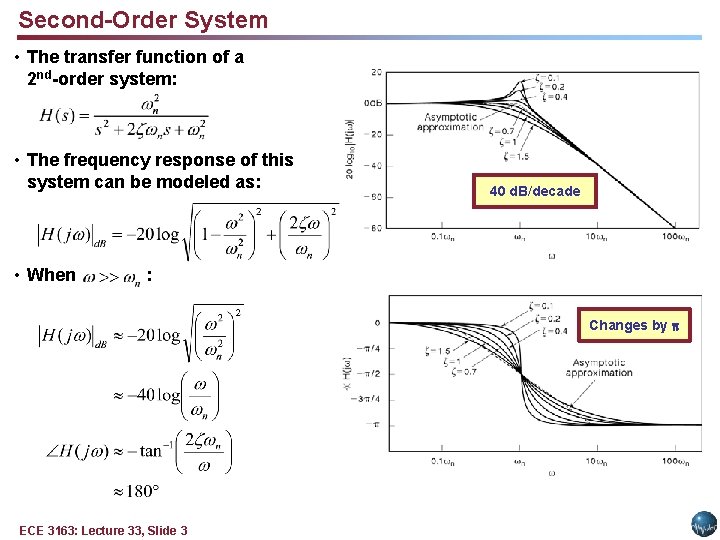
Second-Order System • The transfer function of a 2 nd-order system: • The frequency response of this system can be modeled as: • When 40 d. B/decade : Changes by ECE 3163: Lecture 33, Slide 3

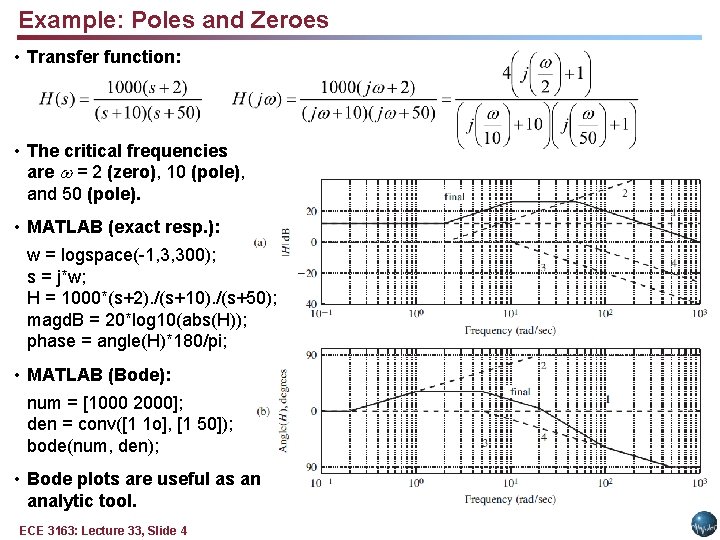
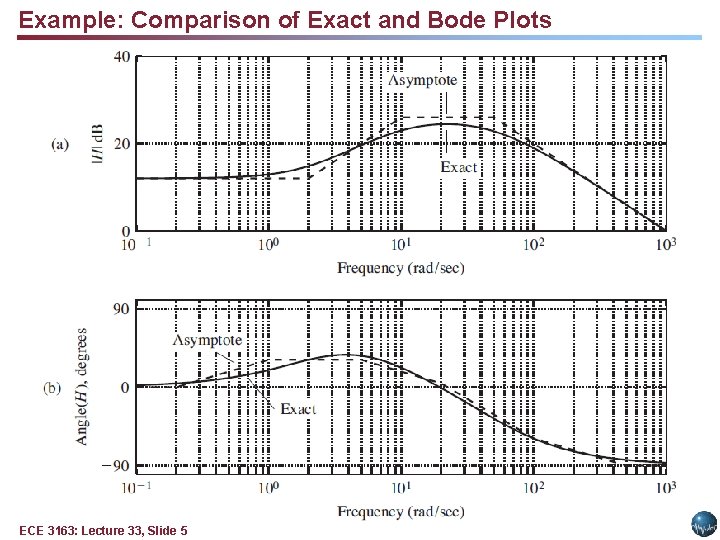
Example: Poles and Zeroes • Transfer function: • The critical frequencies are = 2 (zero), 10 (pole), and 50 (pole). • MATLAB (exact resp. ): w = logspace(-1, 3, 300); s = j*w; H = 1000*(s+2). /(s+10). /(s+50); magd. B = 20*log 10(abs(H)); phase = angle(H)*180/pi; • MATLAB (Bode): num = [1000 2000]; den = conv([1 1 o], [1 50]); bode(num, den); • Bode plots are useful as an analytic tool. ECE 3163: Lecture 33, Slide 4

Example: Comparison of Exact and Bode Plots ECE 3163: Lecture 33, Slide 5

Causal Filters • Recall that the ideal lowpass filter is a noncausal filter and hence unrealizable. • The filter design problem then becomes an optimization problem in which we try to best meet the user’s requirements with a filter that can be implemented with the least number of components. • This is equivalent to trying to minimize the number of coefficients in the (Laplace transform) transfer function. It is also comparable to minimizing the order of the filter. • Typically the numerator order is less than or equal to the denominator order, so, building on the concept of a Bode plot, we can relate the maximum amount of attenuation desired to the order of the denominator. • There are often no “perfect” solutions. Users must tradeoff design constraints such as passband smoothness, stopband attenuation and linearity in phase. • Computer-aided design programs, including MATLAB, are able to design filters once the user adequately specifies the constraints. We will explore two interesting analytic solutions: Butterworth and Chebyshev filters. ECE 3163: Lecture 33, Slide 6

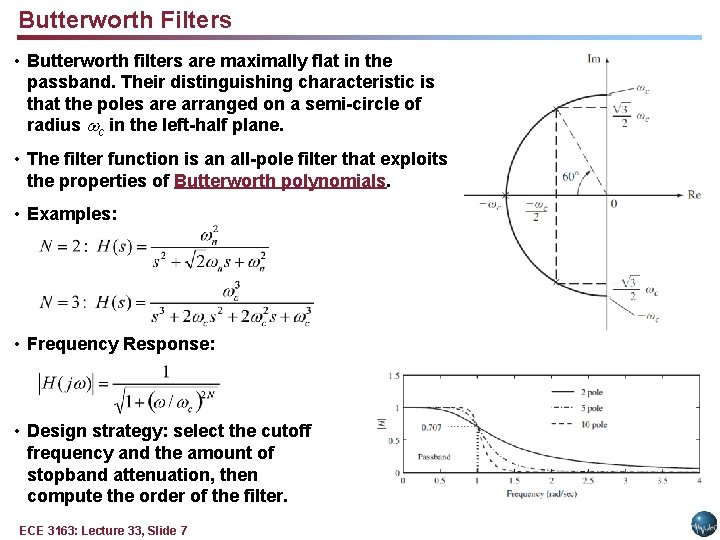
Butterworth Filters • Butterworth filters are maximally flat in the passband. Their distinguishing characteristic is that the poles are arranged on a semi-circle of radius c in the left-half plane. • The filter function is an all-pole filter that exploits the properties of Butterworth polynomials. • Examples: • Frequency Response: • Design strategy: select the cutoff frequency and the amount of stopband attenuation, then compute the order of the filter. ECE 3163: Lecture 33, Slide 7

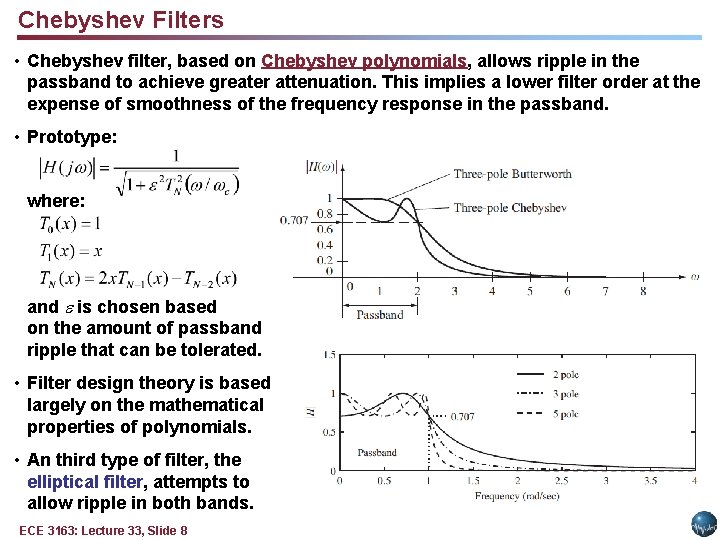
Chebyshev Filters • Chebyshev filter, based on Chebyshev polynomials, allows ripple in the passband to achieve greater attenuation. This implies a lower filter order at the expense of smoothness of the frequency response in the passband. • Prototype: where: and is chosen based on the amount of passband ripple that can be tolerated. • Filter design theory is based largely on the mathematical properties of polynomials. • An third type of filter, the elliptical filter, attempts to allow ripple in both bands. ECE 3163: Lecture 33, Slide 8

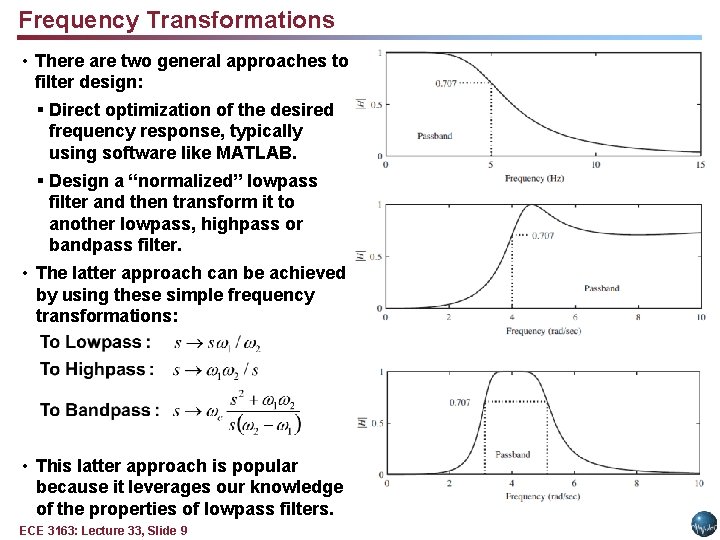
Frequency Transformations • There are two general approaches to filter design: § Direct optimization of the desired frequency response, typically using software like MATLAB. § Design a “normalized” lowpass filter and then transform it to another lowpass, highpass or bandpass filter. • The latter approach can be achieved by using these simple frequency transformations: • This latter approach is popular because it leverages our knowledge of the properties of lowpass filters. ECE 3163: Lecture 33, Slide 9

Summary • Analyzed the frequency response of a first and second-order system. • Demonstrated how this can be approximated using Bode plots. • Demonstrated that the Bode plot can be used to construct the frequency and phase responses of complex systems. • Introduced Butterworth and Chebyshev lowpass filters. • Described how lowpass filters can be converted to bandpass and highpass filters using a frequency transformation. ECE 3163: Lecture 33, Slide 10