ECCOMAS 2000 Barcelona Spain Sep 11 14 2000

ECCOMAS 2000 Barcelona, Spain, Sep. 11 -14, 2000 SIMPLIFIED ALGEBTAIC METHOD FOR COMPUTING EIGENPAIR SENSITIVITIES OF DAMPED SYSTEM *In-Won Lee 1), Sun-Kyu Park 2) and Hong-Ki Jo 3) 1) Professor, Department of Civil Engineering, KAIST 2) Professor, Department of Civil Engineering, Sung. Kyun. Kwan Univ. 3) Graduate Student, Department of Civil Engineering, KAIST

OUTLINE l INTRODUCTION l PREVIOUS STUDIES l PROPOSED METHOD l NUMERICAL EXAMPLE l CONCLUSIONS Structural Dynamics and Vibration Control Lab. , KAIST, Korea 2

l INTODUCTION • Objective of Study - To find the derivatives of eigenvalues and eigenvectors of damped systems with respect to design variables. • Applications of Sensitivity Analysis - Determination of the sensitivity of dynamic responses - Optimization of natural frequencies and mode shapes - Optimization of structures subject to natural frequencies. Structural Dynamics and Vibration Control Lab. , KAIST, Korea 3

• Problem Definition - Eigenvalue problem of damped system (1) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 4

- State space equation (2) - Orthonormalization condition (3) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 5

- Objective Given: Find: * indicates derivatives with respect to design variables (length, area, moment of inertia, etc. ) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 6

l PREVIOUS STUDIES • Z. Zimoch, “Sensitivity Analysis of Vibrating Systems, ” Journal of Sound and Vibration, Vol. 117, pp. 447 -458, 1987. (4) - restricted to lumped systems with distinct eigenvalues. Structural Dynamics and Vibration Control Lab. , KAIST, Korea 7

• Q. H. Zeng, “Highly Accurate Modal Method for Calculating Eigenvector Derivatives in Viscous Damping System, ” AIAA Journal, Vol. 33, No. 4, pp. 746 -751, 1995. (5) (6) - many eigenvectors are required to calculate eigenvector derivatives. Structural Dynamics and Vibration Control Lab. , KAIST, Korea 8

• Sondipon Adhikari, “Calculation of Derivative of Complex Modes Using Classical Normal Modes, ” Computer & Structures, Vol. 77, No. 6, pp. 625 -633, 2000. (7) - applicable only when the elements of C are small. Structural Dynamics and Vibration Control Lab. , KAIST, Korea 9

• I. W. Lee, D. O. Kim and G. H. Jung, “Natural Frequency and Mode Shape Sensitivities of Damped Systems: part I, Distinct Natural Frequencies, ” Journal of Sound and Vibration, Vol. 223, No. 3, pp. 399 -412, 1999. • I. W. Lee, D. O. Kim and G. H. Jung, “Natural Frequency and Mode Shape Sensitivities of Damped Systems: part II, Multiple Natural Frequencies, ” Journal of Sound and Vibration, Vol. 223, No. 3, pp. 413 -424, 1999. Structural Dynamics and Vibration Control Lab. , KAIST, Korea 10

Lee’s method (1999) (8) (9) - eigenvalue and eigenvector derivatives are obtained separately. Structural Dynamics and Vibration Control Lab. , KAIST, Korea 11

l PROPOSED METHOD • Rewriting basic equations - Eigenvalue problem (10) - Orthonormalization condition (11) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 12

• Differentiating eq. (10) with respect to design variable (12) • Differentiating eq. (11) with respect to design variable (13) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 13

• Combining eq. (12) and eq. (13) into a single matrix (14) - the coefficient matrix is symmetric and non-singular. - eigenpair derivatives are obtained simultaneously. Structural Dynamics and Vibration Control Lab. , KAIST, Korea 14
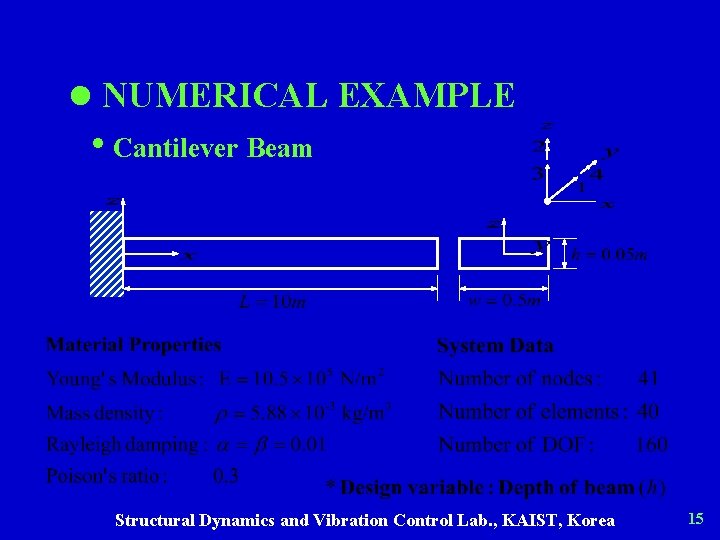
l NUMERICAL EXAMPLE • Cantilever Beam Structural Dynamics and Vibration Control Lab. , KAIST, Korea 15

• Analysis Methods • Lee’s method (1999) • Proposed method • Comparisons • Solution time (CPU) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 16
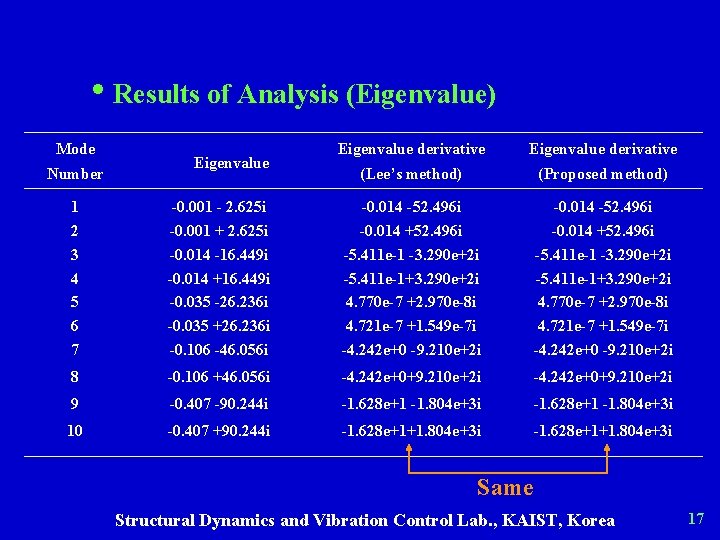
• Results of Analysis (Eigenvalue) Mode Number Eigenvalue derivative (Lee’s method) (Proposed method) 1 2 3 4 5 6 7 -0. 001 - 2. 625 i -0. 001 + 2. 625 i -0. 014 -16. 449 i -0. 014 +16. 449 i -0. 035 -26. 236 i -0. 035 +26. 236 i -0. 106 -46. 056 i -0. 014 -52. 496 i -0. 014 +52. 496 i -5. 411 e-1 -3. 290 e+2 i -5. 411 e-1+3. 290 e+2 i 4. 770 e-7 +2. 970 e-8 i 4. 721 e-7 +1. 549 e-7 i -4. 242 e+0 -9. 210 e+2 i 8 -0. 106 +46. 056 i -4. 242 e+0+9. 210 e+2 i 9 -0. 407 -90. 244 i -1. 628 e+1 -1. 804 e+3 i 10 -0. 407 +90. 244 i -1. 628 e+1+1. 804 e+3 i Same Structural Dynamics and Vibration Control Lab. , KAIST, Korea 17
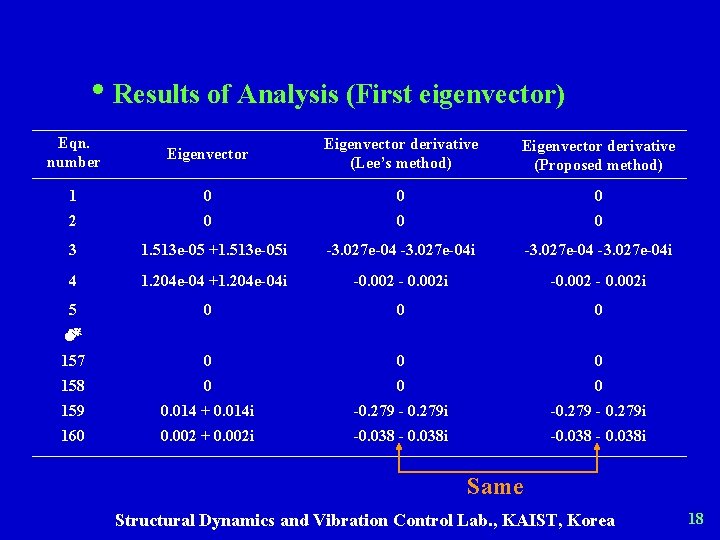
• Results of Analysis (First eigenvector) Eqn. number Eigenvector derivative (Lee’s method) Eigenvector derivative (Proposed method) 1 0 0 0 2 0 0 0 3 1. 513 e-05 +1. 513 e-05 i -3. 027 e-04 i 4 1. 204 e-04 +1. 204 e-04 i -0. 002 - 0. 002 i 0 0 0 157 0 0 0 158 0 0 0 159 0. 014 + 0. 014 i -0. 279 - 0. 279 i 160 0. 002 + 0. 002 i -0. 038 - 0. 038 i 5 Same Structural Dynamics and Vibration Control Lab. , KAIST, Korea 18
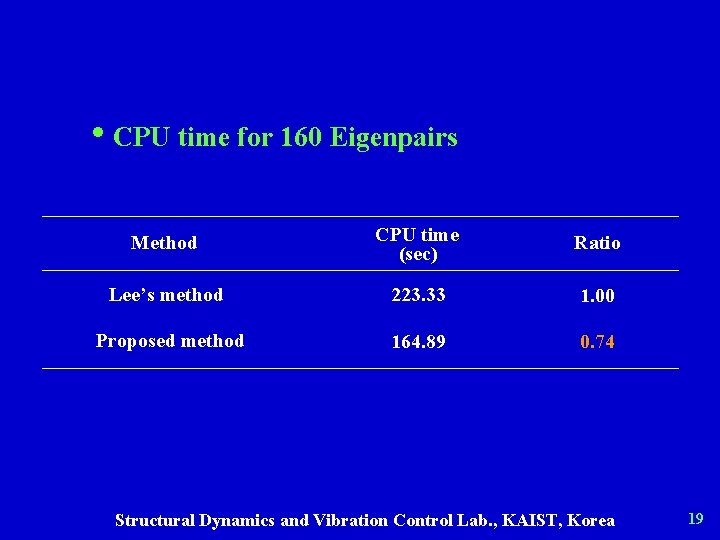
• CPU time for 160 Eigenpairs Method CPU time (sec) Ratio Lee’s method 223. 33 1. 00 Proposed method 164. 89 0. 74 Structural Dynamics and Vibration Control Lab. , KAIST, Korea 19
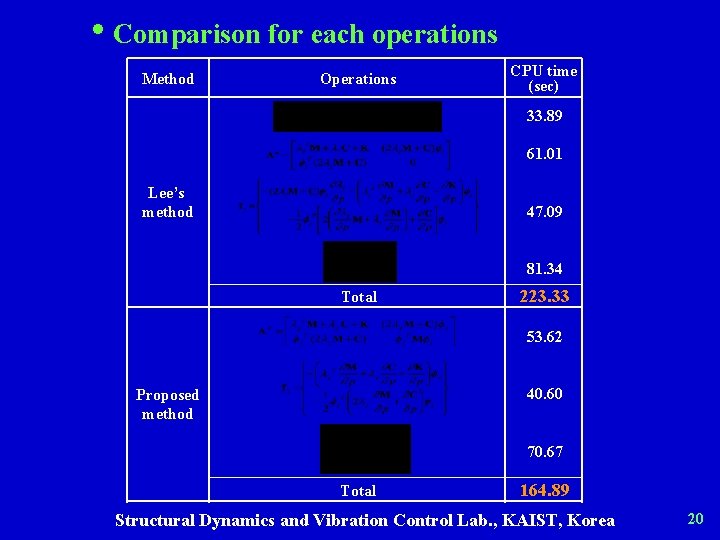
• Comparison for each operations Method Operations CPU time (sec) 33. 89 61. 01 Lee’s method 47. 09 81. 34 Total 223. 33 53. 62 40. 60 Proposed method 70. 67 Total 164. 89 Structural Dynamics and Vibration Control Lab. , KAIST, Korea 20

l CONCLUSIONS • Proposed method - is simple - guarantees numerical stability - reduces the CPU time. An efficient eigensensitivity technique ! Structural Dynamics and Vibration Control Lab. , KAIST, Korea 21

Thank you for your attention. Structural Dynamics and Vibration Control Lab. , KAIST, Korea 22

l APPENDIX • Numerical Stability • The determinant property (15) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 23

Then (16) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 24

Arranging eq. (16) (17) Using the determinant property of partitioned matrix (18) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 25

Therefore (19) Numerical Stability is Guaranteed. Structural Dynamics and Vibration Control Lab. , KAIST, Korea 26

• Lee’s method (1999) • Differentiating eq. (1) with respect to design variable (20) • Pre-multiplying each side of eq. (20) by eigenvalue derivative. gives (21) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 27

• Differentiating eq. (3) with respect to design variable (22) • Combining eq. (20) and eq. (22) into a matrix gives eigenvector derivative. (23) Structural Dynamics and Vibration Control Lab. , KAIST, Korea 28
- Slides: 28