Ecarttype et variance RAPPELS STATISTIQUES Echantillon reprsentatif Moyenne

Ecart-type et variance RAPPELS STATISTIQUES • Echantillon représentatif • Moyenne • Espérance • Pas beaucoup d’information… [8 9 11 12] et [0 5 15 20] → même moyenne 1

Ecart-type et variance RAPPELS STATISTIQUES • Ecart moyen entre les valeurs d’un ensemble : écart-type ou • Variance = carré de l’écart-type Si E(X)=0 : 2

Covariance RAPPELS STATISTIQUES • Mesure de la variation simultanée de deux variables aléatoires • Si v. a. discrètes: 3

Matrice de covariance RAPPELS STATISTIQUES • Espaces à dimension > 2 : covariance de ces variables deux à deux – Exemple à 3 dimensions : • Matrice symétrique car : 4

Valeur propre et vecteur propre RAPPELS ALGEBRE MATRICIEL • Valeur propre l d’une matrice carrée A : • Propriétés : – λ est une valeur propre de A ssi – Si l est une valeur propre de A, alors toute solution x≠ 0 de est un vecteur propre associé 5

PCA : kesaco? • « Principal Components Analysis » • Représenter une variable à "p" paramètres dans un espace à "n" dimensions (n<p) • Minimiser la perte d’information par un changement de base • Critères de « représentativité » d’un axe – Variance généralement 6

PCA : théorie • X un vecteur de v. a. de dimension m (m paramètres) • Supposons espérance de X = 0 • Nous avons donc : 7

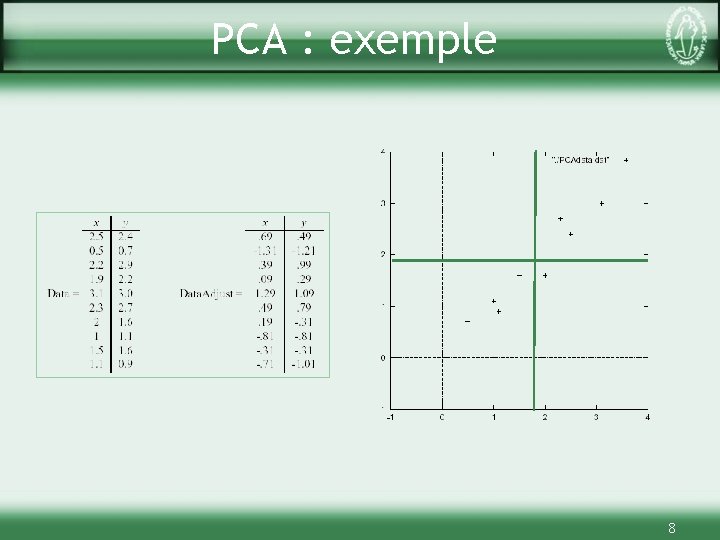
PCA : exemple 8

PCA : théorie • But : changement de base – Trouver la (les) dimension(s) supprimable(s) – Base → Besoin de vecteurs orthonormés • Soit q un de ces vecteurs – Projection sur ce vecteur (A = « projection » ) : avec • De plus : puisque E[X] = 0 9

PCA : théorie • Variance du vecteur A : car CECI car AT = q. TX= XTq • R (m x m) = matrice de covariance des v. a. composant le vecteur X 10

PCA : exemple • Calculons la matrice de covariance : 11

PCA : théorie • R = matrice de covariance, donc : Or R est symétrique ssi: a, b sont des vecteurs m x 1 Et donc : • La variance de A est fonction du vecteur q : Ψ est une « sonde à variance » selon l’axe 12

PCA : théorie • Le problème est donc : Trouver les q tels que ψ(q) est extremum car • De plus, nous avons : 13

PCA : théorie • En ignorant les termes de second ordre et connaissant la définition de ψ : • Nous pouvons donc déduire, grâce au transparent précédent : • De plus : → la perturbation δq est orthogonale à q (donc ne fait pas varier la norme de q) 14

PCA : théorie • Nous pouvons maintenant écrire : ou, de façon équivalente : où λ est un facteur scalaire • Ce qui nous oblige à avoir : • Permet de trouver les q tels que ψ(q) extremum – Les solutions non-triviales (q≠ 0) sont les valeurs propres – Les vecteurs q sont les vecteurs propres 15

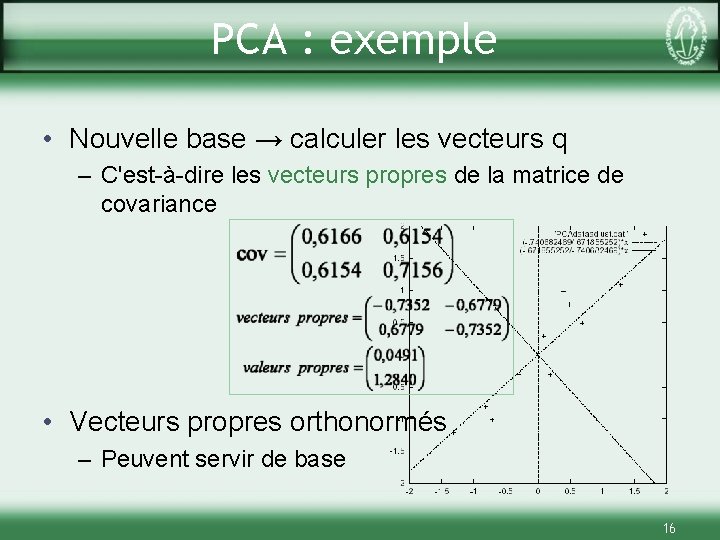
PCA : exemple • Nouvelle base → calculer les vecteurs q – C'est-à-dire les vecteurs propres de la matrice de covariance • Vecteurs propres orthonormés – Peuvent servir de base 16

PCA : théorie • Reste à savoir la valeur de ψ pour chaque q! • Distinguons les λ et les q par des indices : • Supposons les λ numérotés tels que : et donc λ 1 = λmax • Construisons une matrice m x m définie par : 17

PCA : théorie • Nous pouvons réécrire les m équations : où Λ est une matrice diagonale définie par les valeurs propres de R : • Q est une matrice orthogonale c'est-à-dire : car ses colonnes vérifient : 18

PCA : théorie • Et donc : • Dès lors, l’équation peut s’écrire : • De cette dernière équation et de la définition de la fonction ψ on trouve que : 19

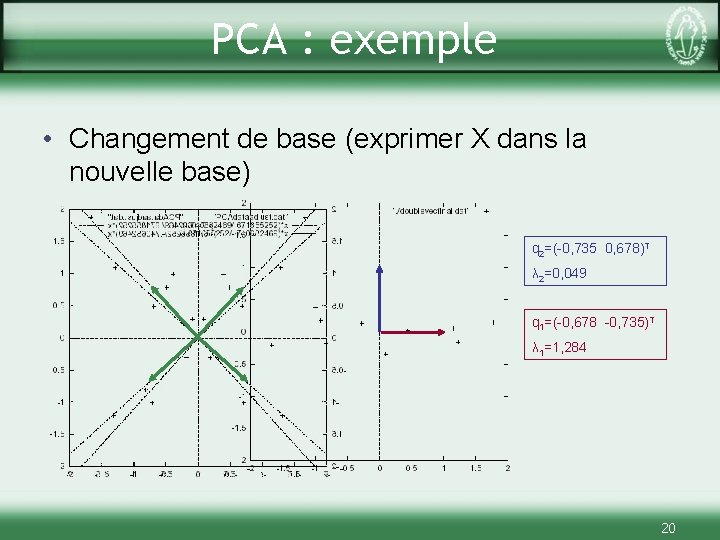
PCA : exemple • Changement de base (exprimer X dans la nouvelle base) q 2=(-0, 735 0, 678)T λ 2=0, 049 q 1=(-0, 678 -0, 735)T λ 1=1, 284 20

PCA : théorie RECONSTRUCTION DES DONNEES • Soit x une réalisation du vecteur X – m vecteurs de base, m projections à considérer Les vecteurs aj sont appelés les composantes principales • Pour reconstruire les données : 21

PCA : théorie REDUCTION DE DIMENSIONS • Tronquer le vecteur de données x – λ 1 , λ 2, …, λl sont les + grandes valeurs propres – Ignorer les dimensions l+1, …, m Décodage • De plus, comme précédemment : Encodage 22

PCA : théorie ENCODAGE -DECODAGE • En résumé : – Encodage Le vecteur d’erreur vaut : encodeur – Décodage décodeur 23

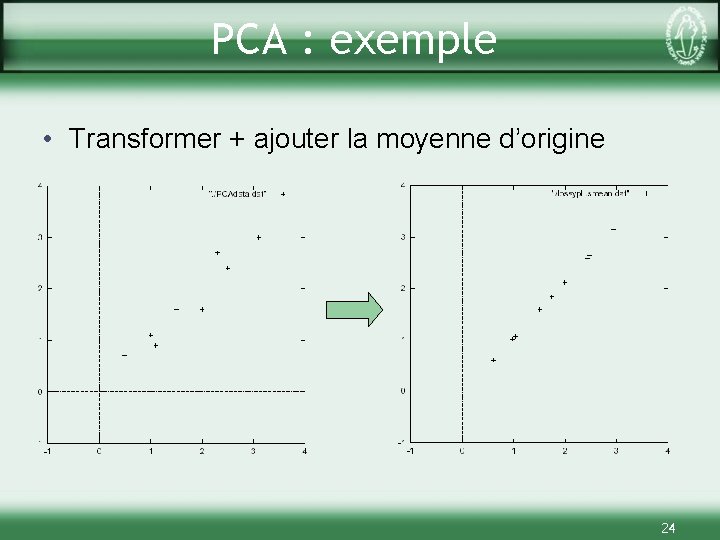
PCA : exemple • Transformer + ajouter la moyenne d’origine 24

PCA : applications COMPRESSION D’IMAGES : METHODE DE BASE • Images en niveaux de gris – Chaque pixel = nombre entre 0 et 255 • Diviser l’image en carrés de n pixels de côté – Chaque carré est un échantillon (un « individu » ) – n² paramètres 25

PCA : applications COMPRESSION D’IMAGES : METHODE DE BASE • Exemple précédent : – Image 256 x 256 – Carrés 8 x 8 → 1024 « individus » (vecteurs) → 64 « critères » (dimensions) • Retirer le vecteur moyenne à chaque «individu» • Calculer la matrice de covariance (64 x 64) • Calculer valeurs propres et vecteurs propres 26

PCA : applications COMPRESSION D’IMAGES : METHODE DE BASE • Changement de base : Variance • Élimination des dimensions moins significatives • Décodage : 27

PCA : applications COMPRESSION DE PLUSIEURS IMAGES ET D’IMAGES MULTICANAUX • Supposons i images, chacune de n² pixels • Création de n² vecteurs de i paramètres • Chaque vecteur = intensités d’un pixel donné sur chaque image traitée • Idéal pour le traitement d’images « multicanaux » : images en couleurs (3 canaux) ou images satellites. x x 2 3 x 1 28

PCA : applications COMPRESSION DE PLUSIEURS IMAGES ET D’IMAGES MULTICANAUX Première composante Seconde composante 29

PCA : applications COMPRESSION DE PLUSIEURS IMAGES ET D’IMAGES MULTICANAUX Troisième composante Quatrième composante 30

PCA : applications COMPRESSION DE PLUSIEURS IMAGES ET D’IMAGES MULTICANAUX Cinquième composante Sixième composante 31

PCA et les réseaux de Hebb PREREQUIS : APPRENTISSAGE PAR LA REGLE DE HEBB «Quand un axone de la cellule A est suffisamment proche pour exciter «When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or la cellule B de façon répétitive ou persistante, il se produit un metabolic changes processus de croissance take place ou un in changement one or both métabolique cells such that tel que A’s efficiency as one of the cells firing B, is increased. » l’efficacité de A, en tant que cellule excitant B s’en trouve augmentée. » 1. Si deux neurones de part et d’autre d’un synapse (connexion) sont activés simultanément(d’une manière synchrone), alors la force de ce synapse doit être augmentée ; 2. Si les mêmes deux neurones sont activés d’une manière asynchrone, alors le synapse correspondant doit être affaibli ou carrément éliminé. 32

PCA et les réseaux de Hebb PREREQUIS : APPRENTISSAGE PAR LA REGLE DE HEBB • Forme simple de la règle de Hebb : où y(n) est la sortie du neurone au pas n, xj(n) est le stimulus à l’entrée j et wj(n) est le poids synaptique de l’entrée j. η est une constante positive qui détermine le taux d’apprentissage • Forme vectorielle : • Problème : – Signal d’entrée xj répété amène une augmentation de y – Augmentation exponentielle → saturation de la connexion 33

PCA et les réseaux de Hebb PREREQUIS : APPRENTISSAGE PAR LA REGLE DE HEBB • Solutions 1. Facteur d’oubli – Retrancher une portion du poids actuel à la variation de poids : où 0 ≤ α ≤ 1 – Nouveau problème : peu de stimuli → oubli de l’appris! – Une des solutions Si α= η, règle « instar » 34

PCA et les réseaux de Hebb PREREQUIS : APPRENTISSAGE PAR LA REGLE DE HEBB • Solutions 2. Normalisation de W 35

PCA et les réseaux de Hebb APPROCHE A 1 NEURONE • Problème de divergence avec Hebb – Règle de Oja : approche en série de puissance de la forme normalisée de W Pour des petits η le terme O(η²) peut être ignoré Input « effectif » dépendant des poids et de la sortie 36

PCA et les réseaux de Hebb APPROCHE A 1 NEURONE • Variation de poids au temps n: • Calculons son espérance : • Dans le cas d’un neurone linéaire : • Donc : 37

PCA et les réseaux de Hebb APPROCHE A 1 NEURONE • C est la matrice de covariance de X • Lors de la convergence : • Et donc, à la convergence : • Par définition, λ est une valeur propre de C • W est le vecteur propre associé à λ et : W est un vecteur normalisé 38

PCA et les réseaux de Hebb APPROCHE A 1 NEURONE • Finalement : – W est normé et valeur propre de la matrice de covariance C du vecteur X → WTX = XTW est une composante principale de X – De plus, on peut montrer (mais pas ici…) que la valeur propre associée à W calculé de cette manière est la plus grande valeur propre de C → WTX est la première composante principale de X – Comment calculer les autres? • Plusieurs neurones linéaires → plusieurs sorties • Règle de Sanger pour généraliser Oja 39

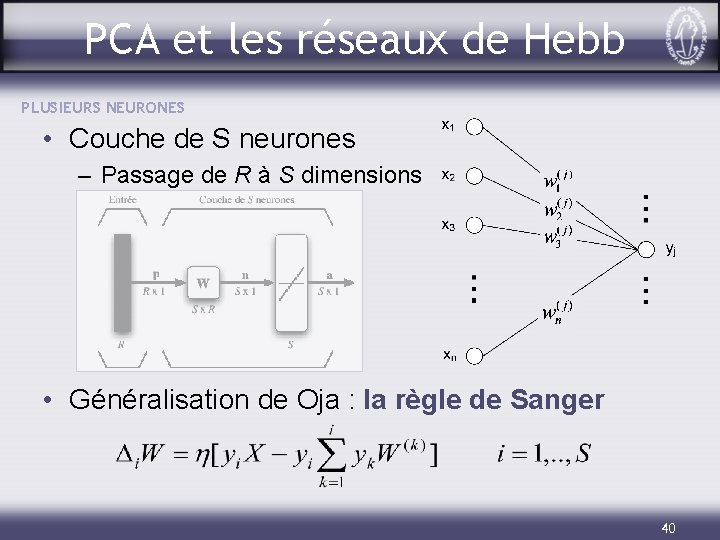
PCA et les réseaux de Hebb PLUSIEURS NEURONES • Couche de S neurones – Passage de R à S dimensions • Généralisation de Oja : la règle de Sanger 40

PCA et les réseaux de Hebb PLUSIEURS NEURONES • En effet, si i=1, on retrouve la règle de Oja : • Réécrivons la règle de Sanger : où : • Pour i=1, nous avons donc X=X’ • Pour i=2, nous obtenons : 41

PCA et les réseaux de Hebb PLUSIEURS NEURONES • Donc, supposant que le premier neurone a déjà convergé : – on enlève de X une fraction y 1 de la première composante principale – la première composante principale du vecteur X’ est équivalente à la seconde de X • Pour le troisième neurone : • En pratique, tous les neurones tendent à converger ensemble… 42

PCA et les réseaux de Hebb PLUSIEURS NEURONES • Notation matricielle : LT[. ] est un opérateur qui met à 0 tous les termes au dessus de la diagonale de la matrice qu’il contient • Exemple d’application : 43

PCA et les réseaux de Hebb PLUSIEURS NEURONES : APEX • Variante de l’algorithme : adaptive principal component extraction (APEX) – connexions latérales pour exprimer l'influence d'un neurone sur les suivants – plus compliqué à calculer mais converge apparemment plus rapidement… 44