EC 941 Game Theory Lecture 2 Prof Francesco

EC 941 - Game Theory Lecture 2 Prof. Francesco Squintani Email: f. squintani@warwick. ac. uk 1

Structure of the Lecture n Mixed Strategies n Nash Equilibrium and Rationalizability n Correlated Equilibrium 2

Mixed Strategies In a game in strategic form G=(I, S, u), for each player i, Si is the set of pure strategies. A mixed strategy si is a probability distribution over Si. When playing si , player i operates a randomizing device and chooses the strategy accordingly. For example, she flips a coin choosing one strategy if 3

In general, randomizing devices can be very complex and induce any probability distribution. Payoffs and best-response correspondences can be extended from pure strategies to mixed strategies. Solution concepts (Nash Equilibrium, Dominance and Rationalizability) can be extended to mixed strategies. To play a mixed strategy si, player i must be indifferent among the possible pure strategies. This indifference principle is crucial to calculate solutions. 4

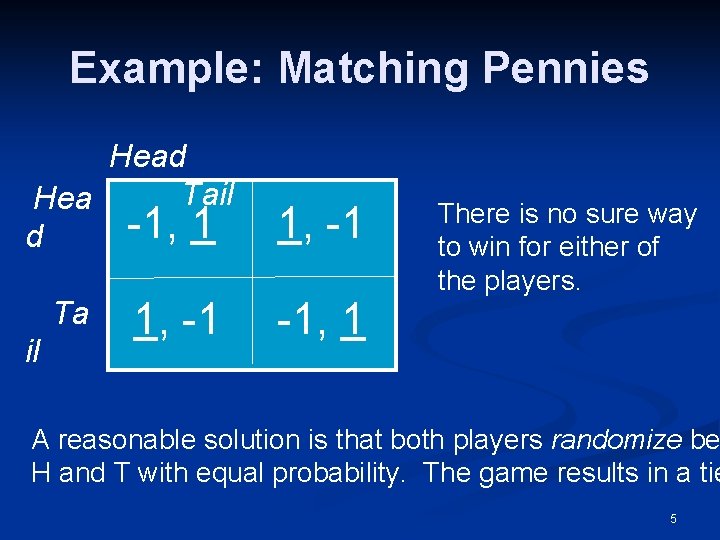
Example: Matching Pennies Head Tail Hea -1, 1 d Ta il 1, -1 -1, 1 There is no sure way to win for either of the players. A reasonable solution is that both players randomize be H and T with equal probability. The game results in a tie 5

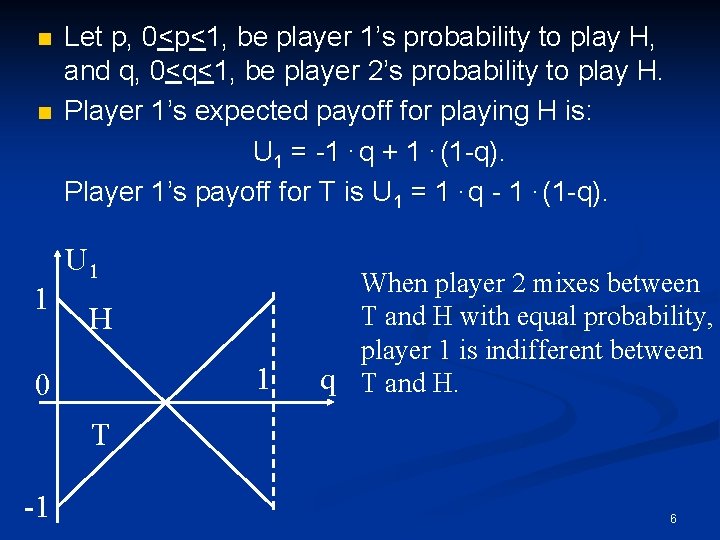
n n 1 Let p, 0<p<1, be player 1’s probability to play H, and q, 0<q<1, be player 2’s probability to play H. Player 1’s expected payoff for playing H is: U 1 = -1. q + 1. (1 -q). Player 1’s payoff for T is U 1 = 1. q - 1. (1 -q). U 1 H 1 0 When player 2 mixes between T and H with equal probability, player 1 is indifferent between q T and H. T -1 6

We can write best response correspondences in terms of mixed strategy: B 1(q) = 1 if q < ½ B 2(p) = 0 if p < ½ B 1(q) = [0, 1] if q = ½ B 2(p) = [0, 1] if p =½ B 1(q) = 0 if q > ½ B 2(p) = 1 if p q > ½. The Nash Equilibrium is 1 B (p) found by intersecting the 2 Best Response ½ correspondences. n B 1(q) 0 ½ 1 p The Nash Equilibrium is (p, q) = (½, ½). 7

General Definitions Consider a game in strategic form G = (I, S, u). Definition A mixed strategy si of a player i is a probability distribution over player i’s pure strategies Si. The set of all player i’s possible mixed strategies is Si ={(si (si)) : si (si) > 0 for all si, and Ss si (si) = 1}. 8

Definition When the players play the mixed strategy profile s, player i’s expected payoff Ui is: Ui (s) = Ss [ Pi si (si) ] ui (s). Definition The mixed strategy extension of G is a game in strategic form G = (I, S, U). Note The mixed strategies S of the game G are the pure strategies of game G. Best Response Correspondences, Nash Equilibrium, Dominance and Rationalizability can be defined for game G. 9

The mixed strategy profile s∗ is a Nash equilibrium if, for each player i, Ui(s∗) ≥ Ui(si, s∗−i) for every mixed strategy si of player i. n n n For every player i, the best response correspondence is Bi (s−i) = {si : Ui(si, s−i) ≥ Ui(s’i, s−i) for every s’i}. The profile s∗ is a Nash equilibrium if and only if s∗i belongs to Bi (s∗−i), for every i. 10

Proposition If player i’s strategy si is strictly dominated, then any mixed strategy si which assigns strictly positive probability to si is also strictly dominated. The definition of rationalizability follows from the iterated deletion of strictly dominated strategies. Given a game G = (I, S, U), let Xi 1 = Si. For each t = 0, . . . , T − 1, Xit+1 is a subset of Xit such that every si in Xit that is not in Xit+1 is strictly dominated 11

The Indifference Principle. If the opponents play s−i, player i is indifferent among all pure strategies in the best response set Bi (s−i). Definition For any si, let Ci(si) be the support of si, the set of strategies si to which si assigns non-zero probability. * 12

In games with 2 players and 2 strategies for each player (let A 1 = {U, D} and A 2 = {L, R}), we find the completely mixed strategy Nash equilibrium as follows. From the indifference condition for player 1: s. L u 1(U, L) + (1 - s. L) u 1(U, R) = s. L u 1(D, L) + (1 - s. L) u 1(D, R) we find the mixed strategy s. L. s. U u 2(U, L) + (1 -s. U) u 2(D, L) = s. U u 2(U, R) + (1 -s. U) u 2(D, R) 13

Definition For any player i, and (non-empty) subset Bi of the strategy set Si, let S−i (Bi) be the set of mixed strategy profiles s−i such that Bi = Bi(s−i). We can find all mixed strategy equilibria as follows. Consider each profile B of subsets Bi, and calculate the profile (S−i (Bi))I. The mixed strategy s is a Nash Equilibrium if: 1. s belongs to S (B ) for all players i. 14

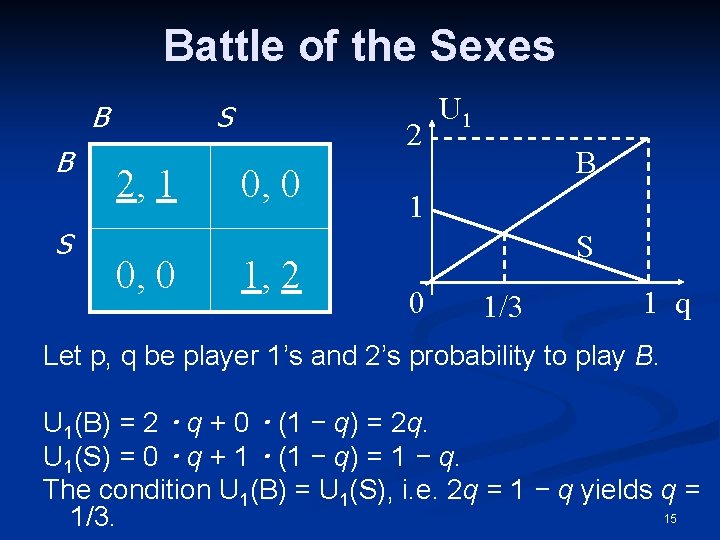
Battle of the Sexes B B S S 2, 1 0, 0 2 0, 0 1, 2 U 1 B 1 S 0 1/3 1 q Let p, q be player 1’s and 2’s probability to play B. U 1(B) = 2・q + 0・(1 − q) = 2 q. U 1(S) = 0・q + 1・(1 − q) = 1 − q. The condition U 1(B) = U 1(S), i. e. 2 q = 1 − q yields q = 15 1/3.

U 2(B) = 1・p + 0・(1 − p) = p. U 2(S) = 0・p + 2・(1 − p) = 2 − 2 p. The condition U 2(B) = U 2(S), yields p = 2/3. B 1 (q) = 0 if q < 1/3 B 1 (q) = [0, 1] if q = 1/3 B 1 (q) =1 if q > 1/3 B 2 (p) = 0 if p < 2/3 B 2 (p) = [0, 1] if p = 2/3 B 2 (p) =1 if p > 2/3 q 1 B 2(p) B 1(q) 1/3 0 2/3 1 p 16

The game has three mixed strategy Nash equilibria: (p, q) = (0, 0), (2/3, 1/3), and (1, 1). The mixed strategy equilibria (0, 0) and (1, 1) correspond to the two pure strategy equilibria. The expected payoff of the equilibrium (2/3, 1/3) is U 1 = 2 ・ 2/9 + 0・ 4/9 + 0・ 1/9 + 1・ 2/9 = 2/3. Likewise, U 2 = 2/3. So, it is Pareto dominated by both pure strategy equilibria, which yield payoffs (2, 1) and (1, 2). 17

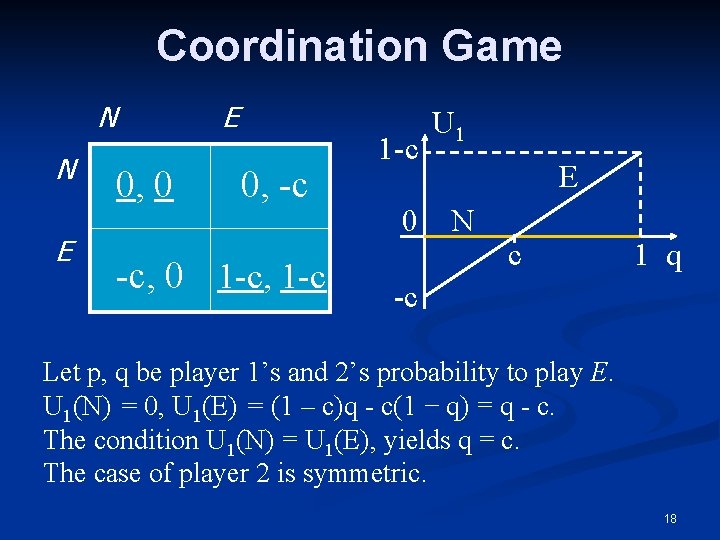
Coordination Game N N E E 0, 0 0, -c -c, 0 1 -c, 1 -c 0 U 1 E N c 1 q -c Let p, q be player 1’s and 2’s probability to play E. U 1(N) = 0, U 1(E) = (1 – c)q - c(1 − q) = q - c. The condition U 1(N) = U 1(E), yields q = c. The case of player 2 is symmetric. 18

B 1(q) = 0 if q < c B 1(q) = [0, 1] if q = c B 1(q) =1 if q > c B 2(p) B 1(q) B 2(p) = 0 if p < c B 2(p) = [0, 1] if p = c B 2(p) =1 if p > c 0 c 1 p The game has three mixed strategy Nash equilibria: (p, q) = (0, 0), (c, c), and (1, 1). The mixed strategy equilibria (0, 0) and (1, 1) correspond to the pure strategy equilibria (N, N) and (E, E). The expected payoff of the equilibrium (c, c) is 19

Games with Dominated Strategies 2 D E F A 2, 1 0, 2 4, 1 B 1, 3 3, 1 3, 0 C 1, 1 2, 2 1 Strategy C is dominated by any mixed strategy a 1 with 0 < a 1(A) < 2/3. Once C is deleted, strategy F is dominated by E. 20

D E F 2 A 2, 1 0, 2 4, 1 B 1, 3 3, 1 3, 0 C 1, 1 2, 2 1 The set of rationalizable strategies is {A, B} and {D, E}. Inspection of the best response correspondence shows that there are no pure-strategy Nash Equilibria. 21

D E F 2 A 2, 1 0, 2 4, 1 B 1, 3 3, 1 3, 0 C 1, 1 2, 2 1 With the indifference principle, we find completely mixed strategy N. E. in the game reduced to {A, B}X{D, E}. Player 1 is indifferent between A and B when 2 s 2(D) = s 2(D) + 3[1 - s 2(D)] i. e. , when s 2(D) = 3/4. 22

D E F 2 A 2, 1 0, 2 4, 1 B 1, 3 3, 1 3, 0 C 1, 1 2, 2 1 Player 2 is indifferent between D and E when s 1(A)+3[1 -s 1(A)]=2 s 1(A)+[1 -s 1(A)] i. e. , when s 1(A)=2/3. The unique Nash Equilibrium of the game has C(s)={A, B}X{D, E} with s 1(A)=2/3 and s 2(D) = 3/4. 23

E F G H A 0, 3 1, 0 0, 2 0, 4 B 3, 1 2, 2 1, 1 C 4, 0 1, 1 2, 2 0, 1 D 2, 5 1, 4 0, 2 3, 1 1 First, we iteratively delete strictly dominated strategies. In the first round, only strategy A is deleted. 24

E F G H 2 A 0, 3 1, 0 0, 2 0, 4 B 3, 1 2, 2 1, 1 C 4, 0 1, 1 2, 2 0, 1 D 2, 5 1, 4 0, 2 3, 1 1 After deleting A, strategy H is strictly dominated. H is the only strategy deleted in the second round. 25

E F G H 2 A 0, 3 1, 0 0, 2 0, 4 B 3, 1 2, 2 1, 1 C 4, 0 1, 1 2, 2 0, 1 D 2, 5 1, 4 0, 2 3, 1 1 3 After deleting H, strategy D is strictly dominated. D is the only strategy deleted in the third round. 26

E 4 F G H 2 A 0, 3 1, 0 0, 2 0, 4 B 3, 1 2, 2 1, 1 C 4, 0 1, 1 2, 2 0, 1 D 2, 5 1, 4 0, 2 3, 1 1 3 After deleting D, strategy E is strictly dominated. E is the only strategy deleted in the third round. The remaining strategies {B, C}, {F, G} cannot be deleted. 27

E 4 F G H 2 A 0, 3 1, 0 0, 2 0, 4 B 3, 1 2, 2 1, 1 C 4, 0 1, 1 2, 2 0, 1 D 2, 5 1, 4 0, 2 3, 1 1 3 Inspection of best responses shows that (B, F) and (C, G) are pure-strategy Nash Equilibria. We find mixed strategy N. E. in the game on {B, C}X{F, G}. 28

E 4 F G H 2 A 0, 3 1, 0 0, 2 0, 4 B 3, 1 2, 2 1, 1 C 4, 0 1, 1 2, 2 0, 1 D 2, 5 1, 4 0, 2 3, 1 1 3 Player 1 is indifferent between B and C when 2 s 2(F) + [1 -s 2(F)] = 2[1 -s 2(F)] + s 2(F), i. e. s 2(F)=1/2. By symmetry, player 2 is indifferent when s 1(A)=1/2. 29

A Game with Many Players n n people observe a crime. n Each attaches the value v to the police being informed and bears the cost c if calling the police, where v > c > 0. n There are n pure strategy equilibria. n In each one of these equilibria, a player i reports, and the remaining n - 1 players do not. 30

n Let p be the mixed strategy that a player calls the police. n The symmetric mixed strategy equilibrium p is determined by the indifference condition: v − c = 0・Pr{no one else calls} + v・Pr{someone else calls} v − c = v・(1 - Pr{no one else calls}) v − c = v・(1 – p) n-1) or c = – v (1 – p) n-1 p = 1 − (c/v)1/(n− 1) 31

Correlated Equilibrium: Example Dove Hawk 0, 0 -2, 1 1, -2 -3, -3 In the hawk-dove game, two States confront in a dispute. If a State plays Dove and the other Hawk, the Dove loses the dispute. But if both States are Hawks, a war takes place. 32

Dove Hawk 0, 0 -2, 1 Hawk 1, -2 -3, -3 There are two pure-strategy Nash Equilibria (H, D) and (D, H), with payoffs (1, -2) and (-2, 1). There is a mixed strategy Nash equilibrium s(D) = 1/2, which yields payoff of -1 to both players. 33

If the players can play (H, D) and (D, H) with equal probability, their expected payoff is -1/2. Playing the Nash equilibria (H, D) and (D, H) with equal probability, is a correlated equilibrium. The players coordinate on a different Nash equilibrium on the basis of a fair coin toss. The coin is the correlating device. Can the players achieve a higher payoff with a more complex correlating device? 34

Suppose that they resort to a mediator: 1. The mediator randomly chooses between one of the four outcomes (H, H), (H, D), (D, H), and (D, D) using the probability profile p = (p. HH, p. HD, p. DH, p. DD). 2. The mediator does not report her choice. She makes a separate, private recommendation h or d, to each one of the players. For example, if her choice is (H, D), she recommends h to player 1 and d to player 2. The probability profile p is a correlated equilibrium if all the private recommendations are self-enforcing. 35

For player 1, the private recommendation d is selfenforcing if U 1(D|d) = u 1(D, D)p(DD|d) + u 1(D, H)p(DH|d) > U 1(H|d) = u 1(H, D)p(DD|d) + u 1(H, H)p(DH|d) and the private recommendation h is self-enforcing if: U 1(H|h) = u 1(H, D)p(HD|h) + u 1(H, H)p(HH|h) > U 1(D|h) = u 1(D, D)p(HD|h) + u 1(D, H)p(HH|h) and the conditions for player 2 are analogous. 36

To find the symmetric correlated equilibrium which maximizes the sum of payoffs, we solve the program: max [u 1(D, D)+u 2(D, D)]p(DD)+[u 1(D, H)+u 2(D, H)]p(DH) +[u 1(H, D)+u 2(H, D)]p(HD)+[u 1(H, H)+u 2(H, H)]p(HH) s. t. Ui(D|d) > Ui(H|d) Ui(D|h) > Ui(H|h) p(DH) = p(HD) for both players i = 1, 2. 37

Substituting in the payoffs, and using symmetry, we obtain: U 1(D|d) = -2 p(DH|d) > U 1(H|d) = p(DD|d) - 3 p(DH|d) U 1(H|h) = p(HD|h) - 3 p(HH|h) > U 1(D|h) = -2 p(HH|h). Expanding the conditional probabilities, and simplifying -2 p(DH) > p(DD) - 3 p(DH) p(HD) - 3 p(HH) > -2 p(HH). Note that this is a set of linear inequalities. 38

We solve for the optimal correlated equilibrium: max 0 p(DD)+2(1 -2)p(DH) - 6 p(HH) s. t. p(DH) = p(HD) -2 p(DH) > p(DD) -3 p(DH) p(HD) -3 p(HH) > -2 p(HH) Simplifying, we obtain: p(DH) = p(HD) > p(DD) and p(HD) = p(DH) > p(HH). The solution is p(HH)=0, p(HD)=p(DH)=p(DD)=1/3. The expected payoff of both players i = 1, 2 is: Ui(p) = 0 p(DD) + p(HD) - 2 p(DH) = -1/3. 39

Correlated Equilibrium Definition A correlated equilibrium in a game G=(I, S, u) is a probability distribution p over the set S such that, for any player i, and all her strategies si Ss-i [ui (si, s-i) p(si, s-i)] > Ss-i [ui (s’i, s-i) p(s’i, s-i)], for all s’i. Proposition Any correlated equilibrium is also a mixed strategy Nash Equilibrium. 40

Summary of the Lecture n Mixed Strategies n Nash Equilibrium and Rationalizability n Correlated Equilibrium 41

Preview Next Lecture n Bayesian Games and Nash Equilibrium n Bayesian Games and Information n Cournot Duopoly with Private Information n Public Good Provision with Private Information 42