EARTHQUAKES 2 WAVEFORM MODELING MOMENT TENSORS SOURCE PARAMETERS

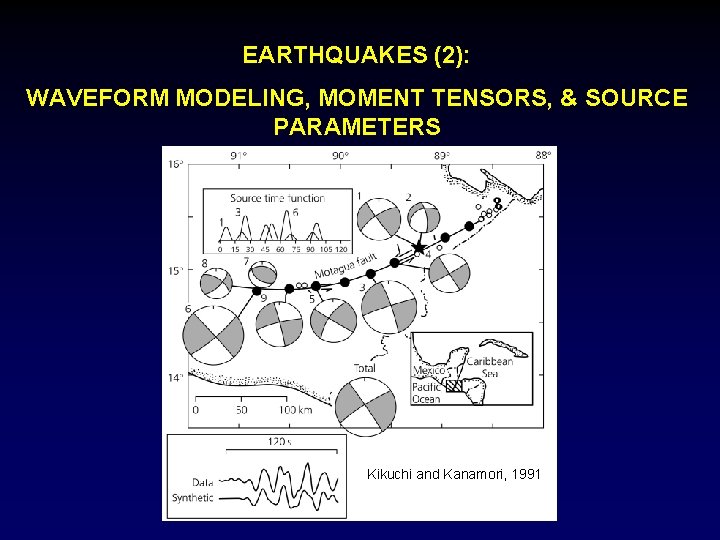
EARTHQUAKES (2): WAVEFORM MODELING, MOMENT TENSORS, & SOURCE PARAMETERS Kikuchi and Kanamori, 1991

SOMETIMES FIRST MOTIONS DON’T CONSTRAIN FOCAL MECHANISM Especially likely when - Few nearby stations, as in the oceans, so arrivals are near center of focal sphere - Mechanism has significant dip-slip components, so planes don’t cross near center of focal sphere Additional information is obtained by comparing the observed body and surface waves to theoretical, or synthetic waveforms computed for various source parameters, and finding a model that best fits the data, either by forward modeling or inversion. Waveform analysis also gives information about earthquake depths and rupture processes that can’t be extracted from first motions. ? ? ?

SYNTHETIC SEISMOGRAM AS CONVOLUTION Regard ground motion recorded on seismogram as a combination of factors: - earthquake source - earth structure through which the waves propagated - seismometer Create synthetic seismogram as Fourier domain convolution of these effects

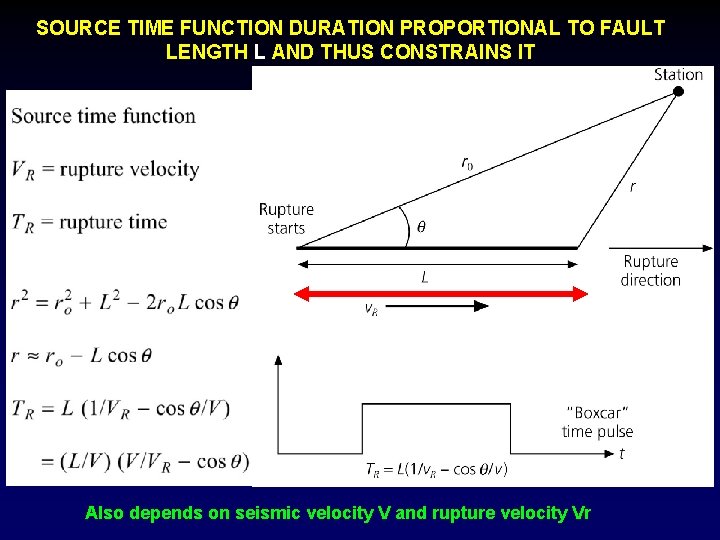
SOURCE TIME FUNCTION DURATION PROPORTIONAL TO FAULT LENGTH L AND THUS CONSTRAINS IT Also depends on seismic velocity V and rupture velocity Vr

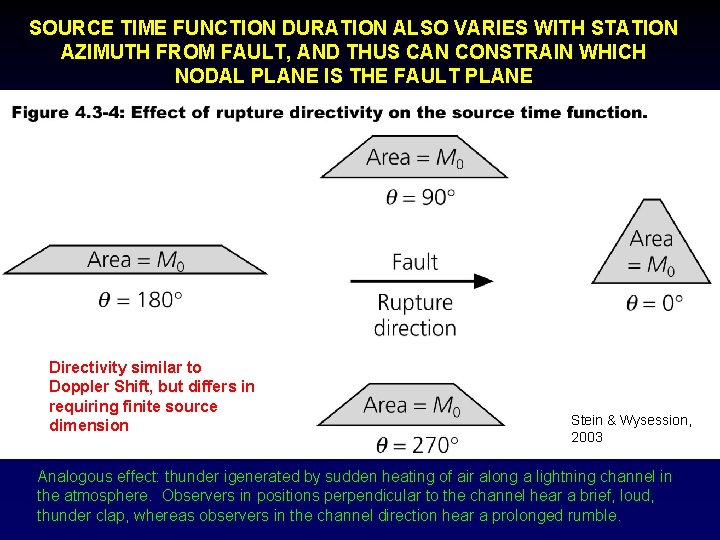
SOURCE TIME FUNCTION DURATION ALSO VARIES WITH STATION AZIMUTH FROM FAULT, AND THUS CAN CONSTRAIN WHICH NODAL PLANE IS THE FAULT PLANE Directivity similar to Doppler Shift, but differs in requiring finite source dimension Stein & Wysession, 2003 Analogous effect: thunder igenerated by sudden heating of air along a lightning channel in the atmosphere. Observers in positions perpendicular to the channel hear a brief, loud, thunder clap, whereas observers in the channel direction hear a prolonged rumble.

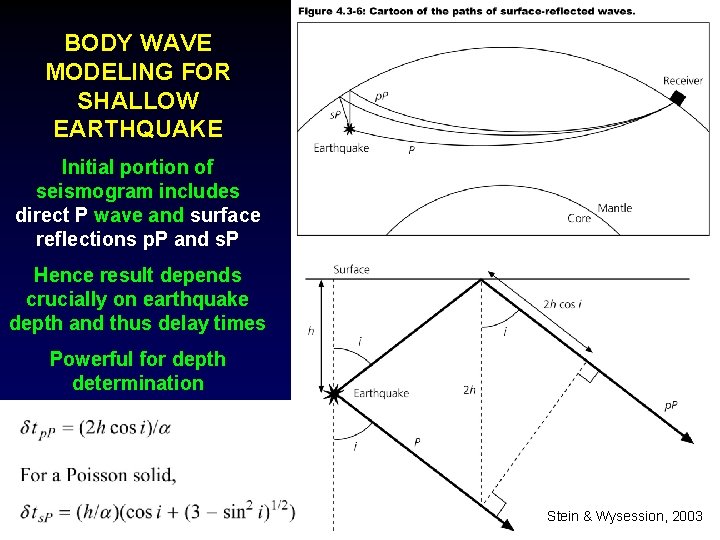
BODY WAVE MODELING FOR SHALLOW EARTHQUAKE Initial portion of seismogram includes direct P wave and surface reflections p. P and s. P Hence result depends crucially on earthquake depth and thus delay times Powerful for depth determination Stein & Wysession, 2003

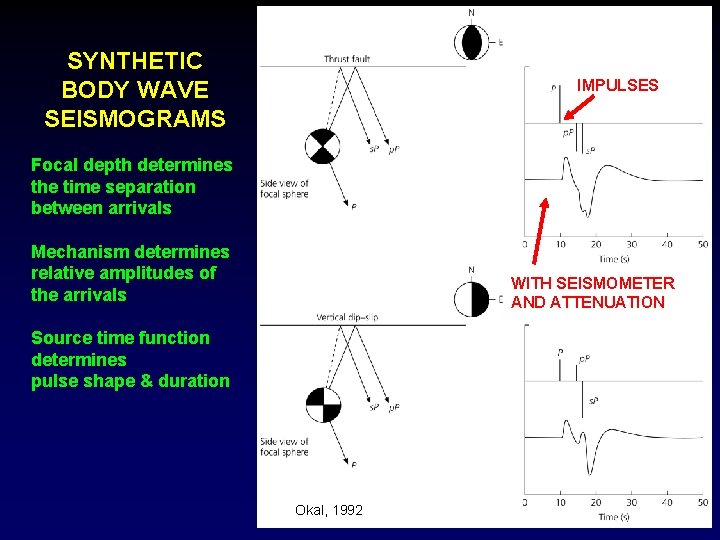
SYNTHETIC BODY WAVE SEISMOGRAMS IMPULSES Focal depth determines the time separation between arrivals Mechanism determines relative amplitudes of the arrivals WITH SEISMOMETER AND ATTENUATION Source time function determines pulse shape & duration Okal, 1992

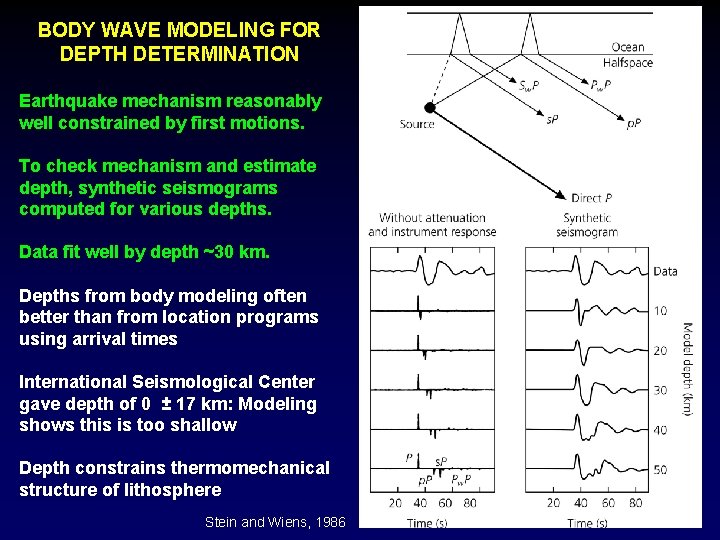
BODY WAVE MODELING FOR DEPTH DETERMINATION Earthquake mechanism reasonably well constrained by first motions. To check mechanism and estimate depth, synthetic seismograms computed for various depths. Data fit well by depth ~30 km. Depths from body modeling often better than from location programs using arrival times International Seismological Center gave depth of 0 ± 17 km: Modeling shows this is too shallow Depth constrains thermomechanical structure of lithosphere Stein and Wiens, 1986

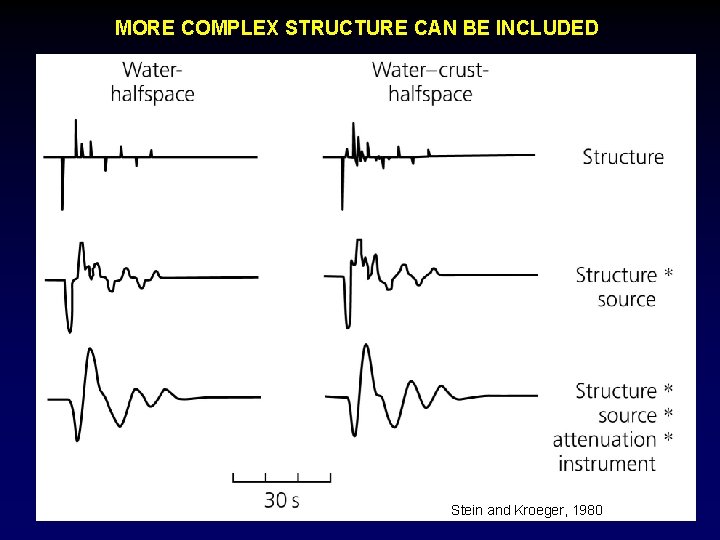
MORE COMPLEX STRUCTURE CAN BE INCLUDED Stein and Kroeger, 1980

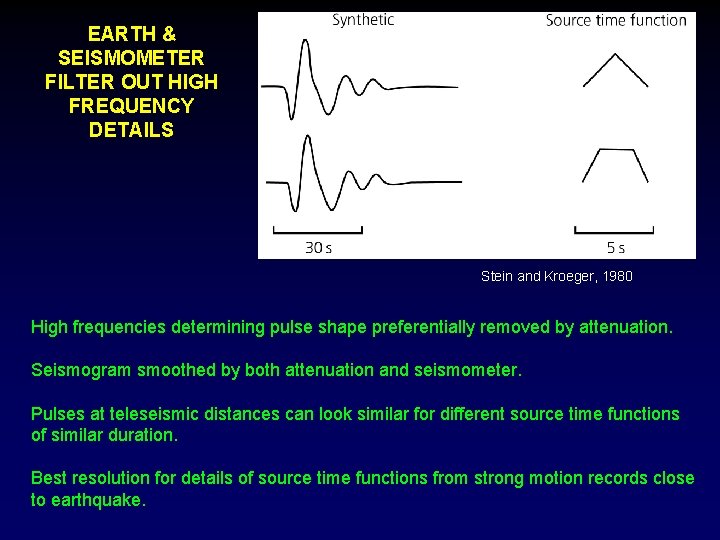
EARTH & SEISMOMETER FILTER OUT HIGH FREQUENCY DETAILS Stein and Kroeger, 1980 High frequencies determining pulse shape preferentially removed by attenuation. Seismogram smoothed by both attenuation and seismometer. Pulses at teleseismic distances can look similar for different source time functions of similar duration. Best resolution for details of source time functions from strong motion records close to earthquake.

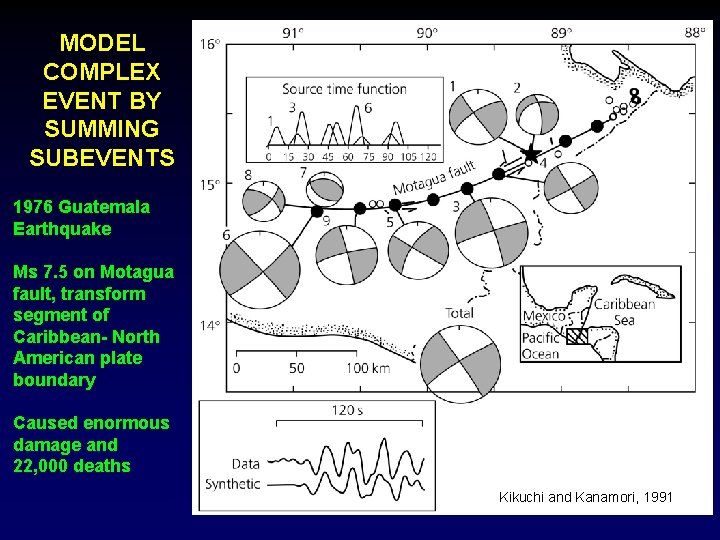
MODEL COMPLEX EVENT BY SUMMING SUBEVENTS 1976 Guatemala Earthquake Ms 7. 5 on Motagua fault, transform segment of Caribbean- North American plate boundary Caused enormous damage and 22, 000 deaths Kikuchi and Kanamori, 1991

SYNTHESIZE SURFACE WAVES IN FREQUENCY DOMAIN EARTH STRUCTURE SOURCE GEOMETRY

SURFACE WAVE AMPLITUDE RADIATION PATTERNS Amplitude radiation patterns for Love and Rayleigh waves corresponding to several focal mechanisms, all with a fault plane striking North. Show amplitude of surface waves in different directions Can be generated for any fault geometry and compared to observations to find the best fitting source geometry Stein & Wysession, 2003

SURFACE WAVE MECHANISM CONSTRAINT Normal faulting earthquake in diffuse plate boundary zone of Indian Ocean First motions constrain only E-W striking, north-dipping, nodal plane Second plane derived by matching theoretical surface wave amplitude radiation patterns (smooth line) to equalized data. Stein, 1978

SURFACE WAVE CONSTRAINT ON DEPTH How well waves of different periods are generated depends on depth DEPTH (km) Tsai & Aki, 1970

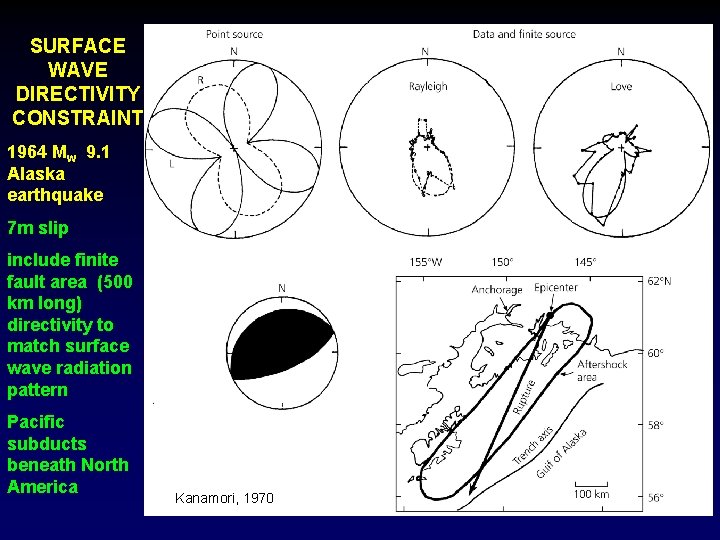
SURFACE WAVE DIRECTIVITY CONSTRAINT 1964 Mw 9. 1 Alaska earthquake 7 m slip include finite fault area (500 km long) directivity to match surface wave radiation pattern Pacific subducts beneath North America Kanamori, 1970

SEISMIC MOMENT TENSOR Represents other types of seismic sources as well as slip on a fault Gives additional insight into the rupture process Simplifies inverting (rather than forward modeling ) seismograms to estimate source parameters Used to produce global data set of great value for tectonics

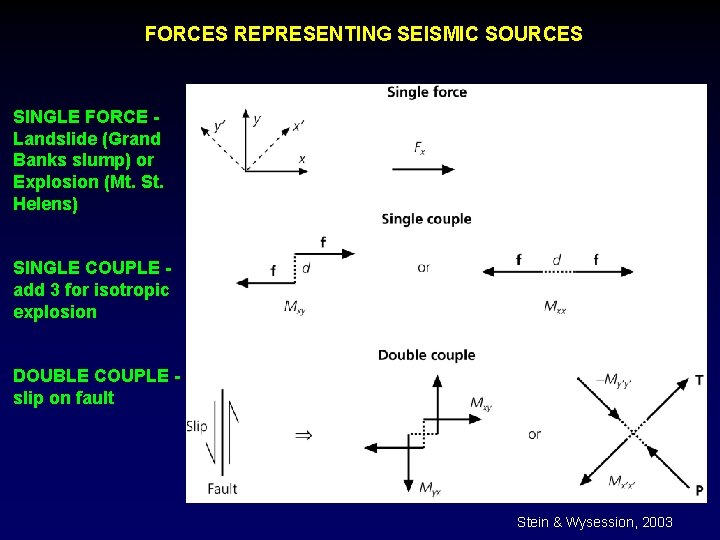
FORCES REPRESENTING SEISMIC SOURCES SINGLE FORCE Landslide (Grand Banks slump) or Explosion (Mt. St. Helens) SINGLE COUPLE add 3 for isotropic explosion DOUBLE COUPLE slip on fault Stein & Wysession, 2003

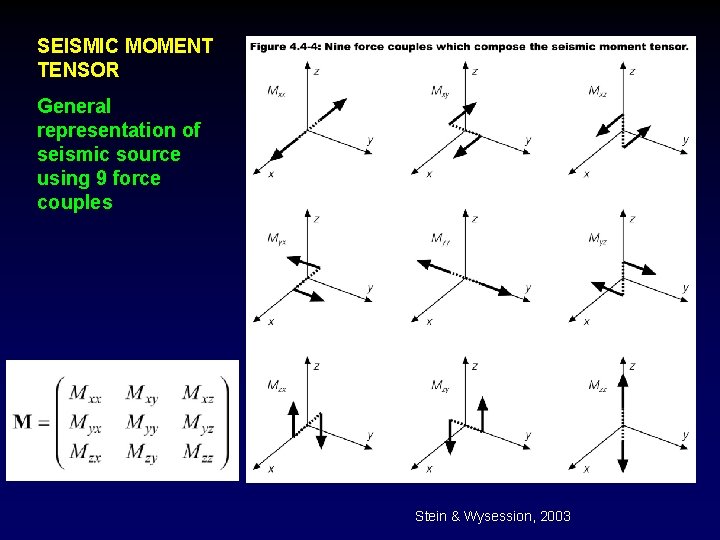
SEISMIC MOMENT TENSOR General representation of seismic source using 9 force couples Stein & Wysession, 2003

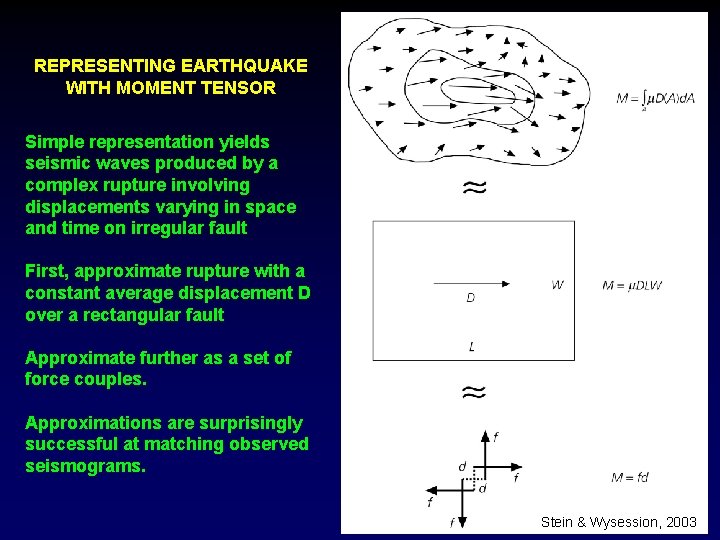
REPRESENTING EARTHQUAKE WITH MOMENT TENSOR Simple representation yields seismic waves produced by a complex rupture involving displacements varying in space and time on irregular fault First, approximate rupture with a constant average displacement D over a rectangular fault Approximate further as a set of force couples. Approximations are surprisingly successful at matching observed seismograms. Stein & Wysession, 2003

FOR FAULT ORIENTED NORMAL TO COORDINATE AXIS, MOMENT TENSOR IS Mo is scalar moment

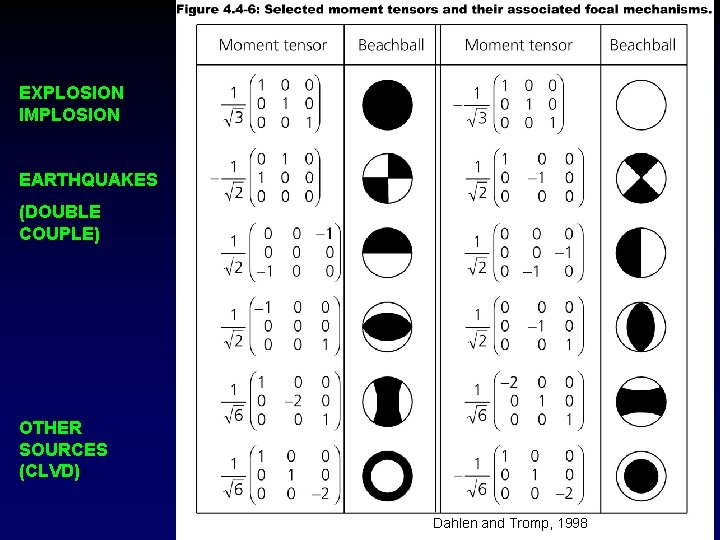
EXPLOSION IMPLOSION EARTHQUAKES (DOUBLE COUPLE) OTHER SOURCES (CLVD) Dahlen and Tromp, 1998

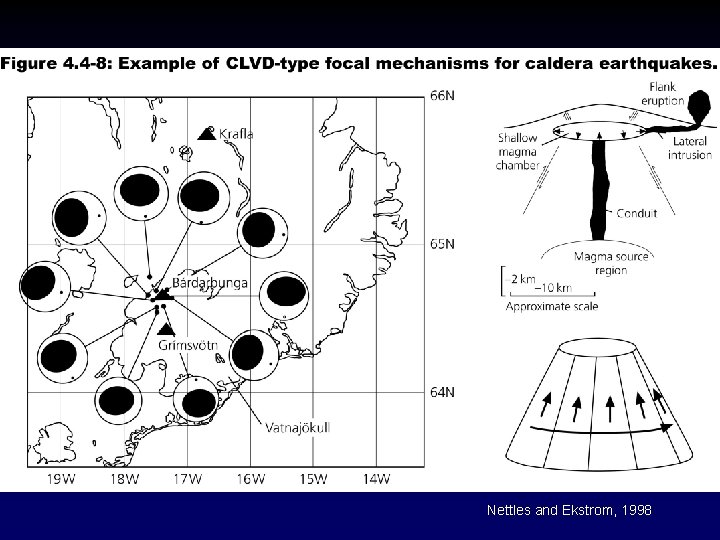
Nettles and Ekstrom, 1998

MOMENT TENSOR ADVANTAGES FOR SOURCE STUDIES: Analyze seismograms without assuming that they result from slip on a fault. In some applications, such as deep earthquakes or volcanic earthquakes, we would like to identify possible isotropic or CLVD components. Makes it easier to invert seismograms to find source parameters, because seismograms are linear functions of components of the moment tensor, but are complicated products of trigonometric functions of the fault strike, dip, and slip angles. This is not a problem in forward modeling, but makes it hard to invert the seismograms to find the fault angles.

MOMENT TENSOR DATA FOR TECTONIC STUDIES Globally-distributed broadband digital seismometers permit reliable focal mechanisms to be generated within minutes after most earthquakes with Ms > 5. 5 and made available through the Internet. Several organizations carry out this service, including the Harvard CMT (centroid moment tensor) project. CMT inversion yields both a moment tensor and a centroid time and location. This location often differs from that in earthquake bulletins, such as that of the International Seismological Centre (ISC), because the two locations tell different things. Bulletins based upon arrival times of body wave phases like P and S give the hypocenter: the point in space and time where rupture began. CMT solutions, using full waveforms, give the centroid or average location in space and time of the seismic energy release. The availability of large numbers of high-quality mechanisms (Harvard project has produced over 17, 000 solutions since 1976) is of great value in many applications, especially tectonic studies.

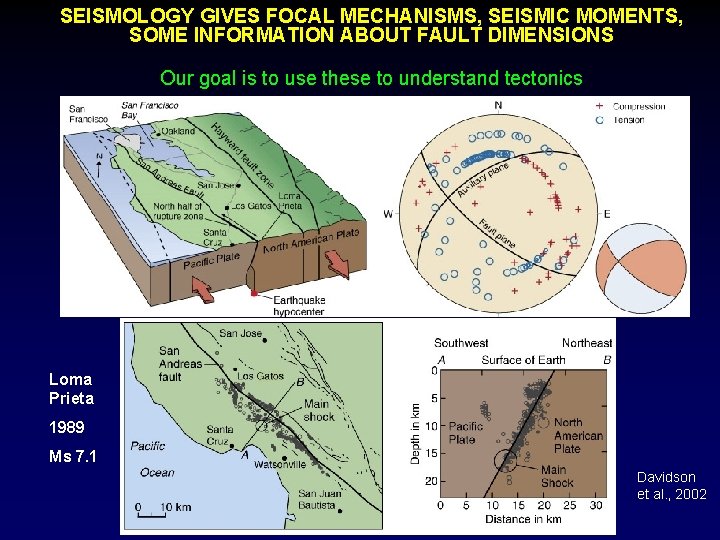
SEISMOLOGY GIVES FOCAL MECHANISMS, SEISMIC MOMENTS, SOME INFORMATION ABOUT FAULT DIMENSIONS Our goal is to use these to understand tectonics Loma Prieta 1989 Ms 7. 1 Davidson et al. , 2002

THREE EARTHQUAKES IN NORTH AMERICA PACIFIC PLATE BOUNDARY ZONE Tectonic setting affects earthquake size San Fernando earthquake on buried thrust fault in the Los Angeles area, similar to Northridge earthquake. Short faults are part of an oblique trend in the boundary zone, so fault areas are roughly rectangular. The down-dip width seems controlled by the fact that rocks deeper than ~20 km are weak and undergo stable sliding rather than accumulate strain for future earthquakes. San Francisco earthquake ruptured a long segment of the San Andreas with significantly larger slip, but because the fault is vertical, still had a narrow width. This earthquake illustrates approximately the maximum size of continental transform earthquakes. Stein & Wysession, 2003 Alaska earthquake had much larger rupture area because it occurred on shallow-dipping subduction thrust interface. The larger fault dimensions give rise to greater slip, so the combined effects of larger fault area and more slip cause largest earthquakes to occur at subduction zones rather than transforms.

EARTHQUAKE SOURCE PARAMETER ESTIMATES HAVE CONSIDERABLE UNCERTAINTIES FOR SEVERAL REASONS: - Uncertainties due to earth's variability and deviations from the mathematical simplifications used. Even with high-quality modern data, seismic moment estimates for the Loma Prieta earthquake vary by about 25%, and Ms values vary by about 0. 2 units. - Uncertainties for historic earthquakes are large. Fault length estimates for the San Francisco earthquake vary from 300 -500 km, Ms was estimated at 8. 3 but now thought to be ~7. 8, and fault width is essentially unknown and inferred from the depths of more recent earthquakes and geodetic data. - Different techniques (body waves, surface waves, geodesy, geology) can yield different estimates. - Fault dimensions and dislocations shown are average values for quantities that can vary significantly along the fault Hence different studies yield varying and sometimes inconsistent values. Even so, data are sufficient to show effects of interest.

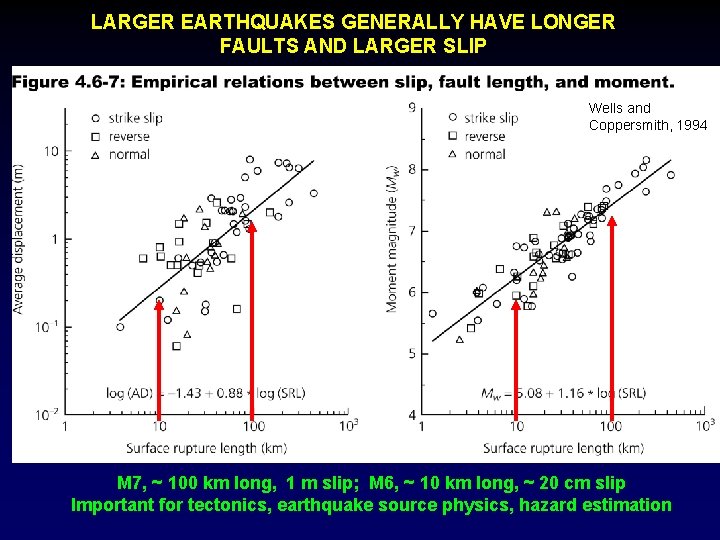
LARGER EARTHQUAKES GENERALLY HAVE LONGER FAULTS AND LARGER SLIP Wells and Coppersmith, 1994 M 7, ~ 100 km long, 1 m slip; M 6, ~ 10 km long, ~ 20 cm slip Important for tectonics, earthquake source physics, hazard estimation

IF STRESS DROP IN EARTHQUAKES IS APPROX IMATELY CONSTANT LONGER FAULTS (L LARGER) HAVE LARGER SLIP D

IF STRESS DROP IN EARTHQUAKES IS APPROX IMATELY CONSTANT LINEAR DIMENSION 3 OR FAULT AREA 3/2 INCREASES WITH MOMENT M 0

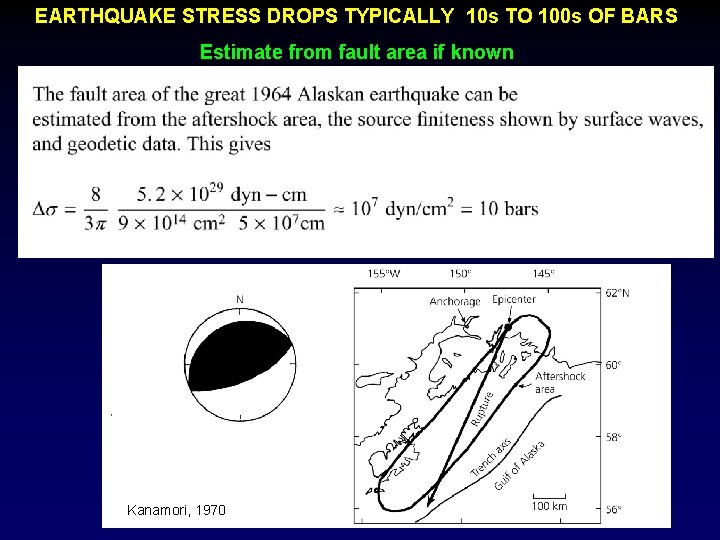
EARTHQUAKE STRESS DROPS TYPICALLY 10 s TO 100 s OF BARS Estimate from fault area if known Kanamori, 1970

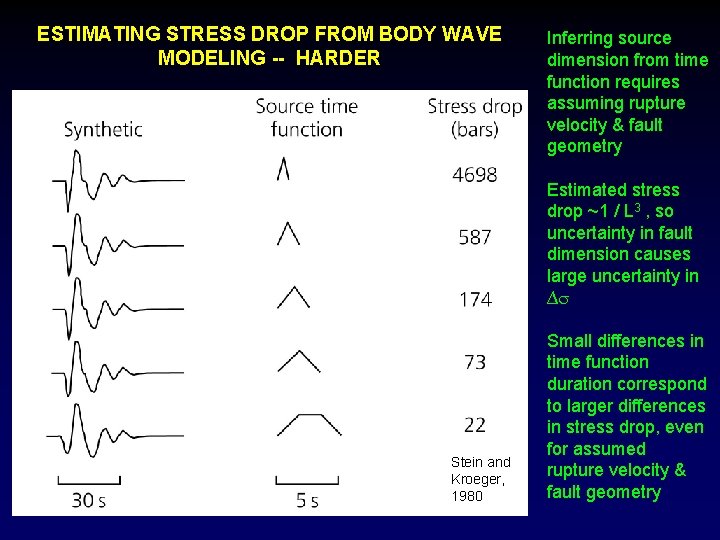
ESTIMATING STRESS DROP FROM BODY WAVE MODELING -- HARDER Inferring source dimension from time function requires assuming rupture velocity & fault geometry Estimated stress drop ~1 / L 3 , so uncertainty in fault dimension causes large uncertainty in ∆ Stein and Kroeger, 1980 Small differences in time function duration correspond to larger differences in stress drop, even for assumed rupture velocity & fault geometry

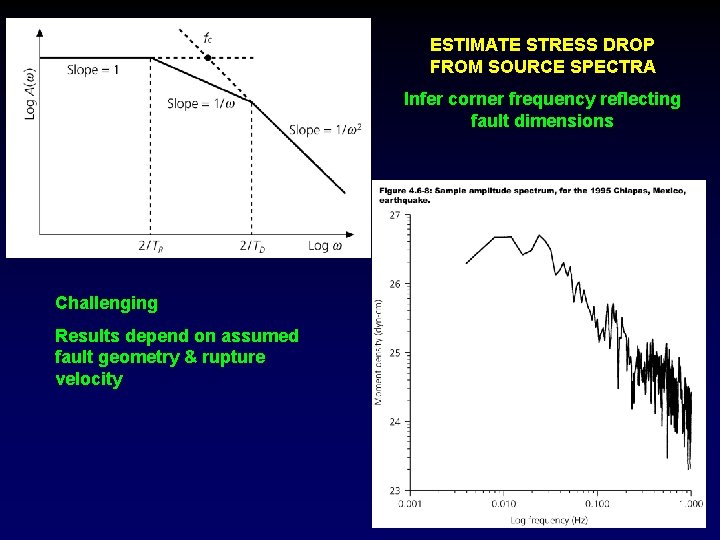
ESTIMATE STRESS DROP FROM SOURCE SPECTRA Infer corner frequency reflecting fault dimensions Challenging Results depend on assumed fault geometry & rupture velocity

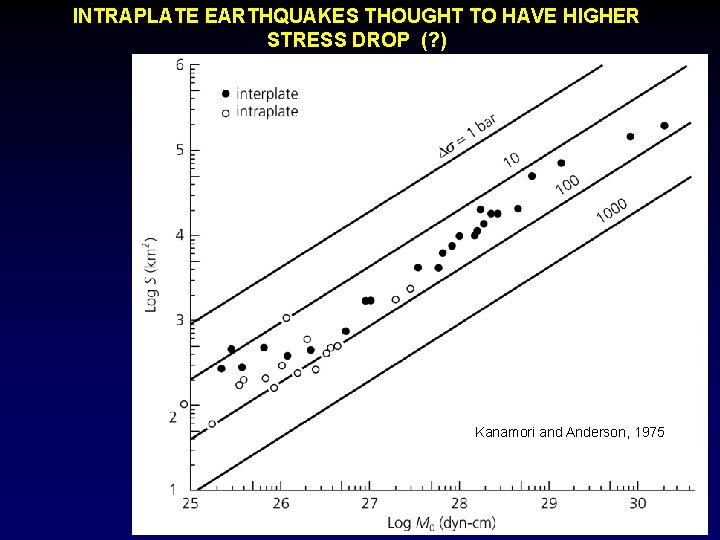
INTRAPLATE EARTHQUAKES THOUGHT TO HAVE HIGHER STRESS DROP (? ) Kanamori and Anderson, 1975

WHY? - Only a small fraction of stress released ? - Lab values apply to contact area, only a fraction of total fault surface ? -Lab values don’t scale correctly ?

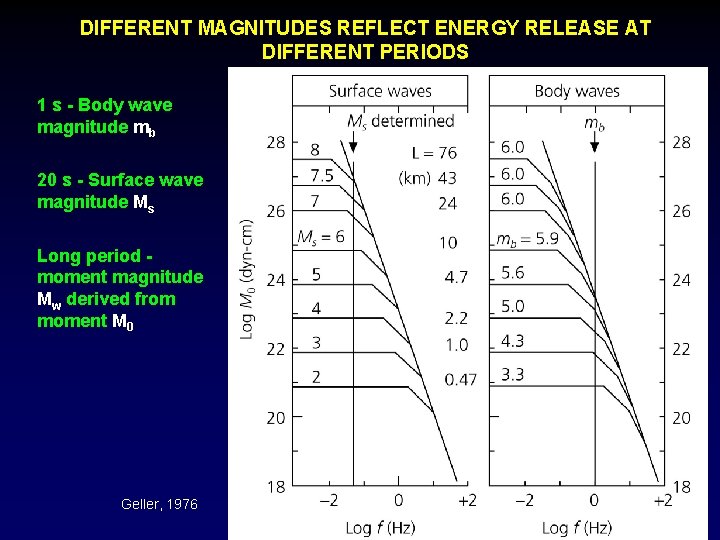
DIFFERENT MAGNITUDES REFLECT ENERGY RELEASE AT DIFFERENT PERIODS 1 s - Body wave magnitude mb 20 s - Surface wave magnitude Ms Long period moment magnitude Mw derived from moment M 0 Geller, 1976

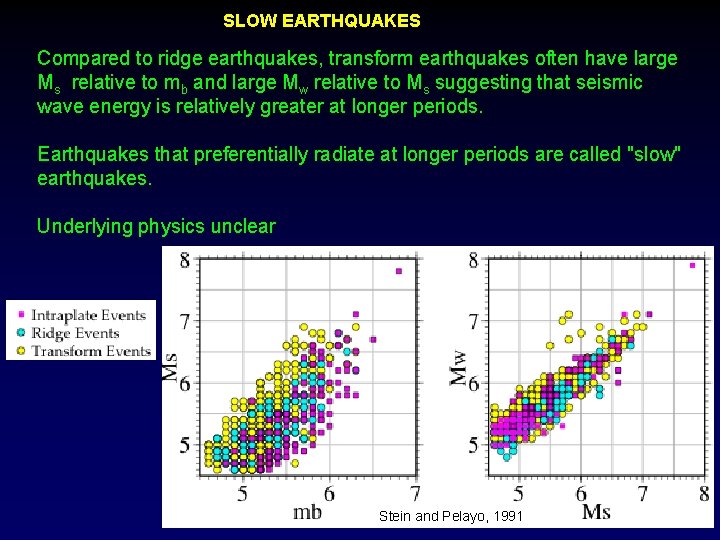
SLOW EARTHQUAKES Compared to ridge earthquakes, transform earthquakes often have large Ms relative to mb and large Mw relative to Ms suggesting that seismic wave energy is relatively greater at longer periods. Earthquakes that preferentially radiate at longer periods are called "slow" earthquakes. Underlying physics unclear Stein and Pelayo, 1991

ENERGY & MAGNITUDE 5

SUMMARY Body & surface waveform modeling improve estimates of focal mechanism & depth CMT data provides large mechanism dataset Some generalizations can be made about earthquake source parameters Results facilitate tectonic studies of plate motions, plate boundary zone and intraplate deformation, and thermomechanical structure of the lithosphere