Earth Science 3 Minerals and Mineral Deposits GEOL

Earth Science 3: Minerals and Mineral Deposits. GEOL 1103 Name: Donovan Blissett Ph. D (UNB), BSc (Hons; Mona) E-mail: donovan. blissett@gmail. com Office location: main bldg Consultation: 8 am-5 pm daily Important: Kindly purchase Lab Manual at the main office

Course Details Sign up sheets for tutorials and labs are in the office please sign up 3 tutorial assignments collect sheets with questions, date and hand in time to be announced 1 in-course test: week of February 13 Lab exam week of March 5

CRYSTALLOGRAPHY_1 January 2012 Acknowledgements: Modified from Prof. S. Nelson Tulane University

Mineralogy and Crystallography Introduction: What is a mineral? • a naturally occurring homogeneous solid • with a definite (but not generally fixed) chemical composition • a highly ordered atomic arrangement and • is usually formed by an inorganic process.

Naturally Occurring - synthetic minerals. Homogeneous - chemical compound. Definite chemical composition - chemical composition can be expressed by a chemical formula. Examples: Quartz: Si. O 2 ; Si and O in a ratio of 1 Si to 2 O atoms. Olivine: example of a mineral that does not have a fixed chemical composition. Mg and Fe atoms have the same size and charge and therefore can easily substitute for one another in a mineral. Thus, olivine can have the chemical formula Mg 2 Si. O 4 or Fe 2 Si. O 4 or anything in between. This is usually expressed with a formula indicating the possible substitution – (Mg, Fe)2 Si. O 4.

Highly ordered atomic arrangement - atoms in a mineral are arranged in an ordered geometric pattern. This ordered arrangement of atoms is called a crystal structure, and thus all minerals are crystals e. g. Diamond, Quartz. #36453, Diamond (5. 79 carat octahedral crystal), Mirny, Russia #43476, Quartz with Chalcopyrite, Deveti Septemvri Mine, Bulgaria http: //www. johnbetts-fineminerals. com/jhbnyc/oversize. htm

Note: A solid compound that meets the other criteria, but has no definite crystal structure is said to be amorphous. One of the consequences of this ordered internal arrangement of atoms is that all crystals of the same mineral look similar. Steno's Law of constancy of interfacial angles : (Nicolas Steno, 1669) Angles between corresponding crystal faces of the same mineral are identical. This is true even if the crystals are distorted as illustrated by the cross-sections through 3 quartz crystals shown below.

Crystal Construction Consider the basic units of crystals as cations surrounded by anions forming shapes called polyhedra. Anions form the corners of the polyhedra. Anions are generally much larger than the cations that fit between them. An important example of polyhedra is Si surrounded by 4 O in a tetrahedron.

Pauling (1929) established 5 rules. These rules describes cation-anion relationships in ionically bonded substances. Pauling’s rules 1: A polyhedron of anions is formed about each cation. The distance between a cation and an anion is determined by the sum of their radii (radius sum). The number of coordinated anions in the polyhedron is determined by the cation: anion radius ratio.

2 (electrostatic valency rule): States that an ionic structure is stable when the sum of the strengths of all the bonds that join the cation to the anions in the polyhedron balances (equals) the charge on the cation and the anions. 3: The sharing of edges and particularly faces by adjacent anion polyhedral elements decreases the stability of an ionic structure. Similar charges tends to repel. If they share components, adjacent polyhedra tend to share corners, rather than edges.

4: Cations with high valence charges and small Coordination number tend not to share polyhedral elements. Their positive charges tend to repel. 5 (rule of parsimony): The number of different cations and anions in a crystal structure tends to be small.

Coordination Number Coordination number (CN) = the number of ions surrounding (coordinating with) a cation or anion. CN is commonly 3, 4, 6, or 8 CN is less commonly 5, 7, 9, 10, 12 Clusters of atoms or ions bonded to other coordinating atoms produce Coordination Polyhedron structures.

Coordination Number Cations with CN=4 are said to be tetrahedrally coordinated or to reside in tetrahedral sites in a crystal structure. Cations with CN=6 are said to be octahedrally coordinated or to reside in octahedral sites in a crystal structure because they lie within 8 sided anion polyhedrons. Top view of octahedron CN=8 is called cubic coordination.

The no. of nearest neighbour anions that can be coordinated with a single cation depends on the radius ratio. Radius ratio RR=Rc/Ra Where Rc= radius of the smaller cation Ra=radius of the larger anion Eg. . Small highly charged cations coordinated with large highly charged anions The radius ratio (RR) and coordination no. is small. This is similar to fitting basketballs as spheres in contact around a marble. NOTE. Only two basketballs can fit as spheres around a small marble

Eg. . Small highly charged cations coordinated with small highly charged anions The radius ratio (RR) and coordination no. (CN) is larger. This is similar to fitting golf balls as spheres in contact around a large marble. NOTE. A large no. of golf balls can be fitted around a larger marble as spheres in contact because the radius ratio is larger. When prediction of CN using RR several factors must be taken into consideration. • The ionic radius and coordination number are not independent. As the effective ionic radius increases as coordination number increases.

• Since bonds are never truly ionic, models based on spheres in contact are only approximation. As bonds become more covalent and more highly polarized, radius ratios become increasing less effective in predicting coordination numbers. • Radius ratios do not successfully predict coordination number for metallically bonded substance.

Ionic Radius & Coordination Number Ionic radius is controlled by atomic number and charge and by coordination number. Anions are usually much larger than cations. Many cations are similar in size Si 4+ and Al 3+ Mg 2+, Fe 3+ Radius ratio between cation radius and anion radius acts as a control on CN especially when bonds are ionic. In general, higher radius ratio === higher CN lower radius ratio === lower CN

Radius ratio & coordination Cation/Anion In general larger radius ratio = higher CN Blue = Cation Red = Anion

Limiting ratio for octahedral coordination If anion diameter is considered to be 1 Then cation diameter = √ 2 – 1 Radius ratio = 0. 414

Electrostatic valency (EV) Another important concept related to the formation of coordination polyhedra is Electrostatic valency (EV). NOTE: the +ve on the cation is neutralised by the electrostatic component of the bonds between it and its nearest neighbour anions. For a cation of charge Z bonded to a number nearest neighbour anions, the EV of each bond is given by the charge of the cation divided by the number of nearest neighbours to which it is coordinated: EV=Z/CN

For EG. , the silica tetrahedron (Si. O 4)-4 each Si+4 cation is coordinated with four O-2 anions. Now EV= Z/CN = +4/4= +1

Meaning that each bond between the coordinating oxygen ions (O-2 ) balances a charge of +1. Or Each bond involves an electrostatic attraction between ions of opposite charge of one charge unit

Polymorphic Reactions Displacive polymorphic reactions- minor adjustment to the structure Order-disorder polymorphic reactions - moving from an ordered to disordered (or vice versa) arrangement of ions in sites within a crystal. (Microcline, Orthoclase, Sanidine KAl. Si 3 O 8) Reconstructive polymorphic reactions- breaking of atomic bonds. Common examples of reconstructive polymorphisms Graphite & Diamond– C (C has CN= 3 & 4 respectively) Calcite & Aragonite – Ca. CO 3 (Ca has CN=6 & 9 respectively)

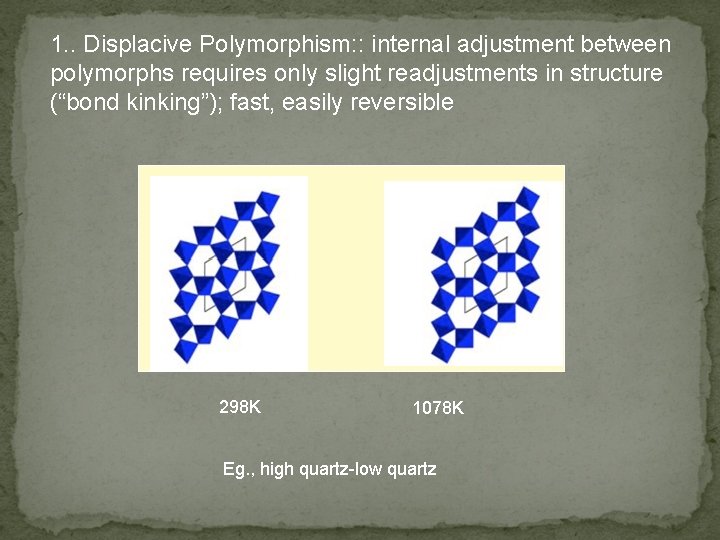
1. . Displacive Polymorphism: : internal adjustment between polymorphs requires only slight readjustments in structure (“bond kinking”); fast, easily reversible 298 K 1078 K Eg. , high quartz-low quartz

2. . Order--Disorder Polymorphism: : one polymorph has complete ordering, i. e. , atoms are all arranged in specific crystallographic locations, other polymorph has complete disorder, i. e. , atoms are randomly distributed over distinct structural sites High T => Less Ordered Low T => More Ordered structure: 100% probability of finding a given atom in a given site Disordered structure: a given site has a specific (e. g. 50%) probability of A and given probability (e. g. 50%) of finding B there Ex. . K-Feldspar (KAl. Si 3 O 8) All, , Si sites are interchangeable. . Sanidine: high T; random distribution of Al, Si over tetrahedral sites Microcline: : low T, , perfectly ordered distribution of Al, Si over T sites

3. Reconstructive Polymorphism: polymorphic reaction that requires bond breaking and reassembly of bonds; requires lots of energy; slow; difficult to reverse! Ex. Diamond – Graphite Also, Calcite - Aragonite

Solid Solution Solid solution is the substitution of one ion for another in a crystal lattice. This produces minerals with the same crystal structure but varying compositions. Ions with similar ionic radius and charge substitute for one another in a crystal structure.

Solid Solution and Ion Size If size difference between ions is <15% substitution likely, 15%-30% limited, >30% not likely. Common ions involved in substitutions- Fe 2+, Mg 2+ Na+, Ca 2+ Al 3+, Si 4+ Greater substitution possible at higher temperatures

Ionic Radii (in Å)

Example of Solid Solution Olivine – There is a complete solid solution between the minerals Forsterite (Mg 2 Si. O 4) & Fayalite (Fe 2 Si. O 4). The compositon of olivine is therefore (Mg, Fe)2 Si. O 4

Coupled Substitution If the substituting ions are of differing charge then more than one substitution must be made to balance the overall charge in the crystal (coupled substitution). Plagioclase feldspars A complete solid solution exists between Albite Na. Al. Si 3 O 8 & Anorthite Ca. Al 2 Si 2 O 8 Because Na and Ca have different charges (1+ and 2+) another substitution must be made, Al 3+ for Si 4+.

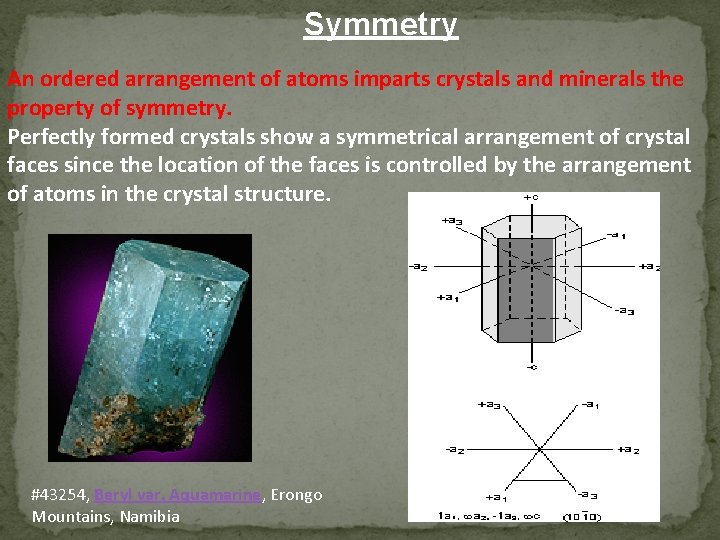
Symmetry An ordered arrangement of atoms imparts crystals and minerals the property of symmetry. Perfectly formed crystals show a symmetrical arrangement of crystal faces since the location of the faces is controlled by the arrangement of atoms in the crystal structure. #43254, Beryl var. Aquamarine, Erongo Mountains, Namibia

The atoms are arranged in a symmetrical fashion on a three dimensional network referred to as a Crystal lattice. When a crystal forms in an environment where there are no impediments to its growth, crystal faces form as smooth planar boundaries that make up the surface of the crystal. Crystal faces reflect the ordered internal arrangement of atoms and thus reflect the symmetry of the crystal lattice.

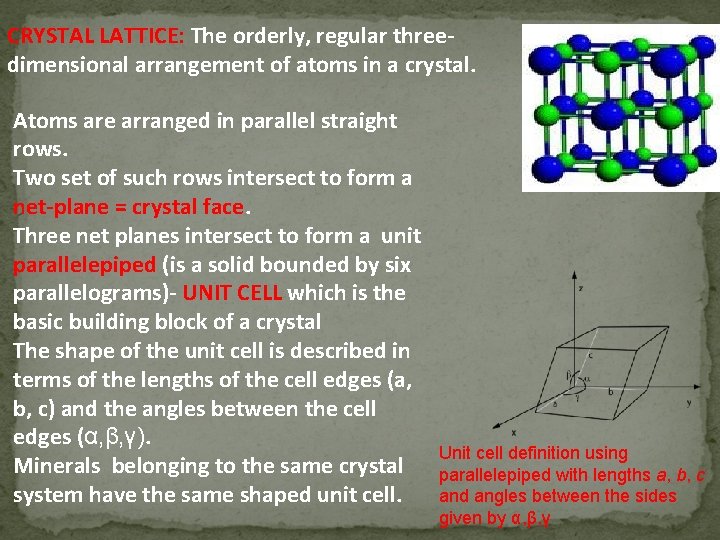
CRYSTAL LATTICE: The orderly, regular threedimensional arrangement of atoms in a crystal. Atoms are arranged in parallel straight rows. Two set of such rows intersect to form a net-plane = crystal face. Three net planes intersect to form a unit parallelepiped (is a solid bounded by six parallelograms)- UNIT CELL which is the basic building block of a crystal The shape of the unit cell is described in terms of the lengths of the cell edges (a, b, c) and the angles between the cell edges (α, β, γ). Minerals belonging to the same crystal system have the same shaped unit cell. Unit cell definition using parallelepiped with lengths a, b, c and angles between the sides given by α, β, γ

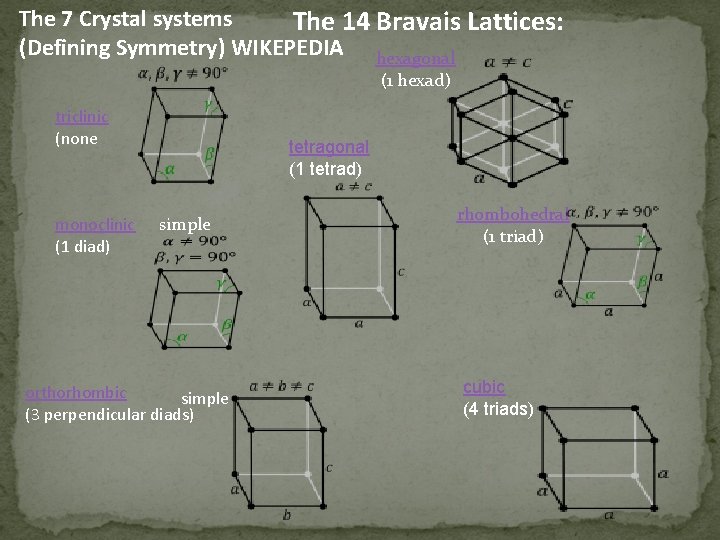
The 7 Crystal systems The 14 Bravais Lattices: (Defining Symmetry) WIKEPEDIA hexagonal (1 hexad) triclinic (none monoclinic (1 diad) tetragonal (1 tetrad) simple orthorhombic simple (3 perpendicular diads) rhombohedral (1 triad) cubic (4 triads)

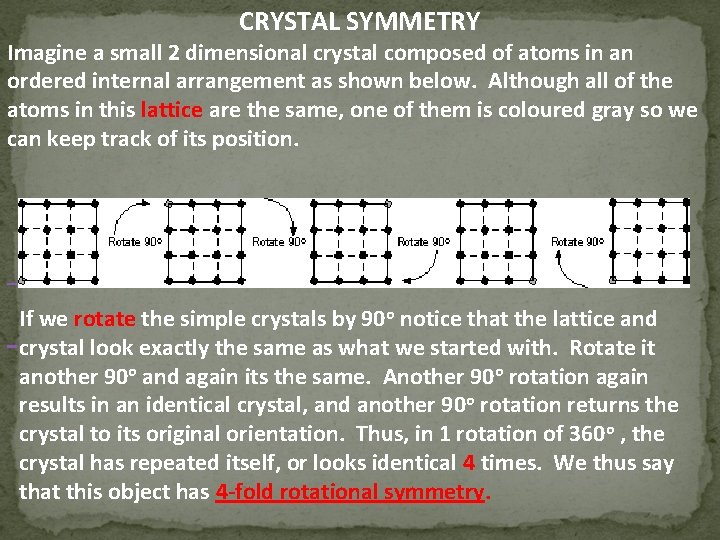
CRYSTAL SYMMETRY Imagine a small 2 dimensional crystal composed of atoms in an ordered internal arrangement as shown below. Although all of the atoms in this lattice are the same, one of them is coloured gray so we can keep track of its position. If we rotate the simple crystals by 90 o notice that the lattice and crystal look exactly the same as what we started with. Rotate it another 90 o and again its the same. Another 90 o rotation again results in an identical crystal, and another 90 o rotation returns the crystal to its original orientation. Thus, in 1 rotation of 360 o , the crystal has repeated itself, or looks identical 4 times. We thus say that this object has 4 -fold rotational symmetry.

Symmetry Operations and Elements A Symmetry operation is an operation that can be performed either physically or imaginatively and results in no change in the appearance of an object. Note: It is emphasized that in crystals, the symmetry is internal due to an ordered geometrical arrangement of atoms and molecules in the crystal lattice. Since the internal symmetry is reflected in the external form of perfect crystals, we are going to concentrate on external symmetry, using wooden models of crystals. There are 3 types of symmetry operations: rotation, reflection, and inversion.

Rotational Symmetry The imaginary axis along which the rotation is performed is an element of symmetry referred to as a rotation axis. Rotational symmetry axes possible in crystals are 1, 2, 3, 4, 6. 1 -Fold Rotation Axis - An object that requires rotation of a full 360 o in order to restore it to its original appearance has no rotational symmetry. Since it repeats itself 1 time every 360 o it is said to have a 1 -fold axis of rotational symmetry. 2 -fold Rotation Axis imagine rotation axis perpendicular to the page If an object appears identical after a rotation of 180 o, that is twice in a 360 o rotation, then it is said to have a 2 fold rotation axis (360/180 = 2). Note: A filled oval shape represents the point where the 2 fold rotation axis intersects the page.

3 -Fold Rotation Axis – An object that repeats itself after a rotation of 120 o is said to have a 3 fold axis of rotational symmetry, thus repeating itself 3 times in a 360 o rotation (360/120 =3). Note: A filled triangle is used to symbolize the location of 3 -fold rotation axis. 4 -Fold Rotation Axis - If an object repeats itself after 90 o of rotation, it will repeat 4 times in a 360 o rotation, as illustrated. Note: A filled square is used to symbolize the location of 4 -fold axis of rotational symmetry. 6 -Fold Rotation Axis - If rotation of 60 o about an axis causes the object to repeat itself, then it has 6 -fold axis of rotational symmetry (360/60=6). Note: A filled hexagon is used as the symbol for a 6 -fold rotation axis.

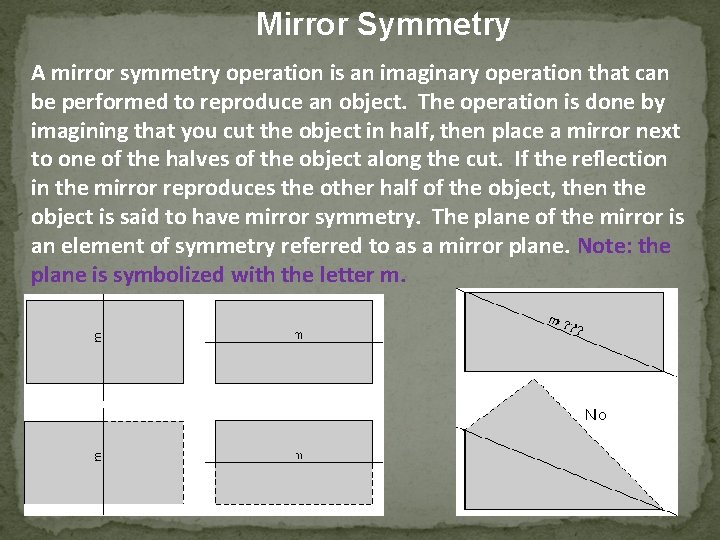
Mirror Symmetry A mirror symmetry operation is an imaginary operation that can be performed to reproduce an object. The operation is done by imagining that you cut the object in half, then place a mirror next to one of the halves of the object along the cut. If the reflection in the mirror reproduces the other half of the object, then the object is said to have mirror symmetry. The plane of the mirror is an element of symmetry referred to as a mirror plane. Note: the plane is symbolized with the letter m.

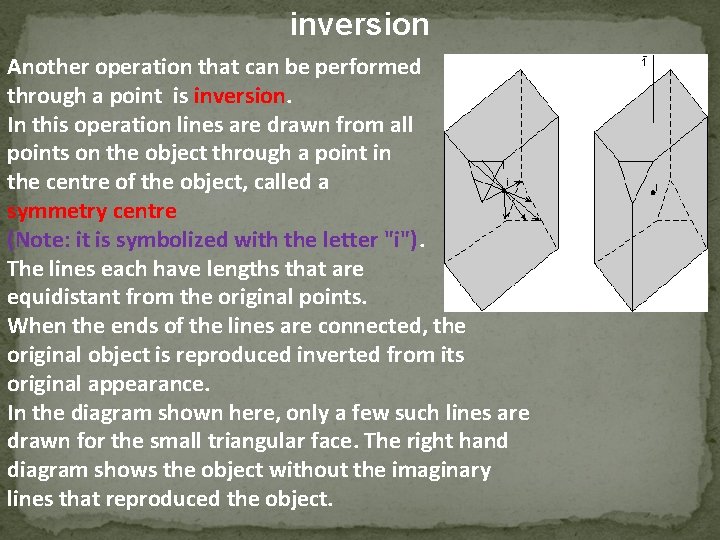
inversion Another operation that can be performed through a point is inversion. In this operation lines are drawn from all points on the object through a point in the centre of the object, called a symmetry centre (Note: it is symbolized with the letter "i"). The lines each have lengths that are equidistant from the original points. When the ends of the lines are connected, the original object is reproduced inverted from its original appearance. In the diagram shown here, only a few such lines are drawn for the small triangular face. The right hand diagram shows the object without the imaginary lines that reproduced the object.

If an object has only 1 centre of symmetry, we say that it has a 1 fold rotoinversion axis. Such an axis has the symbol (i), as shown in the right hand diagram above. Note that crystals that have a centre of symmetry will exhibit the property that if you place it on a table there will be a face on the top of the crystal that will be parallel to the surface of the table and identical to the face resting on the table. Rotoinversion Combinations of rotation with a centre of symmetry perform the symmetry operation of rotoinversion. Objects that have rotoinversion symmetry have an element of symmetry called a rotoinversion axis. A 1 fold rotoinversion axis is the same as a centre of symmetry, as discussed above.

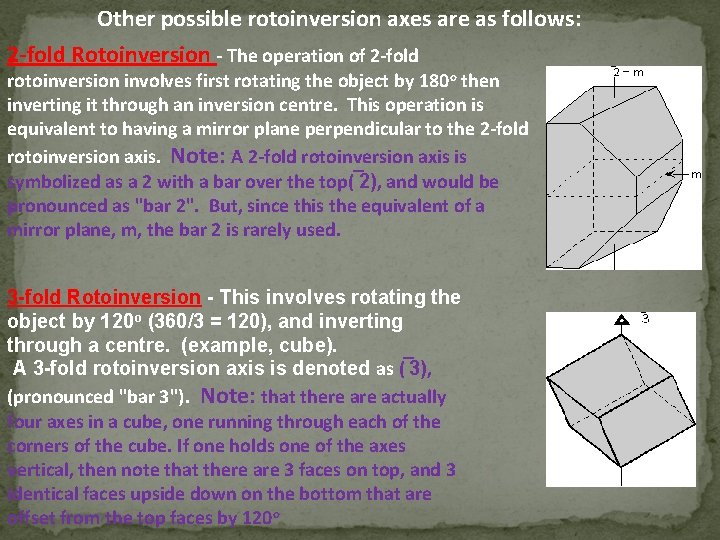
Other possible rotoinversion axes are as follows: 2 -fold Rotoinversion - The operation of 2 -fold rotoinversion involves first rotating the object by 180 o then inverting it through an inversion centre. This operation is equivalent to having a mirror plane perpendicular to the 2 -fold rotoinversion axis. Note: A 2 -fold rotoinversion axis is symbolized as a 2 with a bar over the top( 2), and would be pronounced as "bar 2". But, since this the equivalent of a mirror plane, m, the bar 2 is rarely used. 3 -fold Rotoinversion - This involves rotating the object by 120 o (360/3 = 120), and inverting through a centre. (example, cube). A 3 -fold rotoinversion axis is denoted as ( 3), (pronounced "bar 3"). Note: that there actually four axes in a cube, one running through each of the corners of the cube. If one holds one of the axes vertical, then note that there are 3 faces on top, and 3 identical faces upside down on the bottom that are offset from the top faces by 120 o

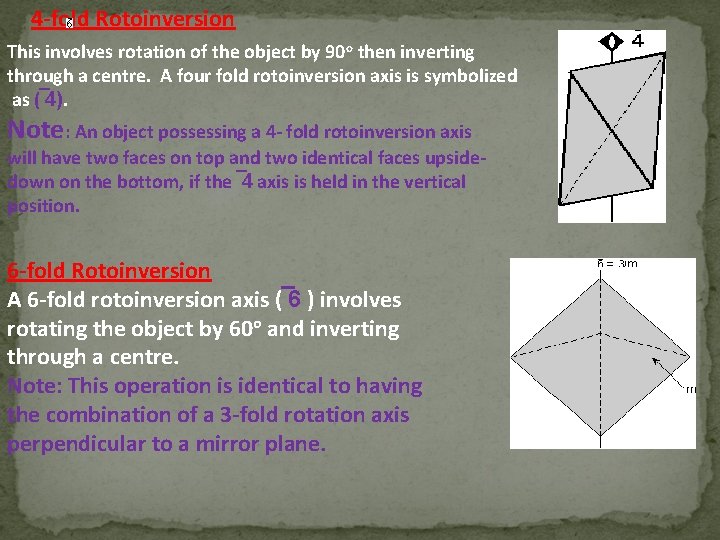
4 -fold Rotoinversion This involves rotation of the object by 90 o then inverting through a centre. A four fold rotoinversion axis is symbolized as ( 4). Note: An object possessing a 4 - fold rotoinversion axis will have two faces on top and two identical faces upsidedown on the bottom, if the 4 axis is held in the vertical position. 6 -fold Rotoinversion A 6 -fold rotoinversion axis ( 6 ) involves rotating the object by 60 o and inverting through a centre. Note: This operation is identical to having the combination of a 3 -fold rotation axis perpendicular to a mirror plane.

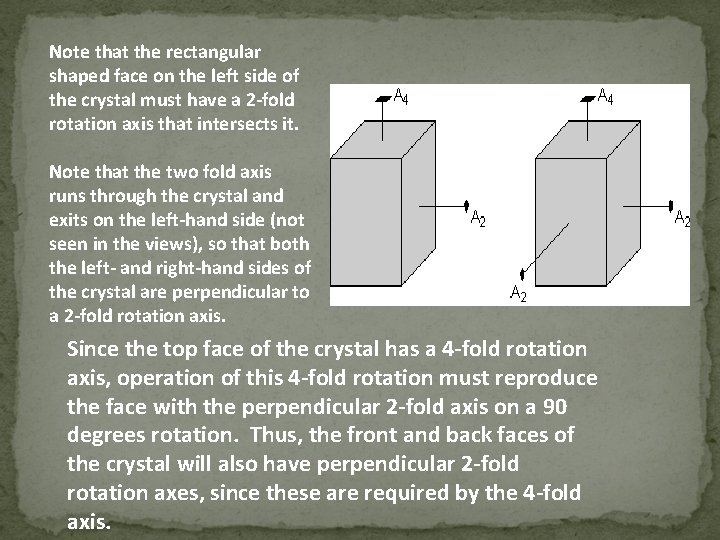
Combinations of Symmetry Operations In crystals there are ONLY 32 possible combinations of symmetry elements. These 32 combinations define the 32 Crystal Classes. Every crystal must belong to one of these 32 crystal classes. Example of how the various symmetry elements are combined in a somewhat completed crystal. If 2 kinds of symmetry elements are present in the same crystal, then they will operate on each other to produce other symmetrical symmetry elements. The crystal shown has rectangular-shaped sides with a square- shaped top and bottom. The square-shaped top indicates that there must be a 4 -fold rotation axis perpendicular to the square shaped face.

Note that the rectangular shaped face on the left side of the crystal must have a 2 -fold rotation axis that intersects it. Note that the two fold axis runs through the crystal and exits on the left-hand side (not seen in the views), so that both the left- and right-hand sides of the crystal are perpendicular to a 2 -fold rotation axis. Since the top face of the crystal has a 4 -fold rotation axis, operation of this 4 -fold rotation must reproduce the face with the perpendicular 2 -fold axis on a 90 degrees rotation. Thus, the front and back faces of the crystal will also have perpendicular 2 -fold rotation axes, since these are required by the 4 -fold axis.

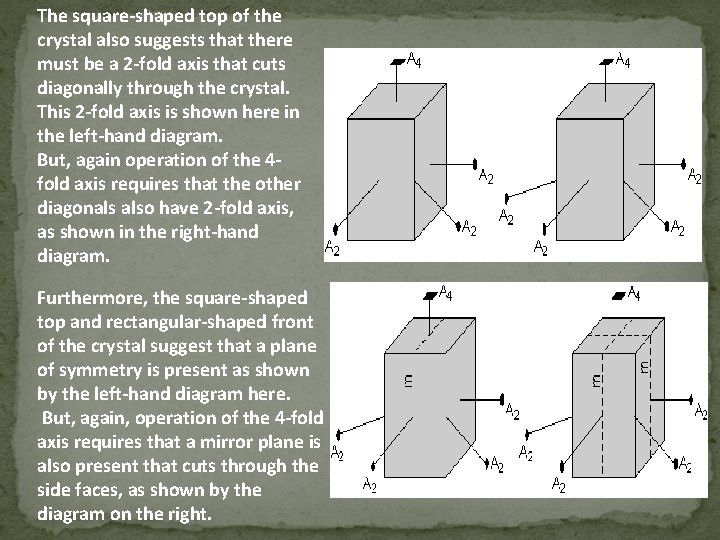
The square-shaped top of the crystal also suggests that there must be a 2 -fold axis that cuts diagonally through the crystal. This 2 -fold axis is shown here in the left-hand diagram. But, again operation of the 4 fold axis requires that the other diagonals also have 2 -fold axis, as shown in the right-hand diagram. Furthermore, the square-shaped top and rectangular-shaped front of the crystal suggest that a plane of symmetry is present as shown by the left-hand diagram here. But, again, operation of the 4 -fold axis requires that a mirror plane is also present that cuts through the side faces, as shown by the diagram on the right.

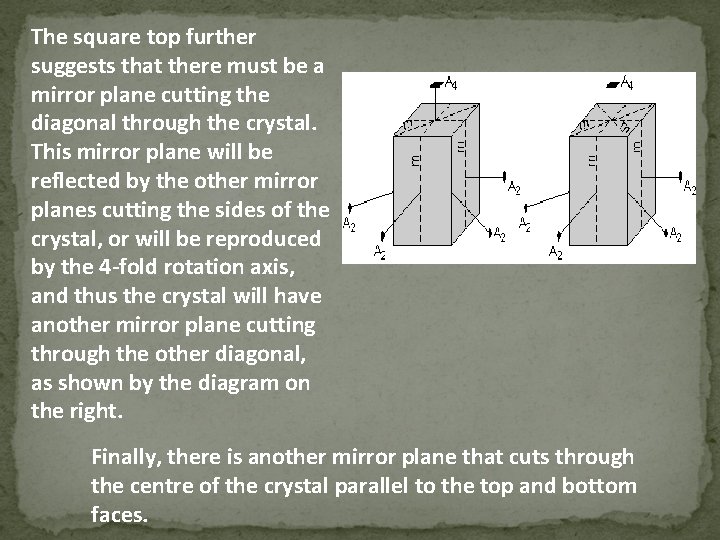
The square top further suggests that there must be a mirror plane cutting the diagonal through the crystal. This mirror plane will be reflected by the other mirror planes cutting the sides of the crystal, or will be reproduced by the 4 -fold rotation axis, and thus the crystal will have another mirror plane cutting through the other diagonal, as shown by the diagram on the right. Finally, there is another mirror plane that cuts through the centre of the crystal parallel to the top and bottom faces.

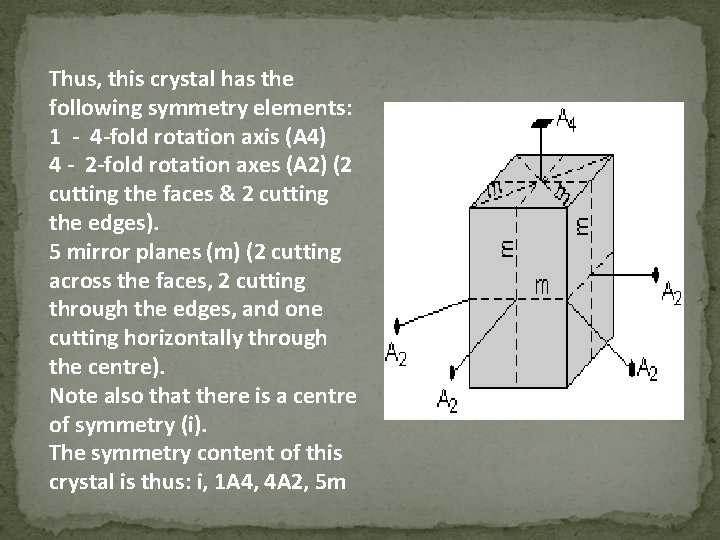
Thus, this crystal has the following symmetry elements: 1 - 4 -fold rotation axis (A 4) 4 - 2 -fold rotation axes (A 2) (2 cutting the faces & 2 cutting the edges). 5 mirror planes (m) (2 cutting across the faces, 2 cutting through the edges, and one cutting horizontally through the centre). Note also that there is a centre of symmetry (i). The symmetry content of this crystal is thus: i, 1 A 4, 4 A 2, 5 m

External Symmetry of Crystals, 32 Crystal Classes Hermann- Mauguin (International) Symbols How to derive the Hermann- Mauguin symbols (also called the international symbols) used to describe the crystal classes from the symmetry content. We'll start with a simple crystal then look at some more complex examples. The rectangular block shown here has 3 2 -fold rotation axes (A 2), 3 mirror planes (m), and a centre of symmetry (i) (3 A 2, 3 m, i). Rule for the derivation of the Hermann-Mauguin symbol are as follows: Write a number representing each of the unique rotation axes present (A unique rotation axis is one that exists by itself and is not produced by another symmetry operation). Eg. 1 - In this case, all three 2 -fold axes are unique, because each is perpendicular to a different shaped face, so we write a 2 (for 2 -fold) for each axis 2 2 2

Next we write an "m" for each unique mirror plane. (A unique mirror plane is one that is not produced by any other symmetry operation). In this example, we can tell that each mirror is unique because each one cuts a different face. So, we write: 2 m 2 m If any of the axes are perpendicular to a mirror plane we put a slash (/) between the symbol for the axis and the symbol for the mirror plane. In this case, each of the 2 -fold axes are perpendicular to mirror planes, so our symbol becomes: 2/m 2/m

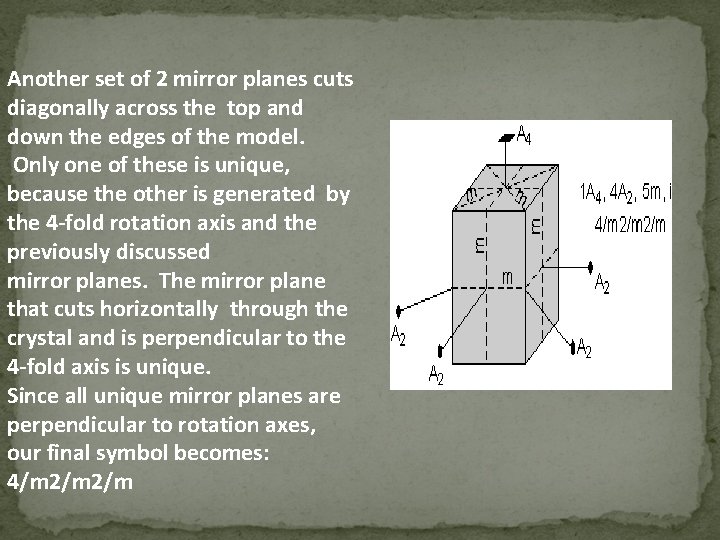
Eg. 2. Contains 1 4 -fold axis, 4 2 -fold axes, 5 mirror planes, and a centre of symmetry (1 A 4, 4 A 2, 5 m, i). Note that the 4 -fold axis is unique. There are 2 2 -fold axes that are perpendicular to identical faces, and 2 2 -fold axes that run through the vertical edges of the crystal. Thus there are only 2 unique 2 fold axes, because the others are required by the 4 -fold axis perpendicular to the top face. So, we write: 4 2 2 Although there are 5 mirror planes in the model, only 3 of them are unique. Two mirror planes cut the front and side faces of the crystal, and are perpendicular to the 2 -fold axes that are perpendicular to these faces. Only one of these is unique, because the other is required by the 4 -fold rotation axis.

Another set of 2 mirror planes cuts diagonally across the top and down the edges of the model. Only one of these is unique, because the other is generated by the 4 -fold rotation axis and the previously discussed mirror planes. The mirror plane that cuts horizontally through the crystal and is perpendicular to the 4 -fold axis is unique. Since all unique mirror planes are perpendicular to rotation axes, our final symbol becomes: 4/m 2/m

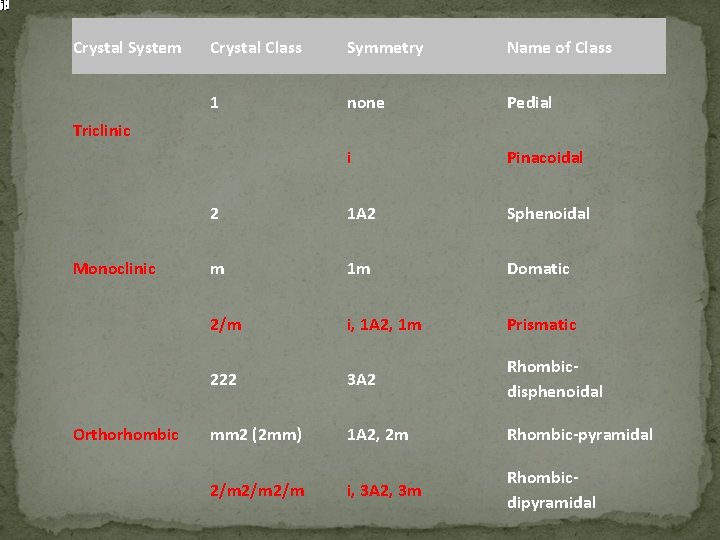
Crystal System Crystal Class Symmetry Name of Class 1 none Pedial i Pinacoidal 2 1 A 2 Sphenoidal m 1 m Domatic 2/m i, 1 A 2, 1 m Prismatic 222 3 A 2 Rhombicdisphenoidal mm 2 (2 mm) 1 A 2, 2 m Rhombic-pyramidal 2/m 2/m i, 3 A 2, 3 m Rhombicdipyramidal Triclinic Monoclinic Orthorhombic

4 1 A 4 4 Tetragonal 4/m i, 1 A 4, 1 m 422 1 A 4, 4 A 2 4 mm 1 A 4, 4 m 2 m 1 4, 2 A 2, 2 m 4/m 2/m i, 1 A 4, 4 A 2, 5 m 3 1 A 3 1 3 32 1 A 3, 3 A 2 3 m 1 A 3, 3 m Tetragonal- Pyramidal Tetragonaldisphenoidal Tetragonaldipyramidal Tetragonaltrapezohedral Ditetragonalpyramidal Tetragonalscalenohedral Ditetragonaldipyramidal Trigonal-pyramidal Rhombohedral Trigonaltrapezohedral Ditrigonal-pyramidal

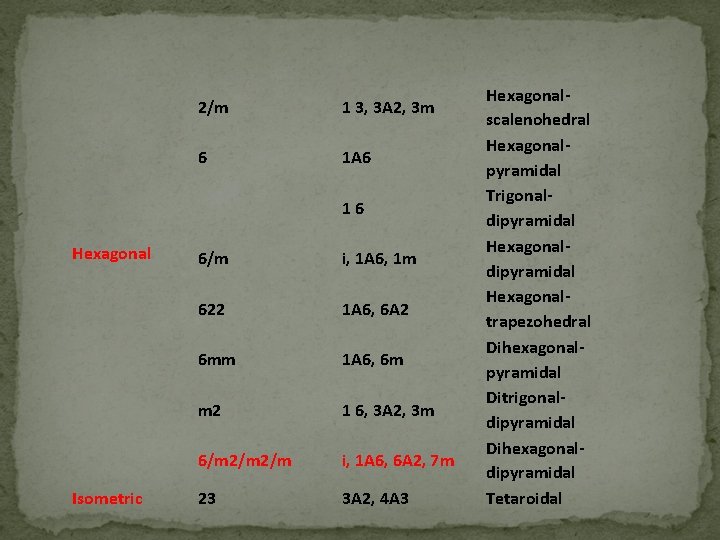
2/m 1 3, 3 A 2, 3 m 6 1 A 6 1 6 Hexagonal Isometric 6/m i, 1 A 6, 1 m 622 1 A 6, 6 A 2 6 mm 1 A 6, 6 m m 2 1 6, 3 A 2, 3 m 6/m 2/m i, 1 A 6, 6 A 2, 7 m 23 3 A 2, 4 A 3 Hexagonalscalenohedral Hexagonalpyramidal Trigonaldipyramidal Hexagonaltrapezohedral Dihexagonalpyramidal Ditrigonaldipyramidal Dihexagonaldipyramidal Tetaroidal

Isometric 2/m 432 3 m 4/m bar 3 2/m 3 A 2, 3 m, 4 3 3 A 4, 4 A 3, 6 A 2 3 4, 4 A 3, 6 m 3 A 4, 4 3, 6 A 2, 9 m Diploidal Gyroidal Hextetrahedral Hexoctahedral

32 crystal classes are divided into 6 crystal systems DIAGNOSTIC SYMMETRY Triclinic System: 1 -fold or 1 -fold rotoinversion axes/ centre Monoclinic System: mirror plane or a single 2 -fold axis Orthorhombic System: three 2 -fold axes /or 3 mirror planes Tetragonal System : single 4 -fold axis Hexagonal System : one 6 -fold or 3 -fold axis Isometric System: four 3 -fold axes

Next lecture will begin with the description of all the crystal classes