EART 20170 Computing Data Analysis Communication skills Lecturer

EART 20170 Computing, Data Analysis & Communication skills Lecturer: Dr Paul Connolly (F 18 – Sackville Building) p. connolly@manchester. ac. uk 1. Data analysis (statistics) 3 lectures & practicals statistics open-book test (2 hours) 2. Computing (Excel statistics/modelling) 2 lectures assessed practical work Course notes etc: http: //cloudbase. phy. umist. ac. uk/people/connolly Recommended reading: Cheeney. (1983) Statistical methods in Geology. George, Allen & Unwin

Recap – last lecture n The four measurement scales: nominal, ordinal, interval and ratio. n There are two types of errors: random errors (precision) and systematic errors (accuracy). n Basic graphs: histograms, frequency polygons, bar charts, pie charts. n Gaussian statistics describe random errors. n The central limit theorem n Central values, dispersion, symmetry n Weighted mean.

Some common problems

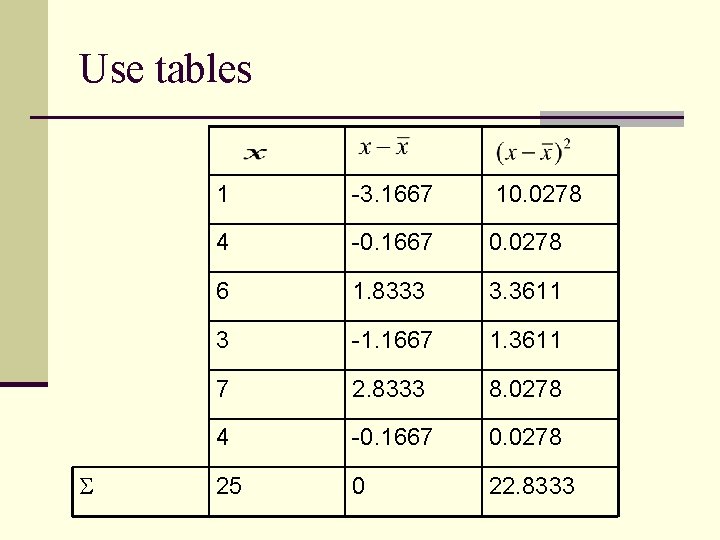
Use tables 1 -3. 1667 10. 0278 4 -0. 1667 0. 0278 6 1. 8333 3. 3611 3 -1. 1667 1. 3611 7 2. 8333 8. 0278 4 -0. 1667 0. 0278 25 0 22. 8333

Lecture 2 n Correlation between two variables n Classical linear regression n Reduced major axis regression n Propagation of errors in compound quantities.

Correlation n Many real-life quantities have a dependence on some thing else. E. g dependence of rock permeability on porosity. n How can we quantify the strength and direction of a linear relationship between X and Y variables?

Correlation n Linear correlation (Pearson’s coefficient) n n n y = sum of all y-values x = sum of all x-values x 2 = sum of all x 2 values y 2 = sum of all y 2 values xy = sum of the x times y values n Like other numerical measures, the population correlation coefficient is (the Greek letter ``rho'‘, ) and the sample correlation coefficient is denoted by r.

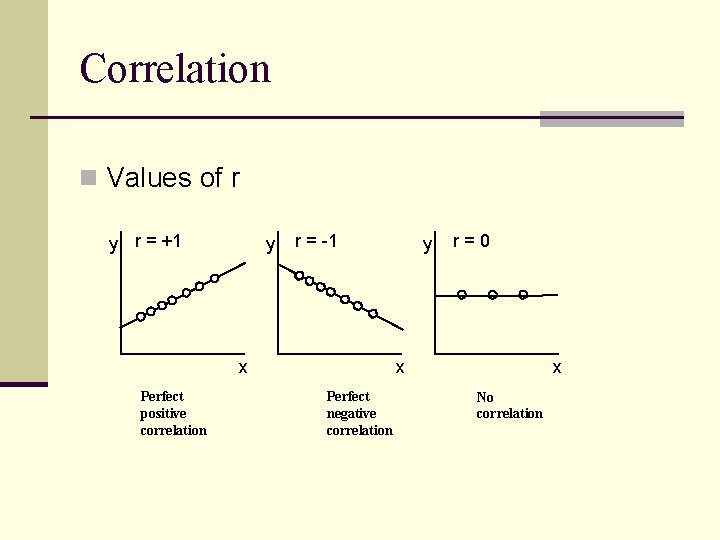
Correlation n Values of r y r = +1 y r = -1 x Perfect positive correlation y r=0 x Perfect negative correlation x No correlation

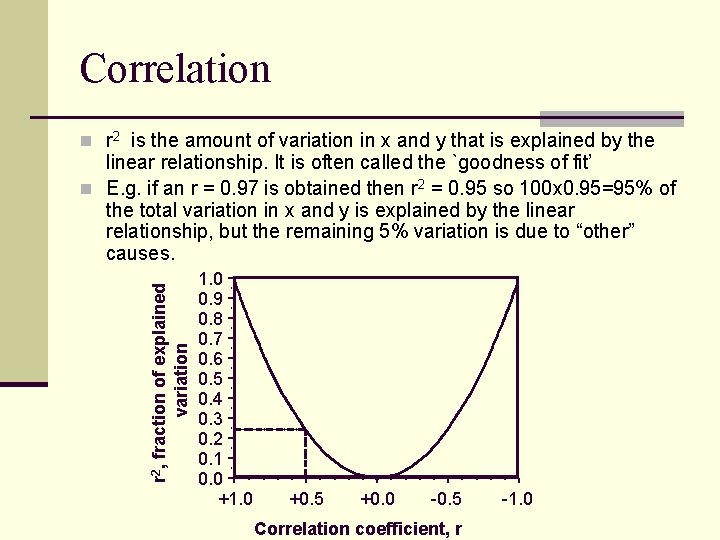
Correlation n r 2 is the amount of variation in x and y that is explained by the r 2, fraction of explained variation linear relationship. It is often called the `goodness of fit’ n E. g. if an r = 0. 97 is obtained then r 2 = 0. 95 so 100 x 0. 95=95% of the total variation in x and y is explained by the linear relationship, but the remaining 5% variation is due to “other” causes. 1. 0 0. 9 0. 8 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 0. 0 +1. 0 +0. 5 +0. 0 -0. 5 Correlation coefficient, r -1. 0

Regression analysis n How can we fit an equation to a set of numerical data x, y such that it yields the best fit for all the data?

Classical linear regression n An approximate fit yields a straight line that passes through the set of points in the best possible manner without being required to pass exactly through any of the points.

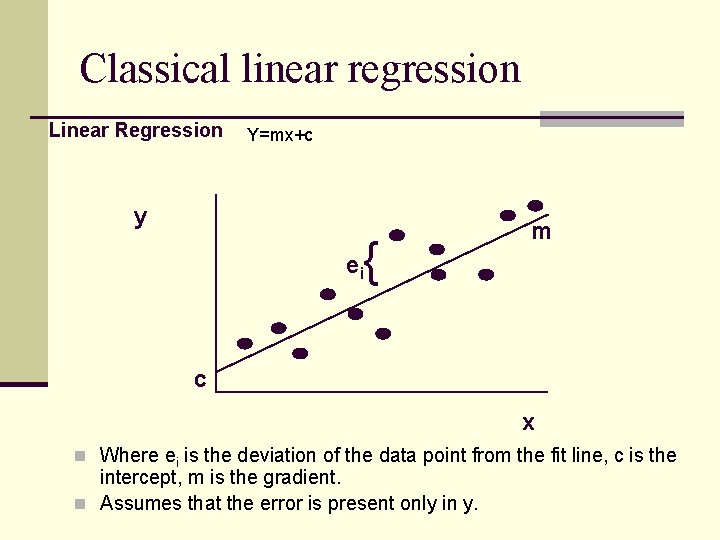
Classical linear regression Linear Regression Y=mx+c y { m ei c x n Where ei is the deviation of the data point from the fit line, c is the intercept, m is the gradient. n Assumes that the error is present only in y.

How do we define a good fit? n If the sum of all deviations is a minimum? ei n If the sum of all the absolute deviations is a minimum? |ei| n If the maximum deviation is a minimum? emax n If the sum of all the squares of the deviations is a minimum? ei 2

Classical linear regression n The best way is to minimise the sum of the squares of the deviation. Formally this involves some Mathematics: n At each value of xi: n Therefore the deviations from the curve are: n The sum of the squares:

Classical linear regression n How do you find the minimum of a function? n Use calculus n Differentiate and set to zero n Two simultaneous equations

Classical linear regression n Solving the two equations yields:

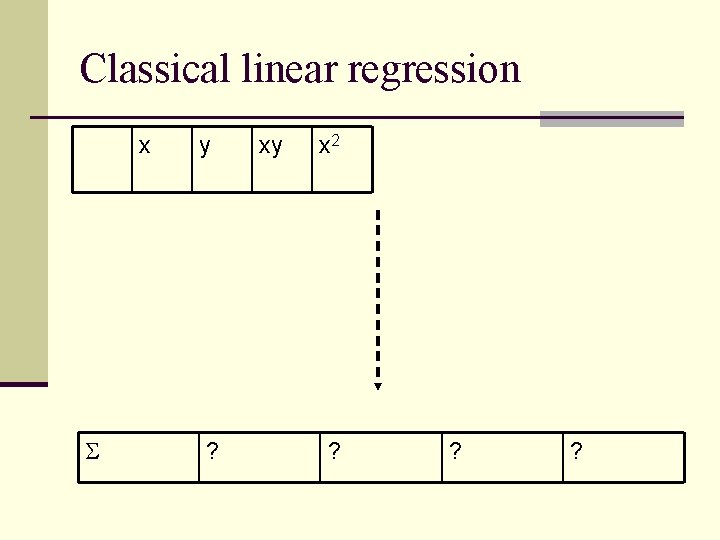
Classical linear regression x y ? xy x 2 ? ? ?

Classical linear regression n Classical linear regression only considered errors in the Y values of the data. n How can we consider errors in both x and y values? n Use Reduced major axis regression

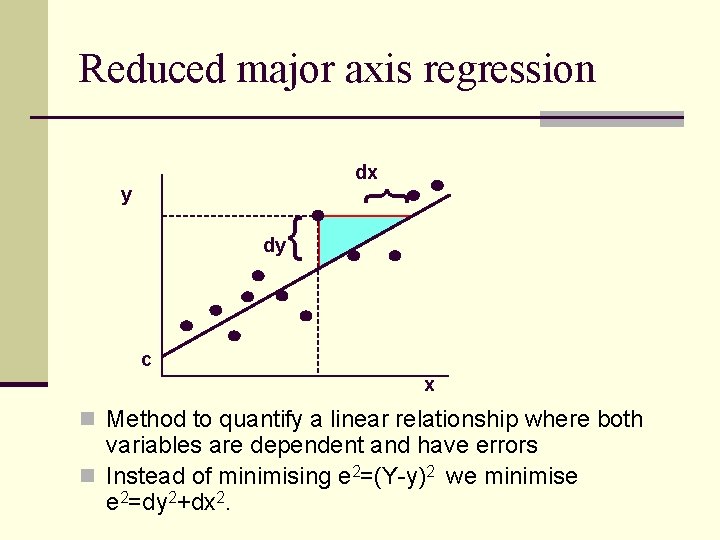
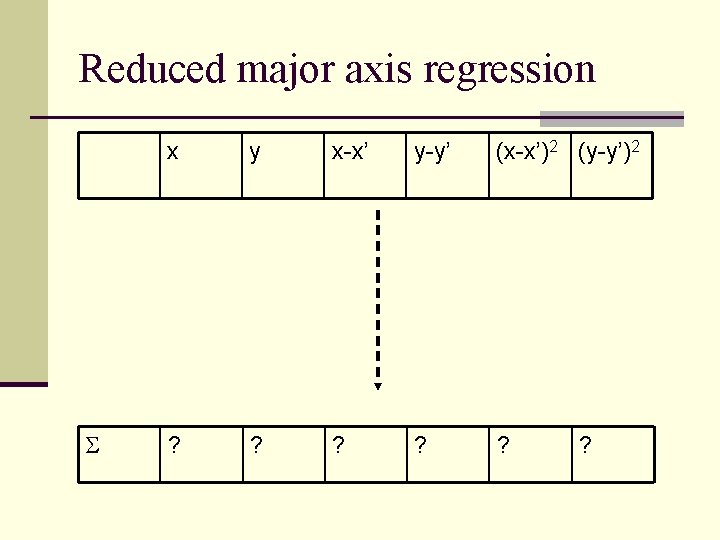
Reduced major axis regression dx { y dy { c x n Method to quantify a linear relationship where both variables are dependent and have errors n Instead of minimising e 2=(Y-y)2 we minimise e 2=dy 2+dx 2.

Reduced major axis regression

Reduced major axis regression x y x-x’ y-y’ (x-x’)2 (y-y’)2 ? ? ?

Error propagation n Every measurement of a variable has an error. n Often the error quoted is one standard deviation of the mean (mean ± standard deviation) n The standard deviation of the sample mean is usually our best estimate of the population standard deviation

Error propagation n Error propagation is a way of combining two or more random errors together to get a third. The equations assume that the errors are Gaussian in nature. n It can be used when you need to measure more than one quantity to get at your final result. For example, if you wanted to predict permeability from a measured porosity and grainsize. The equations introduced here let you propagate the uncertainties on your data through the calculation and come up with an uncertainty on your results. n How then do we combine variables which have errors?

Error propagation - quoted Relationship Error propagation (k=constant)

Example of propagation of error n Suppose we measure thickness of a rock bed using a tape measure. n The tape measure is shorter then the bed thickness so we have to do it in two steps x and y. n We repeat the measurements 100 times and obtain the following mean and standard deviation values for x and y: x=12. 1± 0. 3 cm y=4. 2± 0. 2 cm n The thickness of the bed should be simply: x+y=16. 3 cm n But what about the error on the total thickness?

Example of propagation of error n It is given by propagating the individual errors as follows: n So the final answer for the total thickness of the bed is: 16. 3± 0. 4 cm n Error propagation formulae are non-intuitive and understanding how they are derived requires some mathematical knowledge

More complex examples n What if we have several functions of several variables? n E. g. calculating density using Archimedes Principle: n This equation contains two functions and two variables n Error propagation is best done in parts, so first work out value and error in denominator: n Then the value and error of: n In a few of weeks we will use a Monte Carlo method for solving more complex functions

Reminder Statistics practical #2 n Those not taking BIOL 20451: Roscoe 3. 5 1100 – 1300 Tuesday n Those taking BIOL 20451: Williamson 1. 12 1400 – 1600 Tuesday

Some common problems n Weighted mean f x

What does adding two variables really mean?