EART 162 PLANETARY INTERIORS Francis Nimmo F Nimmo

EART 162: PLANETARY INTERIORS Francis Nimmo F. Nimmo EART 162 Spring 10

Last week - Seismology • Seismic velocities tell us about interior properties • Adams-Williamson equation allows us to relate density directly to seismic velocities • Travel-time curves can be used to infer seismic velocities as a function of depth • Midterm F. Nimmo EART 162 Spring 10

This Week – Fluid Flow & Convection • • Fluid flow and Navier-Stokes Simple examples and scaling arguments Post-glacial rebound Rayleigh-Taylor instabilities What is convection? Rayleigh number and boundary layer thickness See Turcotte and Schubert ch. 6 F. Nimmo EART 162 Spring 10

Viscosity • Young’s modulus gives the stress required to cause a given deformation (strain) – applies to a solid • Viscosity is the stress required to cause a given strain rate – applies to a fluid • Viscosity is basically the fluid’s resistance to flow elastic Young’s modulus viscosity • Kinematic viscosity h measured in Pa s • [Dynamic viscosity n=h/r measured in m 2 s-1] • Typical values for viscosity: water 10 -3 Pa s, basaltic lava 104 Pa s, ice near melting 1014 Pa s, mantle 1021 Pa s • Viscosity often temperature-dependent (see Week 3) F. Nimmo EART 162 Spring 10

Defining Viscosity • Recall • Viscosity is the stress generated for a given strain rate • Example – moving plate: u h d (Shear) stress s required to generate velocity gradient u / d (= ) Viscosity h=s d / u • Example – moving lava flow: Driving shear stress = rgd sinq a d Surface velocity = rgd 2 sinq / h e. g. Hawaiian flow h=104 Pa s q=5 o d=3 m -1 (walking pace) gives u=2 ms q F. Nimmo EART 162 Spring 10

Adding in pressure • In 1 D, shear stress (now using t) is • Let’s assume u only varies in the y direction Viscous force (x direction, Fluid velocity u y per unit volume): dy x dx Pressure force (x direction, per unit volume): Why the minus sign? F. Nimmo EART 162 Spring 10

Putting it together • Total force/volume = viscous + pressure effects • We can use F=ma to derive the response to this force What does this mean? • So the 1 D equation of motion in the x direction is What does each term represent? • In the y-direction, we would also have to add in buoyancy forces (due to gravity) F. Nimmo EART 162 Spring 10

Navier-Stokes • We can write the general (3 D) formula in a more compact form given below – the Navier-Stokes equation • The formula is really a mnemonic – it contains all the physics you’re likely to need in a single equation • The vector form given here is general (not just Cartesian) Yuk! Inertial term. Pressure Source of turbulence. gradient See next slide. Buoyancy force (e. g. Diffusion-like viscosity Zero for steadythermal or electromagnetic) term. Warning: is state flows is a unit vector complicated, especially in non-Cartesian geom. F. Nimmo EART 162 Spring 10

Reynolds number • Is the inertial or viscous term more important? • We can use a scaling argument to get the ratio Re: a Re Here L is a characteristic lengthscale of the problem • Re is the Reynolds number and tells us whether a flow is turbulent (inertial forces dominate) or not • Fortunately, many geological situations allow us to neglect inertial forces (Re<<1) • E. g. what is Re for the convecting mantle? F. Nimmo EART 162 Spring 10

Example 1 – Channel Flow L y 0 x u P 2 P 1 2 d (Here u doesn’t vary in x-direction) • 2 D channel, steady state, u=0 at y=+d and y=-d a • Max. velocity (at centreline) = (DP/L) d 2/2 h • Does this result make sense? • We could have derived a similar answer from a scaling argument – how? F. Nimmo EART 162 Spring 10

Example 2 – falling sphere r Steady-state. What are the important terms? a u h An order of magnitude argument gives drag force ~ hur Is this dimensionally correct? The full answer is 6 phur, first derived by George Stokes in 1851 (apparently under exam conditions) By balancing the drag force against the excess weight of the sphere (4 pr 3 Drg/3 ) we can obtain the terminal velocity (here Dr is the density contrast between sphere and fluid) F. Nimmo EART 162 Spring 10

Example 3 – spreading flow y h(x, t) u d x Low Re, roughly steady-state. What are the important terms? Conservation of mass gives (why? ) As long as d >>h, we get: a What kind of equation is this? Does it make physical sense? Where might we apply it on Earth? F. Nimmo EART 162 Spring 10

Postglacial Rebound ice w L mantle • Postglacial rebound problem: How long does it take for the mantle to rebound? • Two approaches: – Scaling argument – Stream function j – see T&S • Scaling argument: • Assume u is constant (steady flow) and that u ~ dw/dt • We end up with decay constant • What does this equation mean? a F. Nimmo EART 162 Spring 10

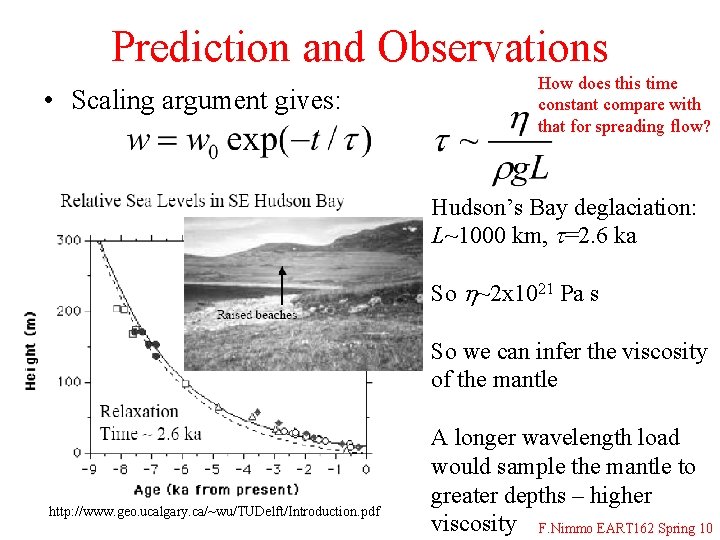
Prediction and Observations • Scaling argument gives: How does this time constant compare with that for spreading flow? Hudson’s Bay deglaciation: L~1000 km, t=2. 6 ka So h~2 x 1021 Pa s So we can infer the viscosity of the mantle http: //www. geo. ucalgary. ca/~wu/TUDelft/Introduction. pdf A longer wavelength load would sample the mantle to greater depths – higher viscosity F. Nimmo EART 162 Spring 10

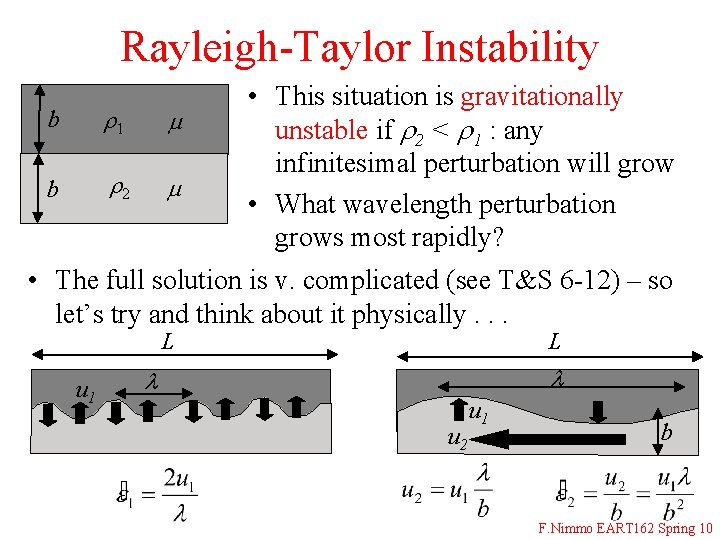
Rayleigh-Taylor Instability b r 1 m b r 2 m • This situation is gravitationally unstable if r 2 < r 1 : any infinitesimal perturbation will grow • What wavelength perturbation grows most rapidly? • The full solution is v. complicated (see T&S 6 -12) – so let’s try and think about it physically. . . L u 1 L l l u 2 u 1 b F. Nimmo EART 162 Spring 10

R-T Instability (cont’d) • Recall from Week 5: dissipation per unit volume • We have two contributions to total dissipation ( • By adding the two contributions, we get ) term a term • What wavelength minimizes the dissipation? • We end up with dissipation minimized at lmin=1. 26 b • This compares pretty well with the full answer (2. 57 b) and saves us about six pages of maths F. Nimmo EART 162 Spring 10

R-T instability (cont’d) • The layer thickness determines which wavelength minimizes viscous dissipation • This wavelength is the one that will grow fastest • So surface features (wavelength) tell us something about the interior structure (layer thickness) Salt domes in S Iran. Dome spacing of ~15 km suggests salt layer thickness of ~5 km, in agreement with seismic observations ~50 km F. Nimmo EART 162 Spring 10

Convection Cold - dense • Convection arises because fluids expand decrease in density when heated Fluid • The situation on the right is gravitationally unstable – hot fluid will tend to rise • But viscous forces oppose fluid motion, so Hot - less dense there is a competition between viscous and (thermal) buoyancy forces • So convection will only initiate if the buoyancy forces are big enough • What is the expression for thermal buoyancy forces? F. Nimmo EART 162 Spring 10

Conductive heat transfer • Diffusion equation (1 D, Cartesian) Advected Conductive component Heat production • Thermal diffusivity k=k/r. Cp (m 2 s-1) • Diffusion timescale: F. Nimmo EART 162 Spring 10

Convection equations • There are two: one controlling the evolution of temperature, the other the evolution of velocity • They are coupled because temperature affects flow (via buoyancy force) and flow affects temperature (via the advective term) Navier. Stokes Thermal Evolution Buoyancy force Note that here the N-S equation is neglecting the inertial term Advective term • It is this coupling that makes solving convection problems hard F. Nimmo EART 162 Spring 10

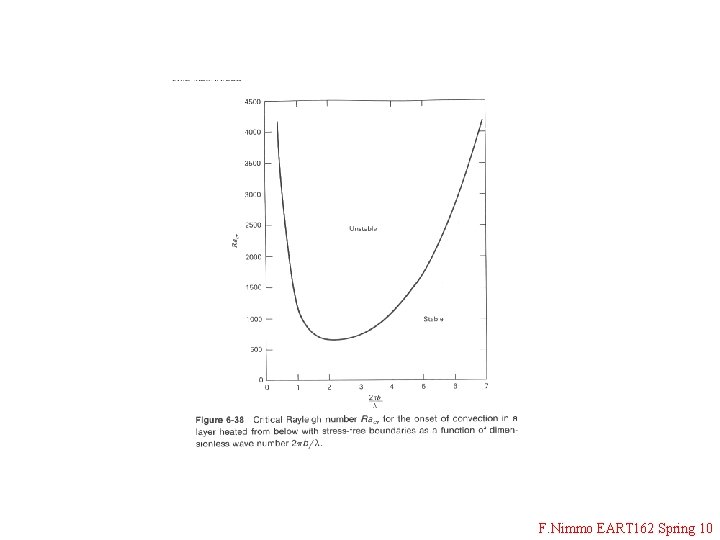
Initiation of Convection • Recall buoyancy forces favour motion, viscous forces oppose it d • Another way of looking at the problem is there are two competing timescales – what are they? a Top temperature T 0 d Incipient upwelling Hot layer Bottom temp. T 1 • Whether or not convection occurs is governed by the dimensionless (Rayleigh) number Ra: • Convection only occurs if Ra is greater than the critical Rayleigh number, ~ 1000 (depends a bit on. F. Nimmo geometry) EART 162 Spring 10

Constant viscosity convection • Convection results in hot and cold boundary layers and an isothermal interior • In constant-viscosity convection, top and bottom b. l. have same thickness • • cold T 0 (T 0+T 1)/2 d Isothermal interior hot T 1 d d T 1 Heat is conducted across boundary layers In the absence of convection, heat flux So convection gives higher heat fluxes than conduction The Nusselt number defines the convective efficiency: F. Nimmo EART 162 Spring 10

Boundary layer thickness d • We can balance the timescale for conductive thickening of the cold boundary layer against the timescale for the cold blob to descend to obtain an expression for the b. l. thickness d: d d a • So the boundary layer gets thinner as convection becomes more vigorous • Also note that d is independent of d. Why? • We can therefore calculate the convective heat flux: F. Nimmo EART 162 Spring 10

Example - Earth • Does this equation make sense? • Plug in some parameters for the terrestrial mantle: r=3000 kg m-3, g=10 ms-2, a=3 x 10 -5 K-1, k=10 -6 m 2 s-1, h=3 x 1021 Pa s, k=3 W m-1 K-1, (T 1 -T 0) =1500 K • We get a convective heat flux of 170 m. Wm-2 • This is about a factor of 2 larger than the actual terrestrial heat flux (~80 m. Wm-2) – not bad! • NB for other planets (lacking plate tectonics), d tends to be bigger than these simple calculations would predict, and the convective heat flux smaller • Given the heat flux, we can calculate thermal evolution F. Nimmo EART 162 Spring 10

Summary • Fluid dynamics can be applied to a wide variety of geophysical problems • Navier-Stokes equation describes fluid flow: • Post-glacial rebound timescale: • Behaviour of fluid during convection is determined by a single dimensionless number, the Rayleigh number Ra F. Nimmo EART 162 Spring 10

End of lecture • Supplementary material follows F. Nimmo EART 162 Spring 10

Thermodynamics & Adiabat • A packet of convecting material is often moving fast enough that it exchanges no energy with its surroundings • What factors control whether this is true? • As the convecting material rises, it will expand (due to reduced pressure) and thus do work (W = P d. V) • This work must come from the internal energy of the material, so it cools • The resulting change in temperature as a function of pressure (d. T/d. P) is called an adiabat • Adiabats explain e. g. why mountains are cooler than valleys F. Nimmo EART 162 Spring 10

Adiabatic Gradient (1) • If no energy is added or taken away, the entropy of the system stays constant • Entropy S is defined by Here d. Q is the amount of energy added to the system (so if d. Q=0, then d. S=0 also and the system is adiabatic) • What we want is at constant S. How do we get it? • We need some definitions: Specific heat capacity (at constant P) Thermal expansivity Maxwell’s identity F. Nimmo EART 162 Spring 10

T Adiabatic Gradient (2) • We can assemble these pieces to get the z adiabatic temperature gradient: adiabat • NB You’re not going to be expected to reproduce the derivation, but you do need to learn the final result • An often more useful expression can be obtained by converting pressure to depth (how? ) a • What are typical values for terrestrial planets? F. Nimmo EART 162 Spring 10

Incompressibility & Stream Function • In many fluids the total volume doesn’t change dx dy u(x) v(y) u(x+dx) a v(y+dy) If V 1=V 2 then Incompressibility condition • We can set up a stream function j which automatically satisfies incompressibility and describes both the horizontal and the vertical velocities: Note that these satisfy incompressibility F. Nimmo EART 162 Spring 10

Stream Function j • Only works in 2 dimensions • Its usefulness is we replace u, v with one variable j Check signs here! Differentiate LH eqn. w. r. t. z and RH w. r. t x a The velocity field of any 2 D viscous flow satisfies this equation F. Nimmo EART 162 Spring 10

Postglacial rebound and j (1) • Biharmonic equation for viscous fluid flow • Assume (why? ) j is a periodic function j=sin kx Y(y) Here k is the wavenumber = 2 p/l • After a bit of algebra, we get a • All that is left (!) is to determine the constants which are set by the boundary conditions – in real problems, this is often the hardest bit • What are the boundary conditions? • u=0 at z=0, v=dw/dt at z=0, u=v=0 at large z F. Nimmo EART 162 Spring 10

Postglacial rebound and j (2) • Applying the boundary conditions we get a • We have dw/dt = : 1 • Vert. viscous stress at surface (z=0) balances deformation: Why can we ignore this term? • For steady flow, we can derive P from Navier-Stokes a 2 • Finally, eliminating A from 1 and 2 we get (at last!): This ought to look familiar. . . F. Nimmo EART 162 Spring 10

Postglacial rebound (concluded) • So we get exponential decay of topography, with a time constant depending on wavenumber (k) and viscosity (h) • Same result as we got with the scaling argument! • Relaxation time depends on wavelength of load • Relaxation time depends on viscosity of fluid F. Nimmo EART 162 Spring 10

Convection Cold - dense • Convection arises because fluids expand decrease in density when heated Fluid • The situation on the right is gravitationally unstable – hot fluid will tend to rise • But viscous forces oppose fluid motion, so Hot - less dense there is a competition between viscous and (thermal) buoyancy forces • So convection will only initiate if the buoyancy forces are big enough • Note that this is different to the Rayleigh-Taylor case: thermal buoyancy forces decay with time (diffusion), compositional ones don’t • What is the expression for thermal buoyancy F. Nimmo forces? EART 162 Spring 10

F. Nimmo EART 162 Spring 10

Two Dimensions. . . • In 1 D, shear stress (now using t) is x txy v y • In 2 D, there are three different stresses: txy Shear stress txx u Normal stresses tyy • Where do the factors of 2 come from? p(y)dx p(x)dy dy dx p(y+dy)dx • Force due to pressure (x direction, per unit cross-sectional area): p(x+dx)dy a 1 F. Nimmo EART 162 Spring 10

Viscous forces on an element (1) x y txy v u dy dx tyy txx • Viscous force (x direction, per unit cross-sectional area): a 2 • Total force balance given by viscous + pressure forces 1 + 2 • After some algebra, we get total force in x-direction: a Note that force in x-direction only depends on velocity in x-direction and the x-gradient of pressure F. Nimmo EART 162 Spring 10

Viscous forces on an element (2) • In the y-direction, body forces can also be important • Otherwise, the analysis is the same as before • We can use F=ma to derive the response to this force What does this mean? • So the equations of motion in x and y directions are F. Nimmo EART 162 Spring 10

Putting it together • x-direction • y-direction Pressure gradient • Special cases: Viscous terms Body force – Steady-state – Du/Dt=0 – One-dimension (e. g. v=0, u only varies in y direction) F. Nimmo EART 162 Spring 10