Each element has been assigned a unique one

• Each element has been assigned a unique one-, two-, or three-letter symbol for its identification • The first letter of a symbol is always capitalized • Only recently discovered elements that don’t yet have permanent names are given three-letter symbols • Uncombined elements are written as monatomic (without a subscript) – Examples: Fe, C, Al • Diatomic elements – 2 of the same atoms (HOFBr. INCl’s) – Examples: H 2, O 2

• The atomic mass of an element is given in atomic mass units (amu) • Found on the periodic table • The mass of 1 mole of an element is equal to its atomic mass (periodic table) in grams

• The sum of the atomic masses of its atoms Example: CO 2 =

Mass Examples • Find the atomic or formula mass of the following substances: (To the nearest tenth) 1. 2. 3. 4. 5. 6. C Br Cl 2 H 2 O Ca 3 PO 4 Ca(OH)2

• The mass of 1 mole of the substance • Measured in grams Example: 1. 0 mole of CO 2 = 44 g

• Use the gram formula mass to convert between moles and mass Examples: 1. 1. 5 moles of CO 2 = _______ g 2. 24 g of C = _______ moles 3. 3. 0 moles of Br = _______ g 4. 5. 0 g of Al = _______ moles

• If you have an ideal gas at standard temperature and pressure (STP) – 0 o. C and 1 atm 1 mole = 22. 4 L

Mole – Volume Examples 1. 1. 5 moles of CO 2 (g) = _______ L 2. 38 L of Ne(g) = _______ moles 3. 3. 0 moles of O 2(g) = _______ L 4. 11 L of N 2(g) = _______ moles

• 1 dozen = 12 • 1 mole = 6. 02 x 1023 (Avagadro’s Number) • How big is a mole? – 602, 000, 000, 000 – A mole of marbles would spread over the surface of the earth, and produce a layer about 50 miles thick – A mole of sand, spread over the United States, would produce a layer 3 inches deep – A mole of dollars could not be spent at the rate of a billion dollars a day over a trillion years

• He stated that equal volumes of all gases at the same temperature and pressure contain the same number of molecules (Acogadro’s Principle) • Later his work led to the realization Amedeo Avogadro that a molecular mass in grams (mole) of any substance contains the same number of molecules (6. 02 x 1023)

1 mole of atoms = 6. 02 x 1023 atoms 1 mole of particles = 6. 02 x 1023 particles 1 mole of molecules = 6. 02 x 1023 molecules 1 mole of compounds = 6. 02 x 1023 compounds

Mole – Number Examples 1. 4. 00 moles of Na. Cl = _______ molecules 2. 0. 50 mole of Mg. Br 2 = _______ molecules 3. 3. 01 x 1023 Na. Cl molecules = _______ moles 4. 6. 02 x 1021 Zn atoms = _______ moles

Empirical Formulas • Represents the simplest integer ratio in which the atoms combine to form a compound (the reduced form) • All ionic formulas are written as empirical formulas

Molecular Formulas • The actual numbers of the atoms in a molecule • May be a multiple of the empirical formula Examples: • What are the empirical formulas of the following molecules? a. H 2 O 2 b. C 6 H 12 O 6 c. CCl 4

Percent Composition • Composition in terms of the percentage of each component present Example: H 2 SO 4 – Step 1: Calculate the formula mass of H 2 SO 4 – Step 2: Find the percent mass of each element

Percent Mass Example • Calculate the percent composition of oxygen in CO 2

Water of Hydration • Percentage of water in the crystal – Hydrate – a compound that contains water – Anyhdrous – hydrate without the water

Water of Hydration Example • Find the water of hydration in Cu. SO 4 5 H 20 • Step 1 - Find the formula mass • Step 2 - Percentage of water

Water of Hydration Example • Calculate the water of hydration in Na 2 CO 3 10 H 2 O

Determining Mass Ratios from Formulas • Example: Find the mass ratio for a compound with the empirical formula CH 2.

Determining the Molecular Formula from the mass and the empirical formula A compound has a molecular mass of 180 amu and an empirical formula of CH 2 O. What is its molecular formula? • Step 1: Determine the molecular mass of the empirical formula • Step 2: Divide the molecular mass of the compound by the mass of the empirical formula. • Step 3: Multiply the subscripts in the empirical formula by your answer to step 2

Determining the empirical formula from percent composition What is the empirical formula of a compound that consists of 58. 80% barium, 13. 75% sulfur, and 27. 45% oxygen by mass? • Step 1: Assume that the mass of the sample is 100 g • Step 2: Convert the masses into moles • Step 3: Find the smallest whole numbers ratio (divide each number from step 2 by the smallest one)

Chemical Reactions • Reactant – Substance that enters into a reaction, written to the left of the arrow, starting material • Product – substance that is produced by the reaction, written to the right of the arrow, end material • Example: HCl + Na. OH Na. Cl + H 2 O – Reactants: – Products:

• Reaction that requires energy (heat) in order to occur – heat enters • Heat is absorbed • Heat is a reactant • Surroundings will feel cold because heat has been absorbed from the surroundings • Example: H 2 O(s) + heat H 2 O(l)

• Reaction that produce energy (heat) when they occur – heat exits • Heat is released, given off • Heat is a product • Surroundings will feel hot because heat was released to the surroundings • Example: H 2 O(l) H 2 O(s) + heat

ü Synthesis ü Decomposition ü Single Replacement ü Double Replacement

• Direct combination • Substances combine to form a new compound • Produces 1 product Examples: A + B AB 2 H 2(g) + O 2(g) 2 H 2 O(l)

• Break down of a compound into simpler parts • Starts with 1 reactant Examples: AB A + B 2 H 2 O(l) 2 H 2(g) + O 2(g)

• One substances switches spots with another • Element + compound makes a new element plus a new compound Examples: A + BC B + AC Cu(s) + 2 Ag. NO 3(aq) 2 Ag(s) + Cu(NO 3)2 *copper replaces silver

• Exchange of ions • Everything gets a new "partner" • Compound + compound makes new compound + new compound Examples: AB + CD AD + CB Ag. NO 3(aq) + Na. Cl(aq) Ag. Cl(s) + Na. NO 3(aq)

Balancing Equations • Coefficient - a number, placed before formulas to indicate the ratios of moles involved in a reaction • Equations must be balanced in accordance with the Law of Conservation of Mass • The mass of both sides of the arrow must be equal • You must have an equal number of each type of atom on both sides of the equation Example: 2 H 2 + O 2 2 H 2 O

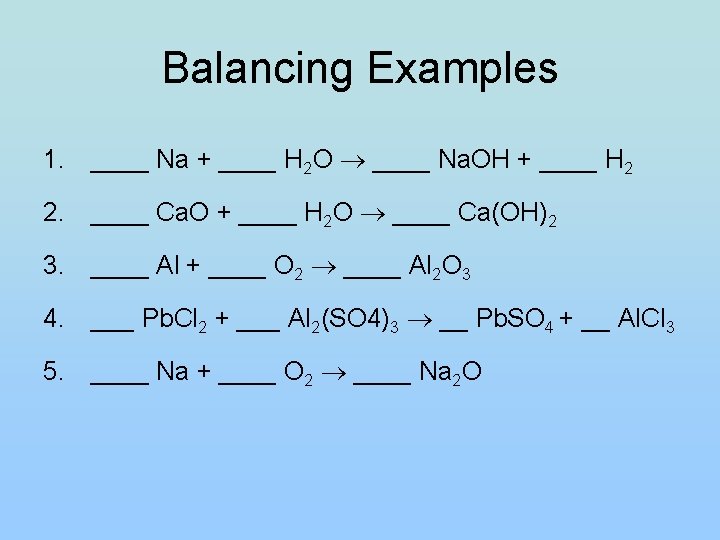
Balancing Examples 1. ____ Na + ____ H 2 O ____ Na. OH + ____ H 2 2. ____ Ca. O + ____ H 2 O ____ Ca(OH)2 3. ____ Al + ____ O 2 ____ Al 2 O 3 4. ___ Pb. Cl 2 + ___ Al 2(SO 4)3 __ Pb. SO 4 + __ Al. Cl 3 5. ____ Na + ____ O 2 ____ Na 2 O

Determining the Missing Mass in Equations If 103. 0 g of potassium chlorate (KCl. O 3) are decomposed to form 62. 7 g of potassium chloride (KCl) and oxygen gas (O 2) according to the equation 2 KCl. O 3 2 KCl + 3 O 2, how many grams of oxygen are formed? (Hint: Remember the mass of the products must equal the mass of the reactants)

How many grams of Fe are needed to react with 8. 0 g of O 2 to produce 28. 9 g of Fe 3 O 4 according to the equation 3 Fe + 2 O 2 Fe 3 O 4?

Equation Problems • Using the balanced equations and mole conversions you can solve for variety of problems • Remember that the coefficients used represent mole ratios

Given the following reaction answer the questions below: 2 C 2 H 6 + 7 O 2 4 CO 2 + 6 H 2 O 1. How many moles of CO 2 are produced when 2. 0 moles of C 2 H 6 reacts? 2. How many moles of H 2 O are produced when 4. 0 moles of C 2 H 6 reacts? 3. How many moles of H 2 O are produced when 5. 0 moles of C 2 H 6 combusts?

Given the following reaction: ____ H 2 + ____ Cl 2 _____ HCl 1. The production of 37 g of HCl would require how many moles of H 2? 2. If 20. L of H 2 completely reacts how many grams of HCl would be produced?

Use the balanced equation to answer the questions below: ____ C 2 H 4 + ____ O 2 ____ CO 2 + ____ H 2 O 1. How many liters of O 2 are used to produce 1. 0 mole of H 2 O? 2. How many liters of CO 2 are produced when 9. 00 liters of O 2 is consumed? 3. How many liters of C 2 H 4 are needed to produce 10. 0 liters of CO 2?