Dynamics Unit Vocabulary Dynamics The study of Forces

Dynamics Unit Vocabulary: Dynamics: The study of Forces and their interactions with matter. Force: (F) A push or a pull. (A vector quantity, has magnitude and direction. ) Inertial Mass: (m) The property of matter that makes it resist being accelerated. Gravitational Mass: (m) The property of matter that makes it attract other matter at a distance. Weight: (w) The force of gravity on an object W = mg Weight = mass * acceleration of gravity 1 Newton = (kg) * (m/s 2)

Dynamics Unit Newton’s Laws of Motion Newton’s First Law- INERTIA An object at rest will remain at rest and an object in motion will remain in motion unless acted on by an unbalanced force. Newton’s Second Law – FNET = ma Newton’s Third Law – Action-Reaction For every applied force there is an equal and opposite reaction force.

Bell Warmer A sprinter accelerates uniformly from rest for 4 seconds. If the sprinter covers a distance of 40 m, find the acceleration of the sprinter and the final velocity of the sprinter.

a) How much force would you have to apply to a 50 kg mass on a surface with a coefficient of static friction of 0. 8 to make the mass move? b) If the mass above has a coefficient of kinetic friction of 0. 3, at what rate would the mass accelerate after it starts sliding (assume the same force continues to be applied. )

d=? Height of window = 1 m A bald alien visiting Earth sees a flower pot fall past their window and notices that it took 0. 25 seconds to travel from the top of the window to the bottom. Find d (the distance between the bottom of the top window and the top of the bottom window. )

100 N 50 kg d=? A constant force of 100 N acts on a 50 kg mass for 10 seconds. If the mass started from rest, a)How far will it move during the ten seconds? b)How fast will it be moving at the end of 10 seconds?

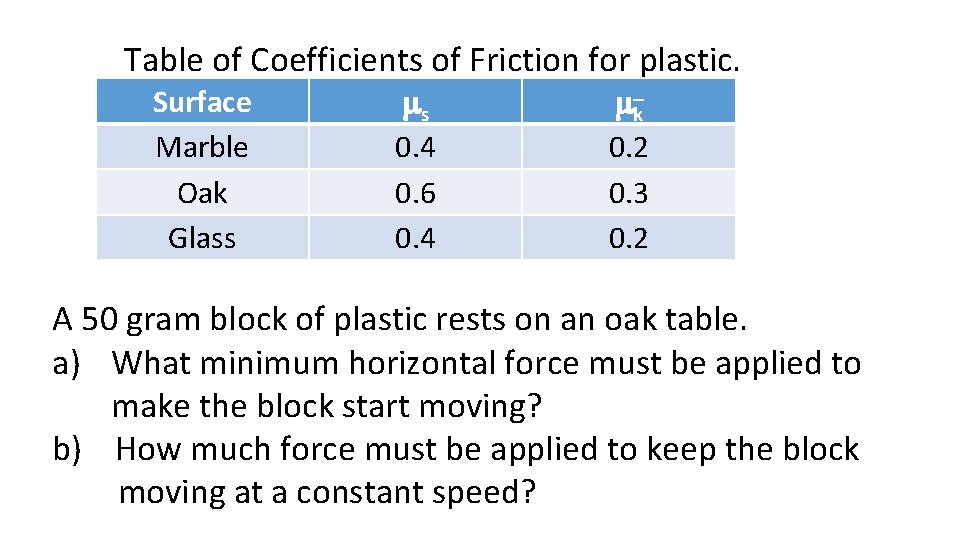
Table of Coefficients of Friction for plastic. Surface Marble Oak Glass ms 0. 4 0. 6 0. 4 mk 0. 2 0. 3 0. 2 A 50 gram block of plastic rests on an oak table. a) What minimum horizontal force must be applied to make the block start moving? b) How much force must be applied to keep the block moving at a constant speed?

Dynamics Unit Vocabulary: Centripetal Acceleration: Acceleration of an object with a velocity that is changing direction. (Always directed inward toward the center of the circular motion, perpendicular to the velocity. ) Equilibrium: An object is at equilibrium when its acceleration is zero. (That includes when the velocity is constant. ) Free Body Diagram: A diagram of one body in a system showing all the forces that act on that body.

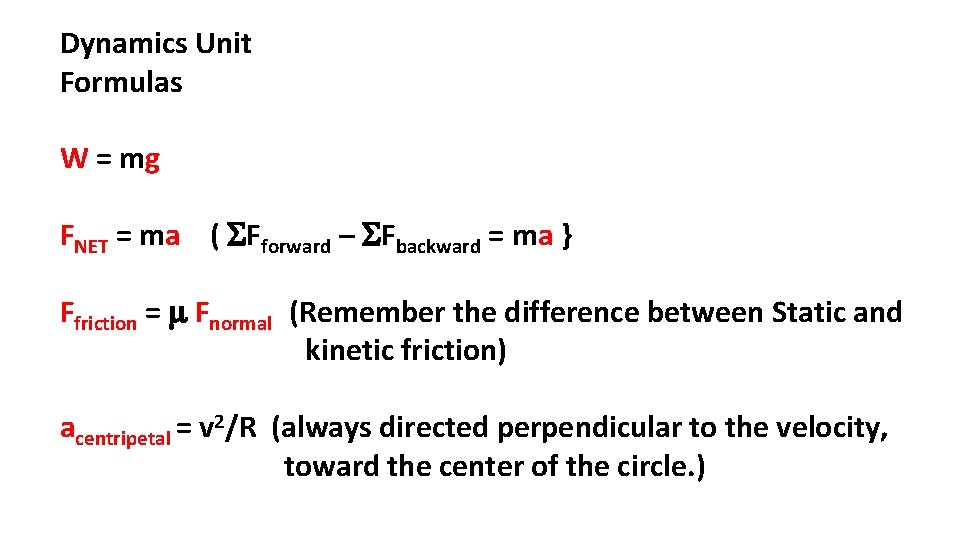
Dynamics Unit Formulas W = mg FNET = ma ( SFforward – SFbackward = ma } Ffriction = m Fnormal (Remember the difference between Static and kinetic friction) acentripetal = v 2/R (always directed perpendicular to the velocity, toward the center of the circle. )

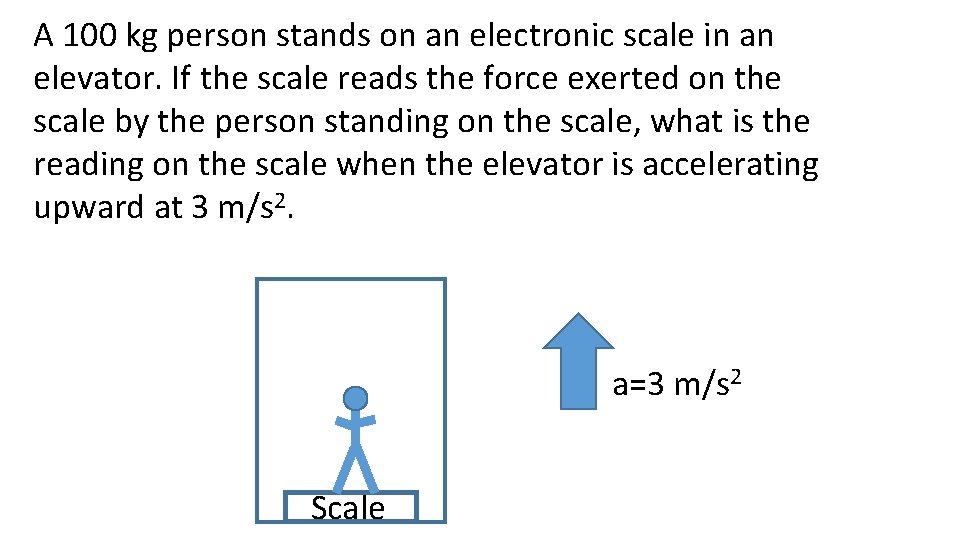
A 100 kg person stands on an electronic scale in an elevator. If the scale reads the force exerted on the scale by the person standing on the scale, what is the reading on the scale when the elevator is accelerating upward at 3 m/s 2. a=3 m/s 2 Scale

1. Draw Free Body Diagram. 2. Resolve any oblique forces into x and y components 3. Use Newton’s 2 nd Law to consider the forces and acceleration in the y direction. nd 4. Use Newton’s 2 Law to consider the forces and acceleration in the x direction

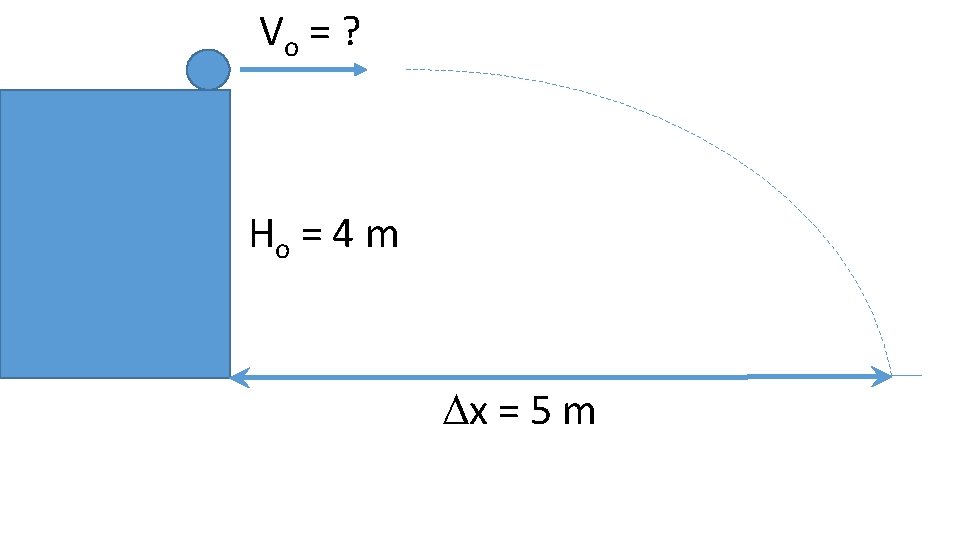
Vo = ? Ho = 4 m Dx = 5 m

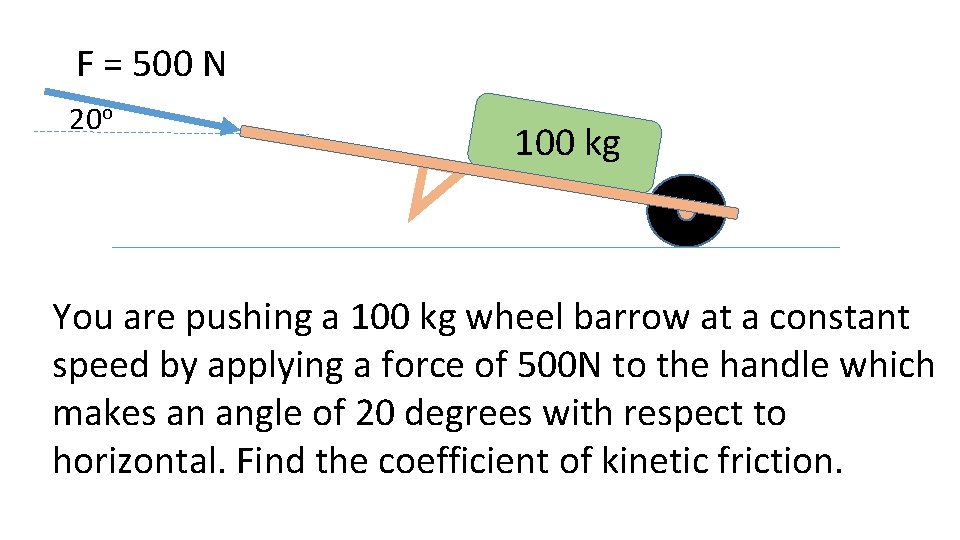
F = 500 N 20 o 100 kg You are pushing a 100 kg wheel barrow at a constant speed by applying a force of 500 N to the handle which makes an angle of 20 degrees with respect to horizontal. Find the coefficient of kinetic friction.

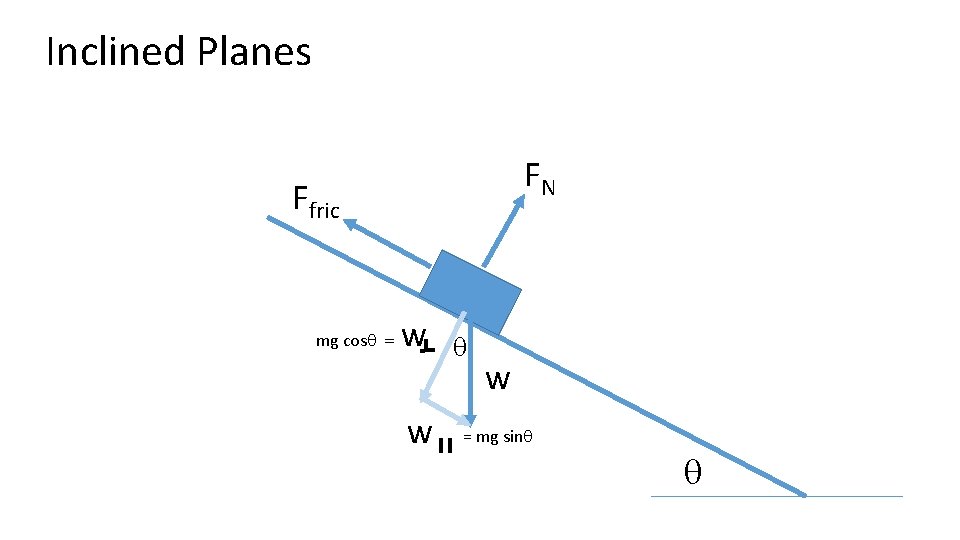
Inclined Planes FN Ffric mg cosq = w w q w = mg sinq q

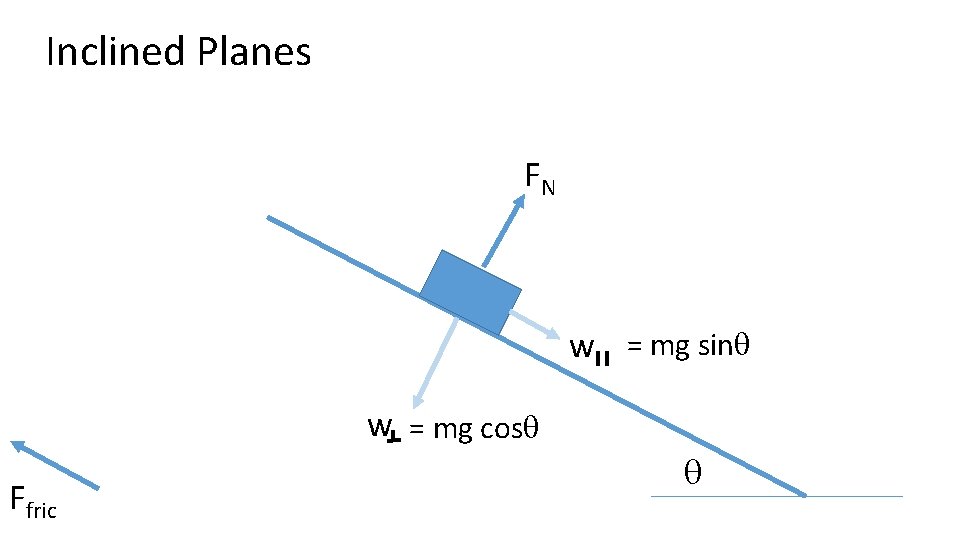
Inclined Planes FN w = mg sinq w = mg cosq Ffric q

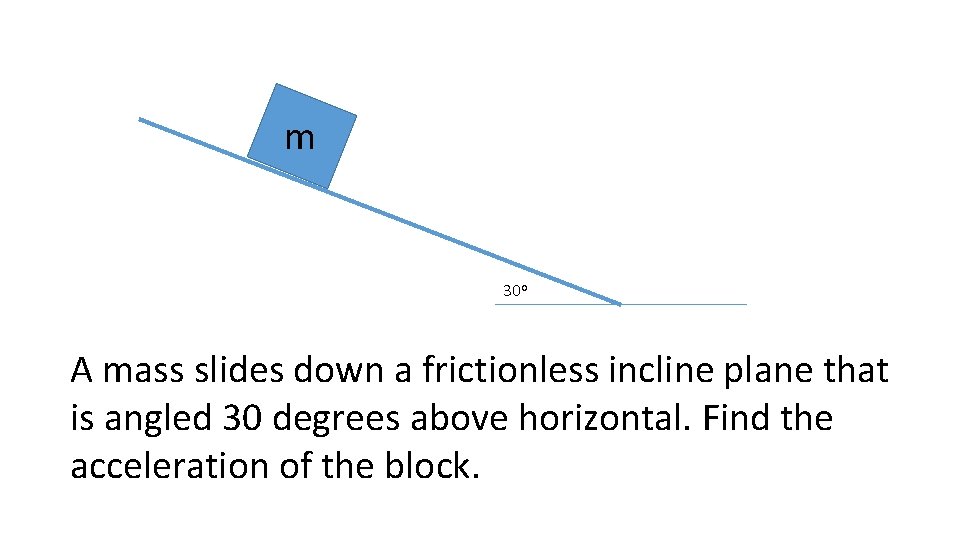
m 30 o A mass slides down a frictionless incline plane that is angled 30 degrees above horizontal. Find the acceleration of the block.

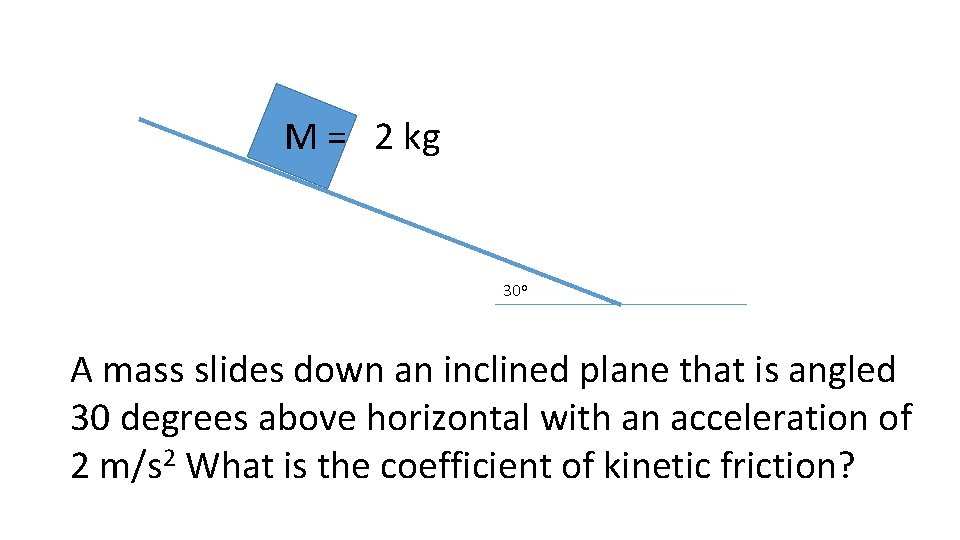
M = 2 kg 30 o A mass slides down an inclined plane that is angled 30 degrees above horizontal with an acceleration of 2 m/s 2 What is the coefficient of kinetic friction?

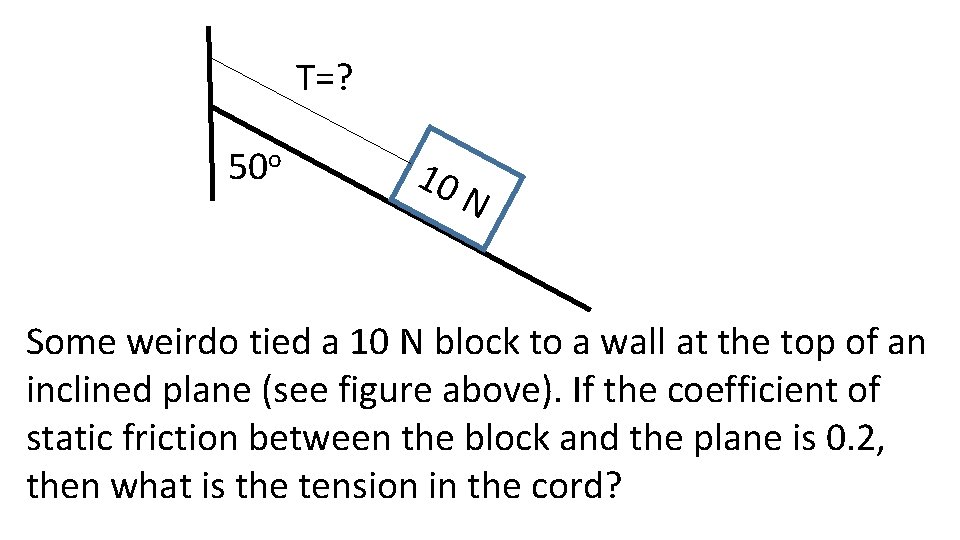
T=? 50 o 10 N Some weirdo tied a 10 N block to a wall at the top of an inclined plane (see figure above). If the coefficient of static friction between the block and the plane is 0. 2, then what is the tension in the cord?

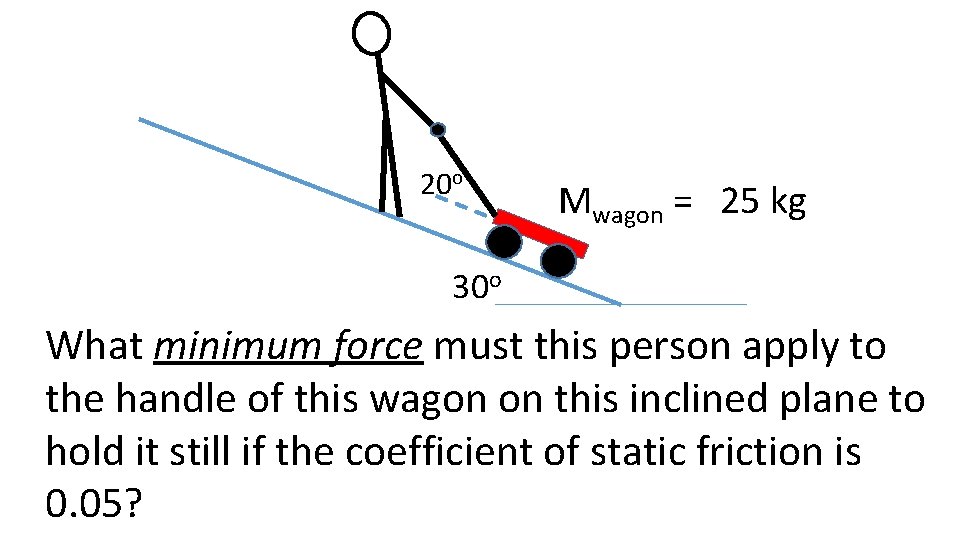
20 o Mwagon = 25 kg 30 o What minimum force must this person apply to the handle of this wagon on this inclined plane to hold it still if the coefficient of static friction is 0. 05?

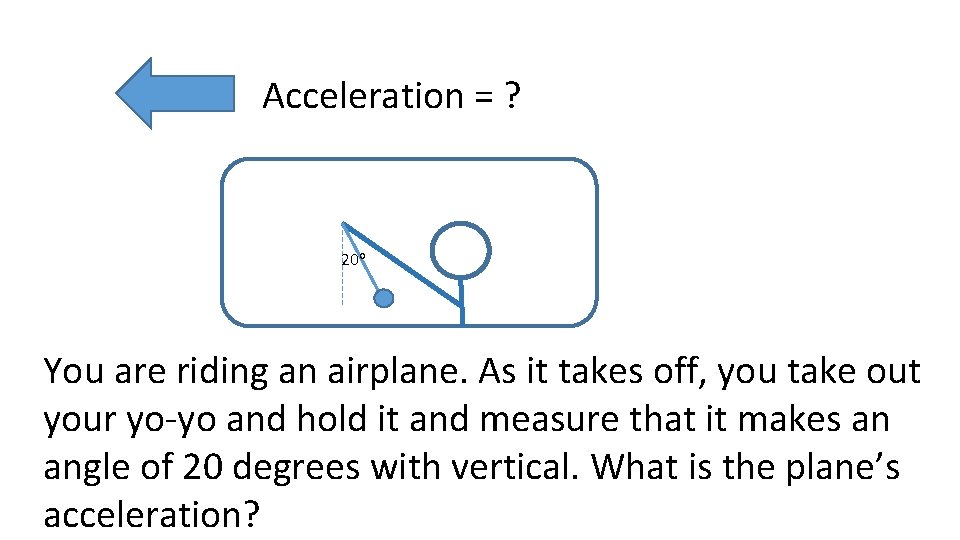
Acceleration = ? 20 o You are riding an airplane. As it takes off, you take out your yo-yo and hold it and measure that it makes an angle of 20 degrees with vertical. What is the plane’s acceleration?

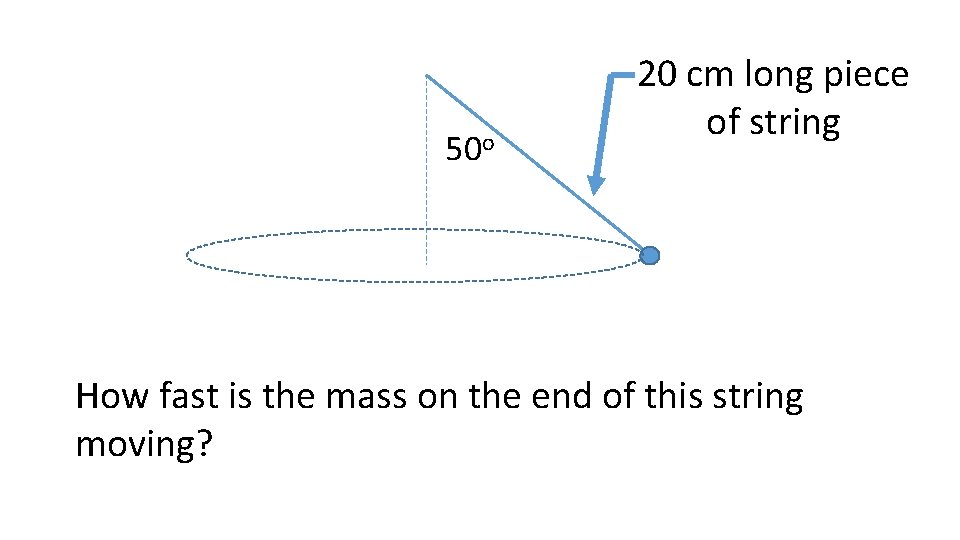
50 o 20 cm long piece of string How fast is the mass on the end of this string moving?

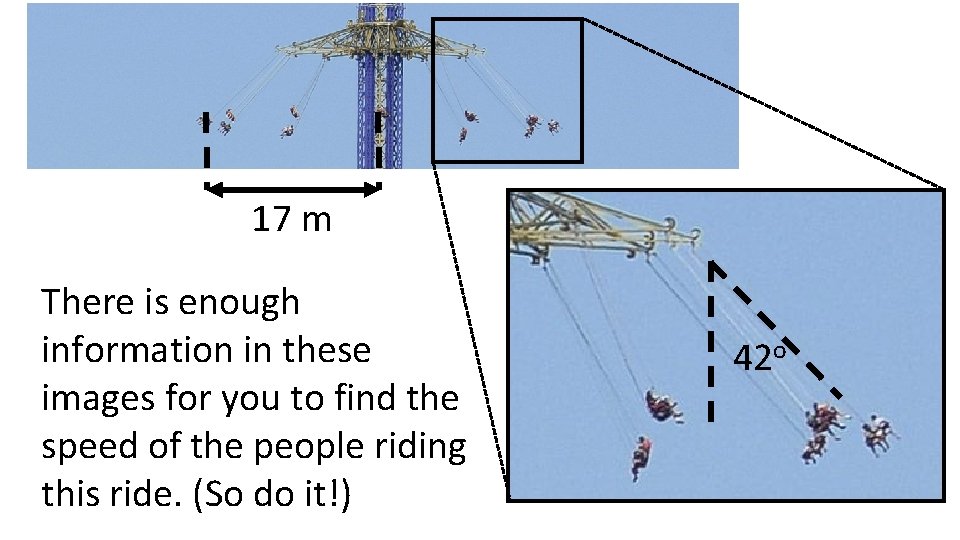
17 m There is enough information in these images for you to find the speed of the people riding this ride. (So do it!) 42 o

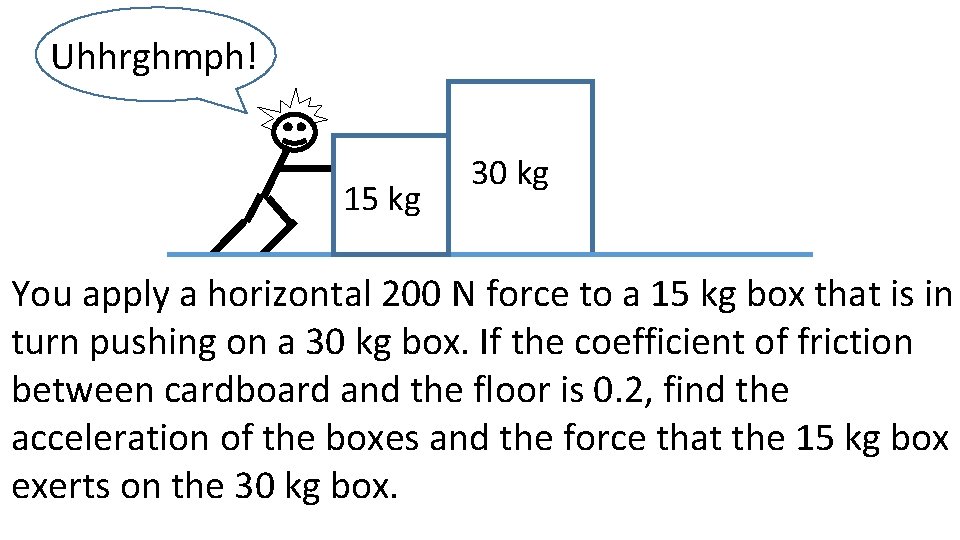
Uhhrghmph! 15 kg 30 kg You apply a horizontal 200 N force to a 15 kg box that is in turn pushing on a 30 kg box. If the coefficient of friction between cardboard and the floor is 0. 2, find the acceleration of the boxes and the force that the 15 kg box exerts on the 30 kg box.

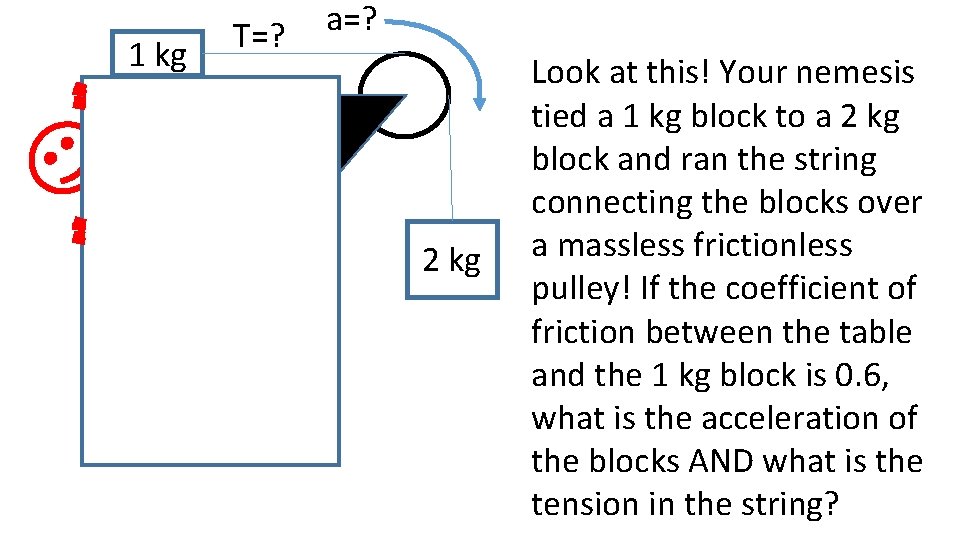
1 kg T=? a=? 2 kg Look at this! Your nemesis tied a 1 kg block to a 2 kg block and ran the string connecting the blocks over a massless frictionless pulley! If the coefficient of friction between the table and the 1 kg block is 0. 6, what is the acceleration of the blocks AND what is the tension in the string?

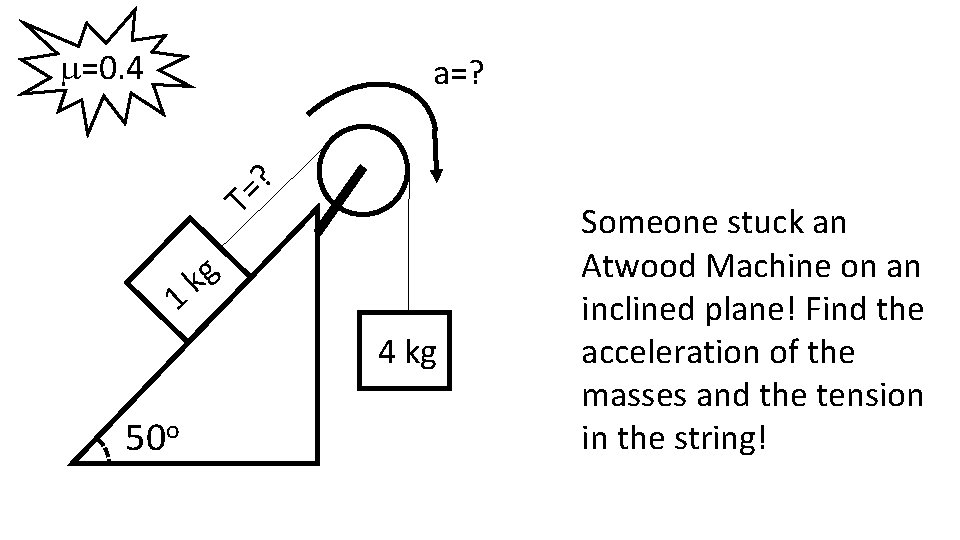
m=0. 4 a=? ? = T g k 1 4 kg 50 o Someone stuck an Atwood Machine on an inclined plane! Find the acceleration of the masses and the tension in the string!

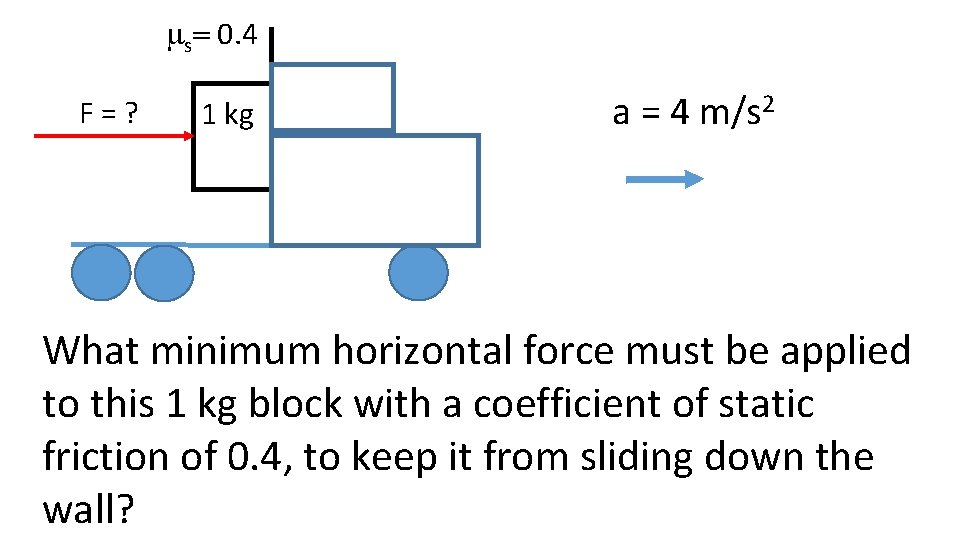
ms= 0. 4 F=? 1 kg a = 4 m/s 2 What minimum horizontal force must be applied to this 1 kg block with a coefficient of static friction of 0. 4, to keep it from sliding down the wall?

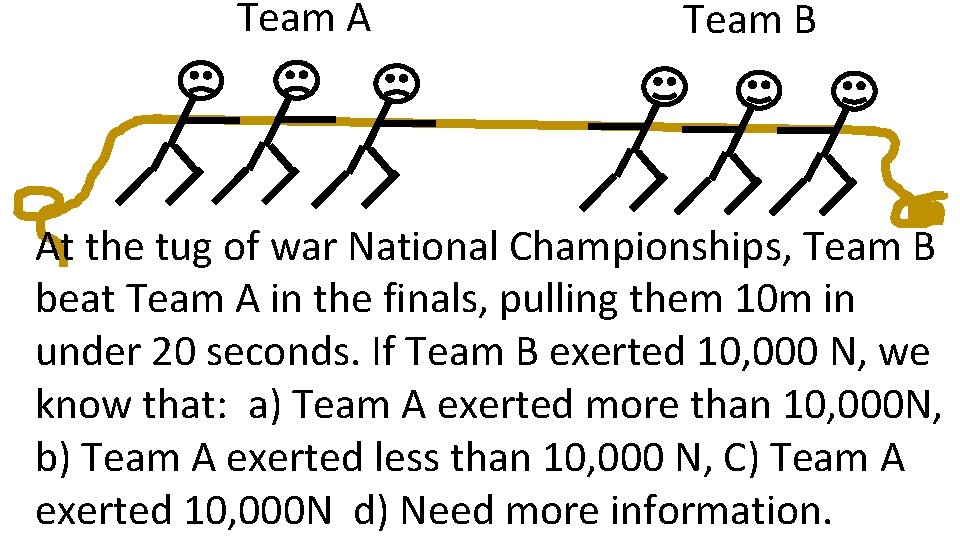
Team A Team B At the tug of war National Championships, Team B beat Team A in the finals, pulling them 10 m in under 20 seconds. If Team B exerted 10, 000 N, we know that: a) Team A exerted more than 10, 000 N, b) Team A exerted less than 10, 000 N, C) Team A exerted 10, 000 N d) Need more information.

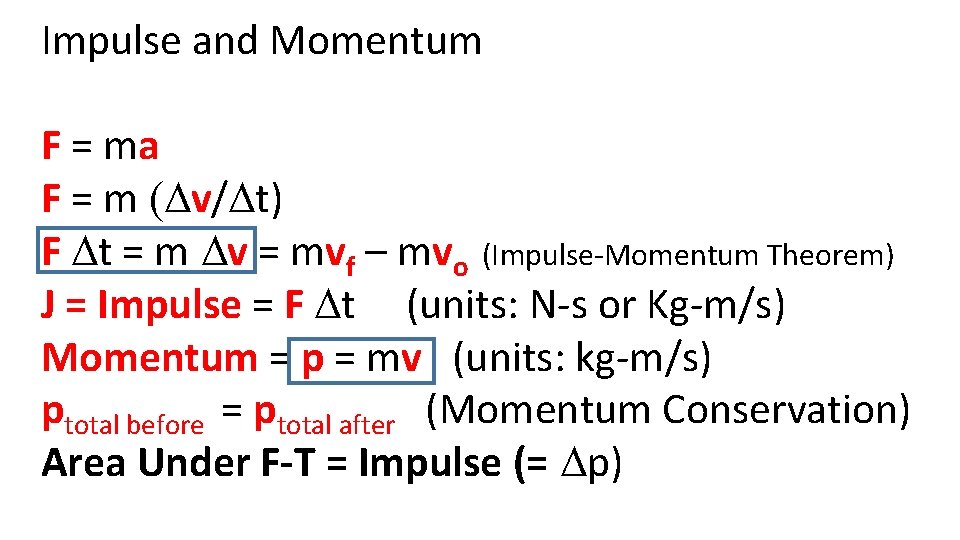
Impulse and Momentum F = ma F = m (Dv/Dt) F Dt = m Dv = mvf – mvo (Impulse-Momentum Theorem) J = Impulse = F Dt (units: N-s or Kg-m/s) Momentum = p = mv (units: kg-m/s) ptotal before = ptotal after (Momentum Conservation) Area Under F-T = Impulse (= Dp)

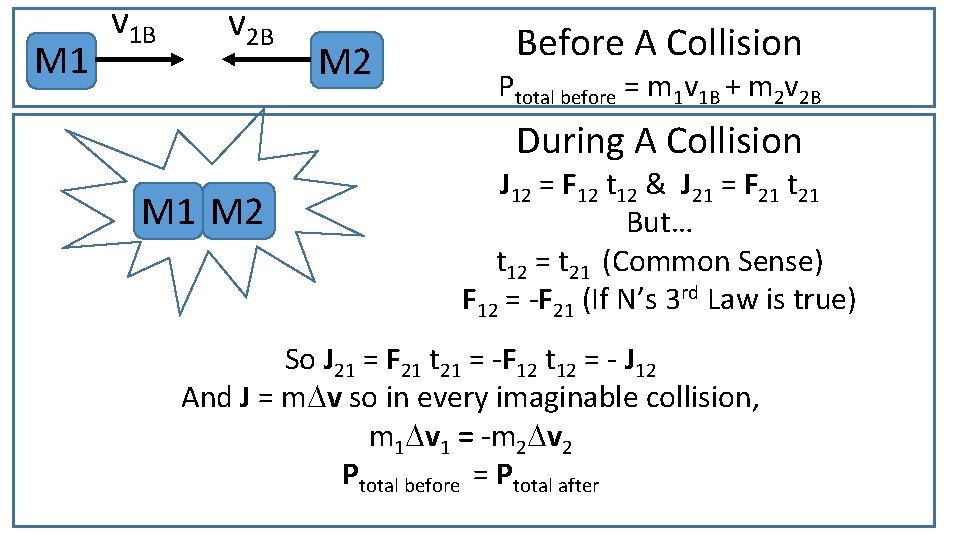
M 1 v 1 B v 2 B M 2 Before A Collision Ptotal before = m 1 v 1 B + m 2 v 2 B During A Collision M 1 M 2 J 12 = F 12 t 12 & J 21 = F 21 t 21 But… t 12 = t 21 (Common Sense) F 12 = -F 21 (If N’s 3 rd Law is true) So J 21 = F 21 t 21 = -F 12 t 12 = - J 12 And J = m. Dv so in every imaginable collision, m 1 Dv 1 = -m 2 Dv 2 Ptotal before = Ptotal after

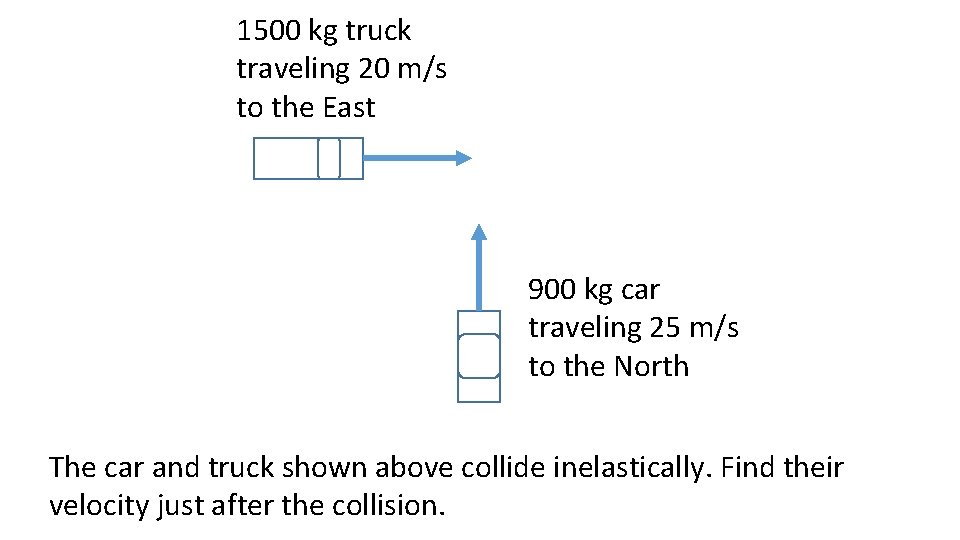
1500 kg truck traveling 20 m/s to the East 900 kg car traveling 25 m/s to the North The car and truck shown above collide inelastically. Find their velocity just after the collision.

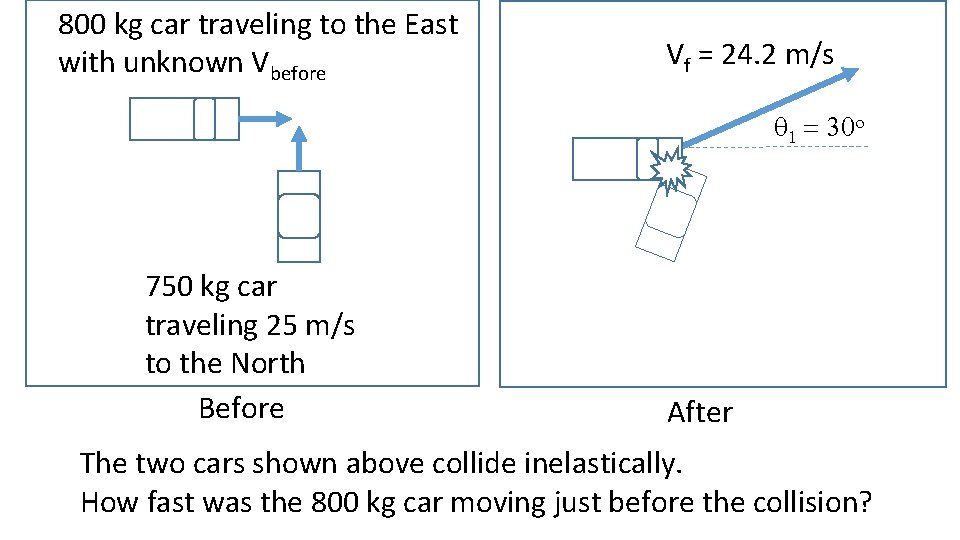
800 kg car traveling to the East with unknown Vbefore Vf = 24. 2 m/s q 1 = 30 o 750 kg car traveling 25 m/s to the North Before After The two cars shown above collide inelastically. How fast was the 800 kg car moving just before the collision?

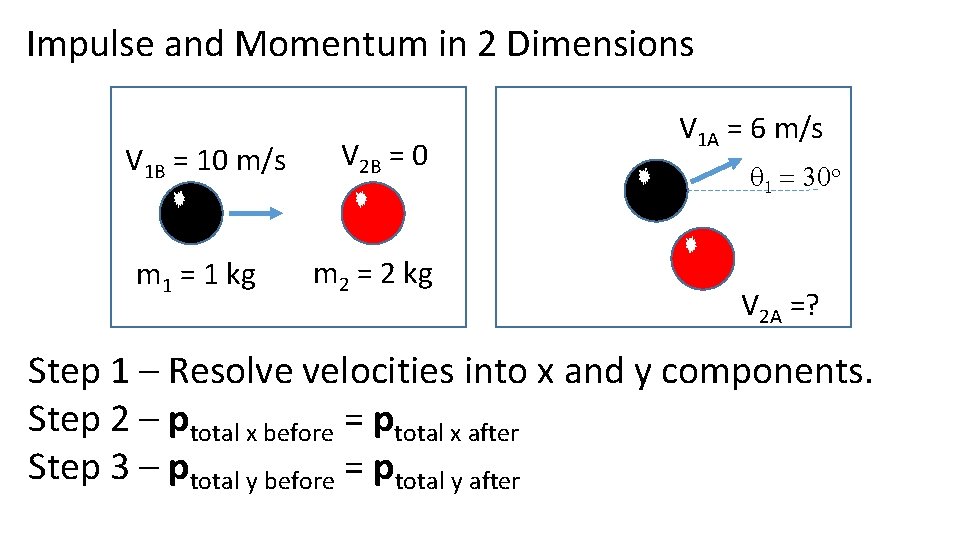
Impulse and Momentum in 2 Dimensions V 1 B = 10 m/s m 1 = 1 kg V 2 B = 0 m 2 = 2 kg V 1 A = 6 m/s q 1 = 30 o V 2 A =? Step 1 – Resolve velocities into x and y components. Step 2 – ptotal x before = ptotal x after Step 3 – ptotal y before = ptotal y after

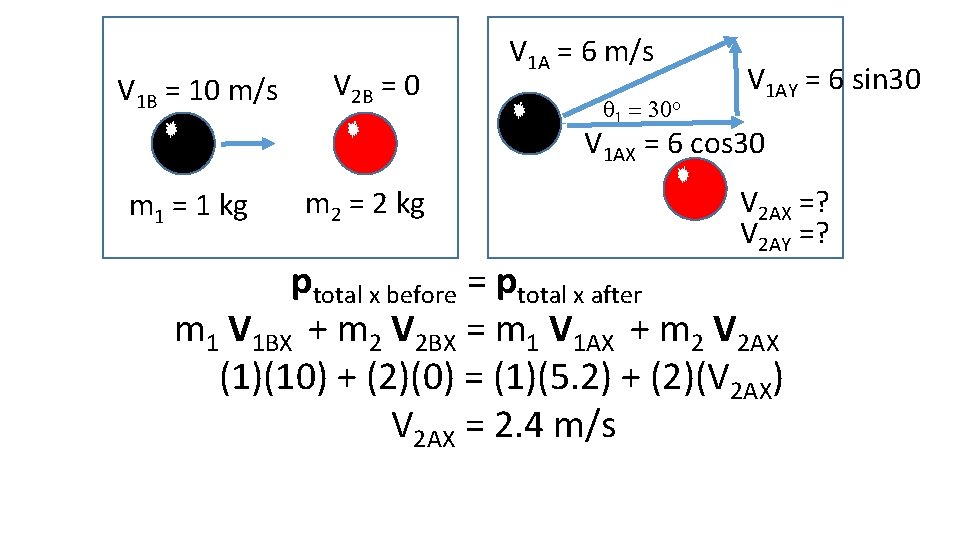
V 1 B = 10 m/s V 2 B = 0 V 1 A = 6 m/s q 1 = 30 o V 1 AY = 6 sin 30 V 1 AX = 6 cos 30 m 1 = 1 kg m 2 = 2 kg V 2 AX =? V 2 AY =? ptotal x before = ptotal x after m 1 V 1 BX + m 2 V 2 BX = m 1 V 1 AX + m 2 V 2 AX (1)(10) + (2)(0) = (1)(5. 2) + (2)(V 2 AX) V 2 AX = 2. 4 m/s

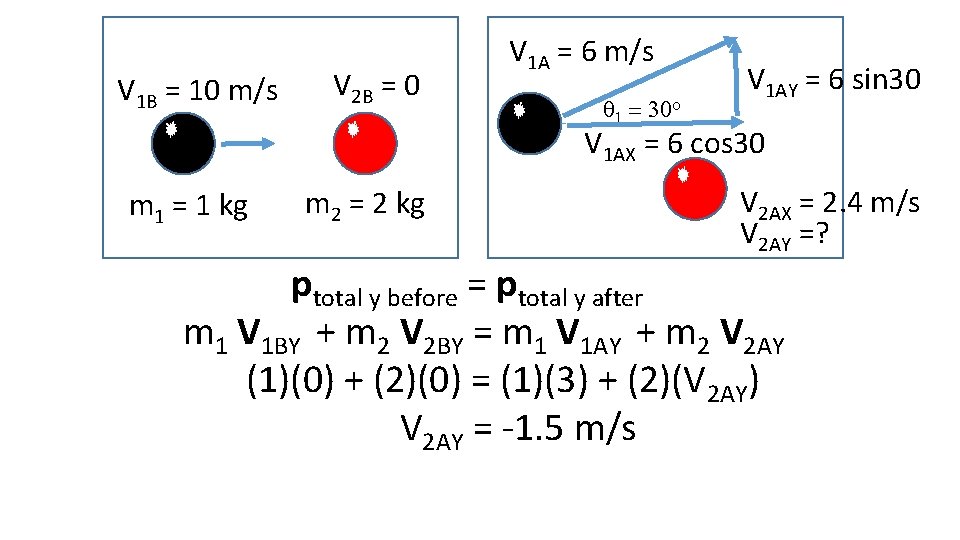
V 1 B = 10 m/s V 2 B = 0 V 1 A = 6 m/s q 1 = 30 o V 1 AY = 6 sin 30 V 1 AX = 6 cos 30 m 1 = 1 kg m 2 = 2 kg V 2 AX = 2. 4 m/s V 2 AY =? ptotal y before = ptotal y after m 1 V 1 BY + m 2 V 2 BY = m 1 V 1 AY + m 2 V 2 AY (1)(0) + (2)(0) = (1)(3) + (2)(V 2 AY) V 2 AY = -1. 5 m/s

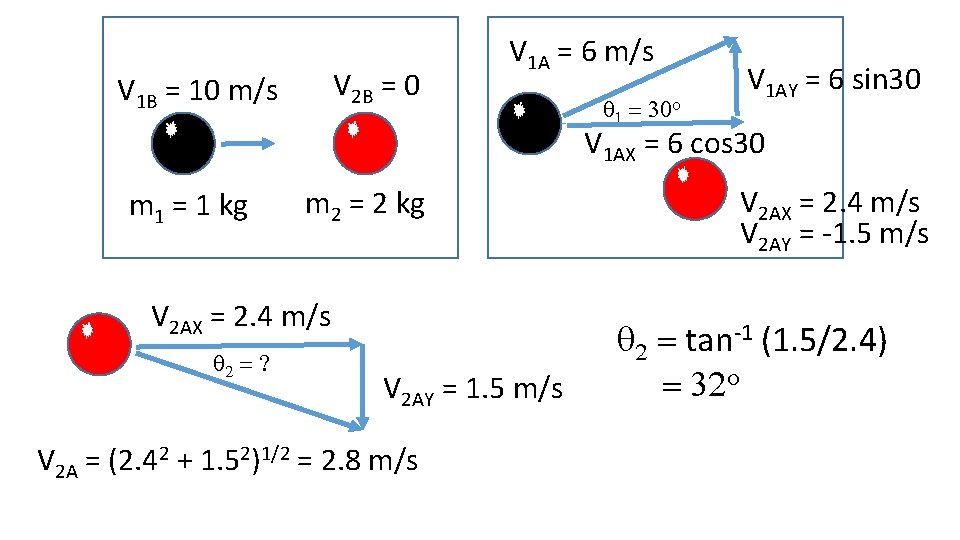
V 2 B = 0 V 1 B = 10 m/s V 1 A = 6 m/s q 1 = 30 o V 1 AY = 6 sin 30 V 1 AX = 6 cos 30 m 1 = 1 kg m 2 = 2 kg V 2 AX = 2. 4 m/s q 2 = ? V 2 AY = 1. 5 m/s V 2 A = (2. 42 + 1. 52)1/2 = 2. 8 m/s V 2 AX = 2. 4 m/s V 2 AY = -1. 5 m/s q 2 = tan-1 (1. 5/2. 4) = 32 o

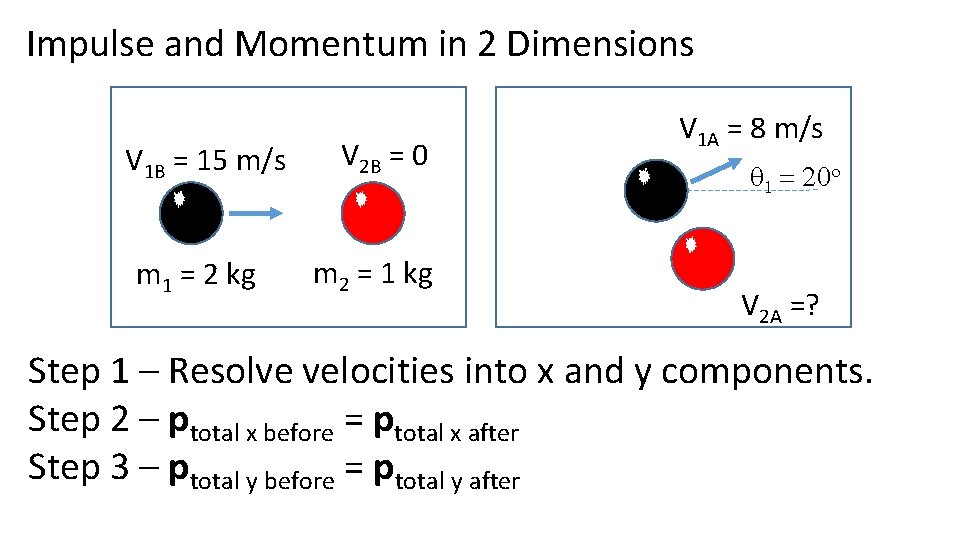
Impulse and Momentum in 2 Dimensions V 1 B = 15 m/s m 1 = 2 kg V 2 B = 0 m 2 = 1 kg V 1 A = 8 m/s q 1 = 20 o V 2 A =? Step 1 – Resolve velocities into x and y components. Step 2 – ptotal x before = ptotal x after Step 3 – ptotal y before = ptotal y after

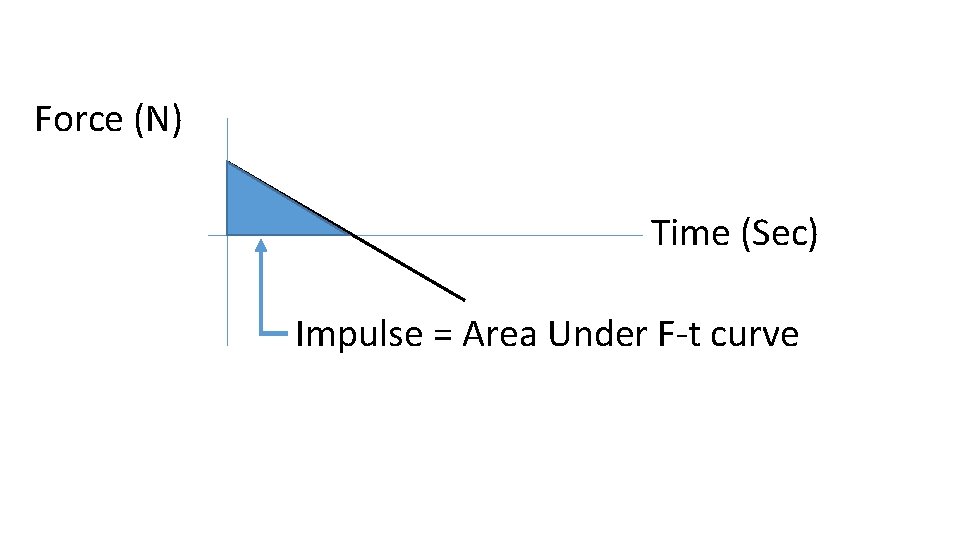
Force (N) Time (Sec) Impulse = Area Under F-t curve

Unit 4 – Work and Energy Vocabulary Energy – the ability to do work. Work = Force Displacement = |F||d|cosq (Scalar) Units: N m = Joule {calories are also units of energy} Power = Work/time (Scalar) Units: Joule/sec = Watt Conservative Force–Force that depends only on position. (Gravity is an example. ) Non-Conservative Force-force that does not depend on only position. (Friction is an example. )

Unit 4 – Work and Energy Vocabulary (Cont’d) Kinetic Energy = KE = (½)mv 2 (energy associated with motion) Gravitational Potential Energy = GPE = mgh Hooke’s Law = Fs = kx (force vs displacement from equilibrium length for an “ideal” spring) Work = Area Under a Force vs Displacement graph. Spring Potential Energy = Us = ½ kx 2 Energy Conservation: Total Engery = KE + GPE + Us Work = DTE

Problem : A 2 kg bouncy ball is dropped from a height of 10 meters, hits the floor and returns to its original height. What was the change in momentum of the ball upon impact with the floor? What was the impulse provided by the floor? http: //www. physicsclassroom. com/calcpad/energy/problems

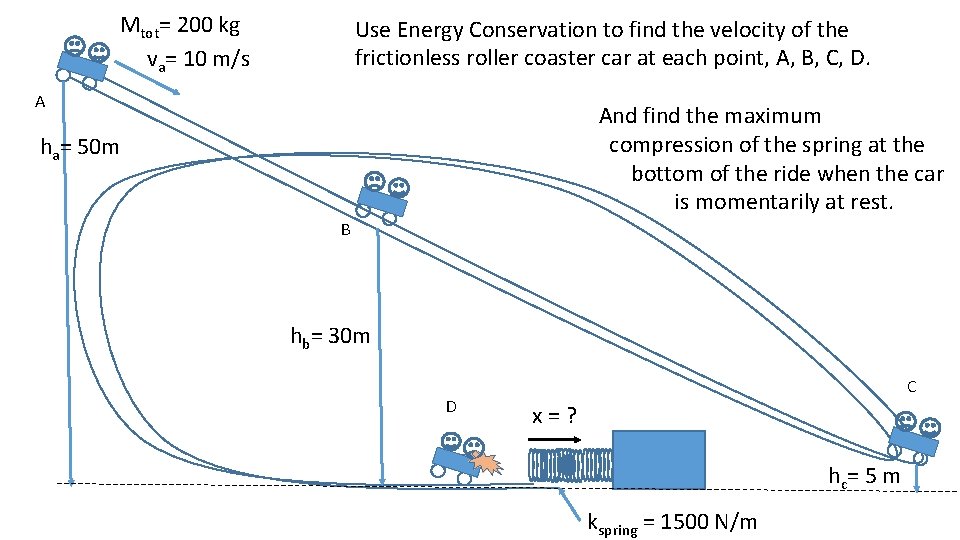
Mtot= 200 kg va= 10 m/s Use Energy Conservation to find the velocity of the frictionless roller coaster car at each point, A, B, C, D. A And find the maximum compression of the spring at the bottom of the ride when the car is momentarily at rest. ha= 50 m B hb= 30 m D C x=? hc = 5 m kspring = 1500 N/m

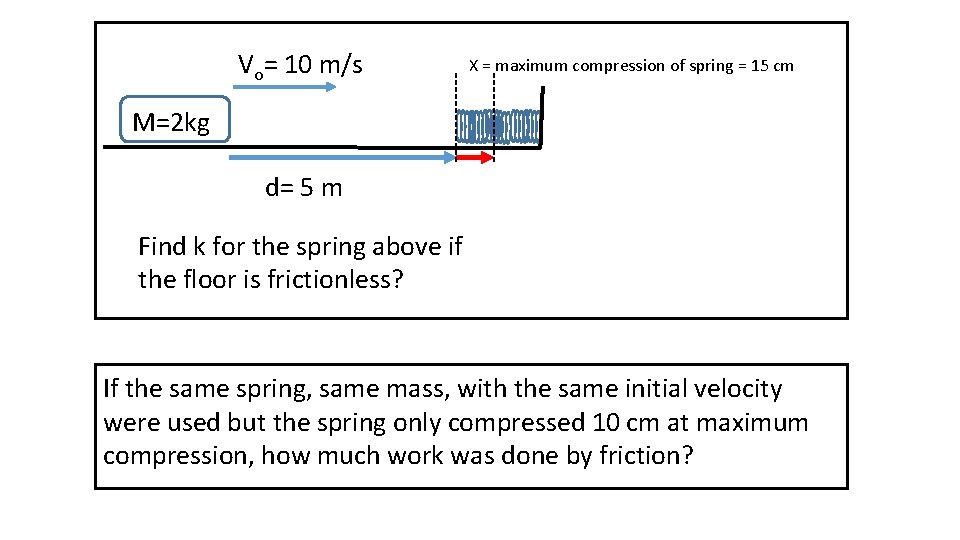
Vo= 10 m/s X = maximum compression of spring = 15 cm M=2 kg d= 5 m Find k for the spring above if the floor is frictionless? If the same spring, same mass, with the same initial velocity were used but the spring only compressed 10 cm at maximum compression, how much work was done by friction?

Unit 4 – Work and Energy Vocabulary (Cont’d) ***A collision is Perfectly Elastic (or Elastic) IF the KETotal before = KETotal after To solve an Elastic Collision problem, use Momentum Conservation to get: Equation 1: m 1 V 1 B + m 2 V 2 B = m 1 V 1 A + m 2 V 2 A THEN use this new formula: Equation 2: V 2 B - V 1 B = V 1 A - V 2 A

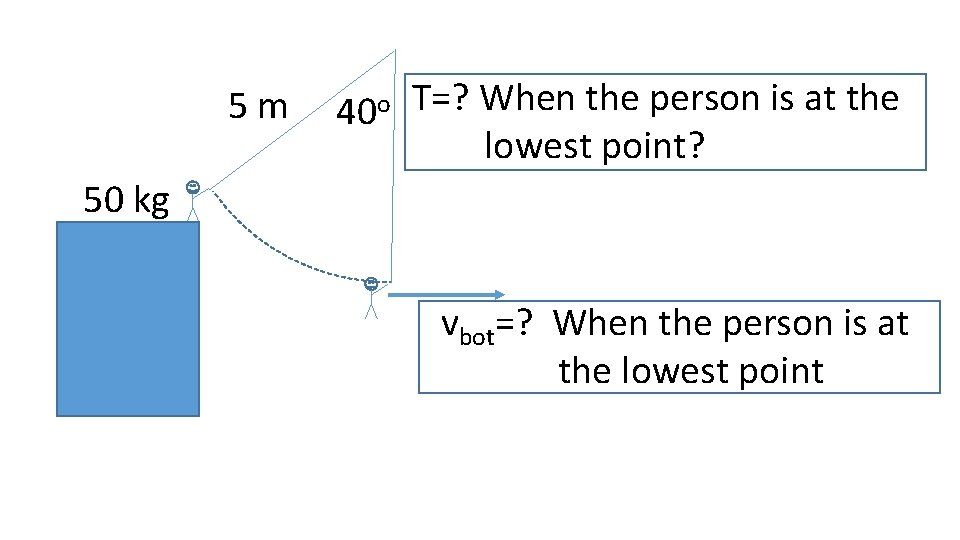
5 m 40 o T=? When the person is at the lowest point? 50 kg vbot=? When the person is at the lowest point