Dynamics of Surface Pattern Evolution in Thin Films

Dynamics of Surface Pattern Evolution in Thin Films Rui Huang Center for Mechanics of Solids, Structures and Materials Department of Aerospace Engineering and Engineering Mechanics The University of Texas at Austin

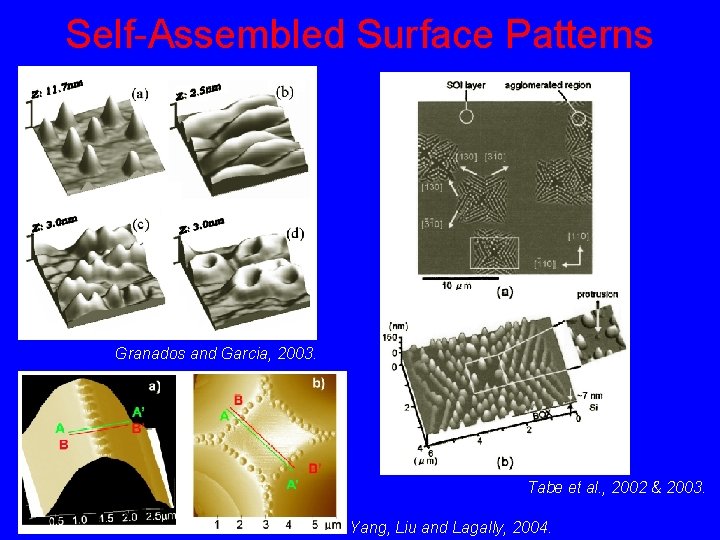
Self-Assembled Surface Patterns Granados and Garcia, 2003. Tabe et al. , 2002 & 2003. Yang, Liu and Lagally, 2004.

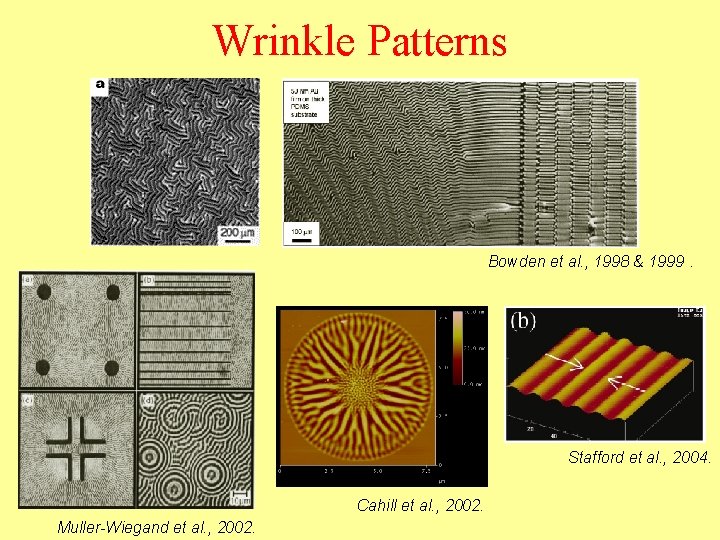
Wrinkle Patterns Bowden et al. , 1998 & 1999. Stafford et al. , 2004. Cahill et al. , 2002. Muller-Wiegand et al. , 2002.

Part I: Surface Diffusion-Controlled Patterns

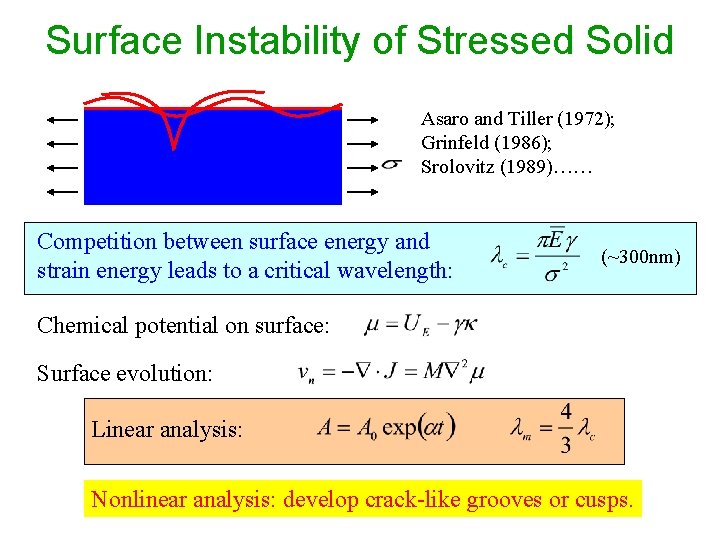
Surface Instability of Stressed Solid Asaro and Tiller (1972); Grinfeld (1986); Srolovitz (1989)…… Competition between surface energy and strain energy leads to a critical wavelength: (~300 nm) Chemical potential on surface: Surface evolution: Linear analysis: Nonlinear analysis: develop crack-like grooves or cusps.

Instability of Epitaxial Films Spencer, Voorhees and Davis (1991); Freund and Jonsdottir (1993); Gao (1993)…… The film is stressed due to lattice mismatch between the film and the substrate (e. g. , Ge on Si). Stress relaxation leads to formation of dislocations and/or surface roughening. Linear analysis: similar to that of stressed solids Nonlinear analysis: self-assembly of quantum dots How to control the size and order of quantum dots?

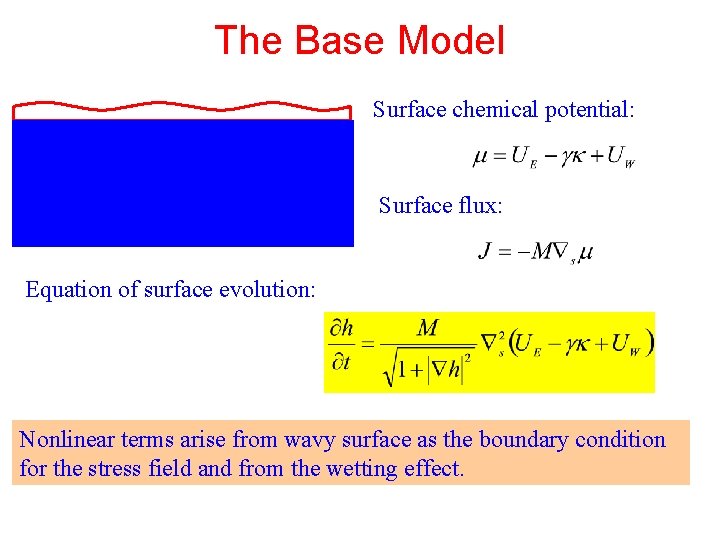
The Base Model Surface chemical potential: Surface flux: Equation of surface evolution: Nonlinear terms arise from wavy surface as the boundary condition for the stress field and from the wetting effect.

Stress Analysis Boundary condition on the surface: (In the order of Zeroth-order: First-order: (B. C. ) )

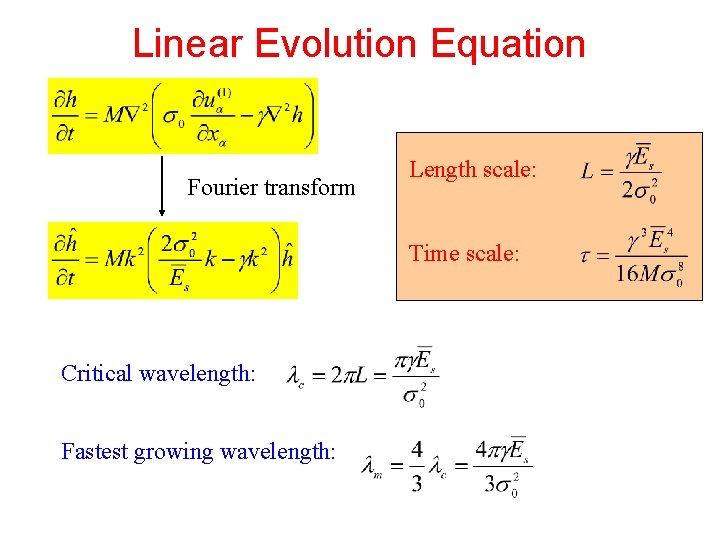
Linear Evolution Equation Fourier transform Length scale: Time scale: Critical wavelength: Fastest growing wavelength:

Nonlinear Stresses Second-order: (B. C. ) Nonlinear evolution equation:

Spectral Method Fourier transform of the nonlinear equation: Semi-implicit integration: Numerical simulations: Calculate spatial differentiation in the Fourier space Calculate nonlinear terms in the physical space Communicate between physical and Fourier spaces via FFT and its inverse

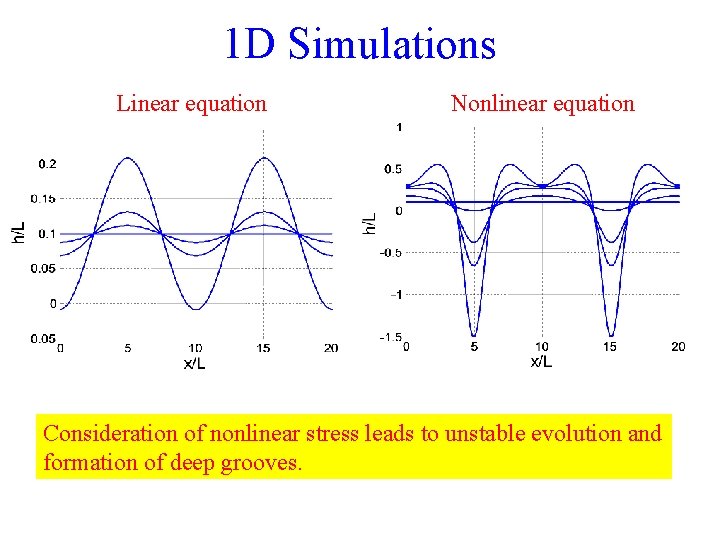
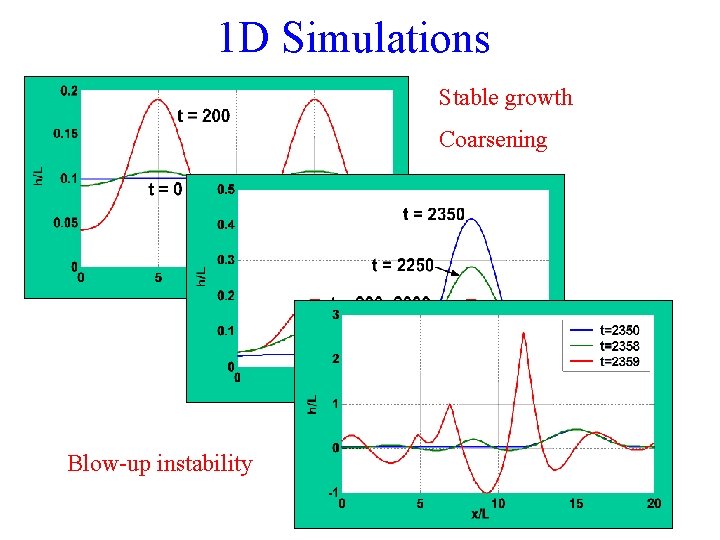
1 D Simulations Linear equation Nonlinear equation Consideration of nonlinear stress leads to unstable evolution and formation of deep grooves.

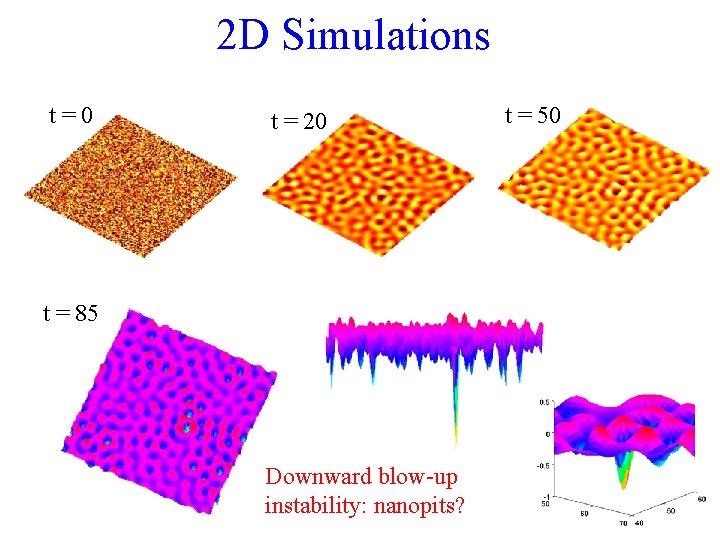
2 D Simulations t=0 t = 20 t = 85 Downward blow-up instability: nanopits? t = 50

Effect of Wetting Transition of surface energy (Spencer, 1999): Linear evolution equation with wetting:

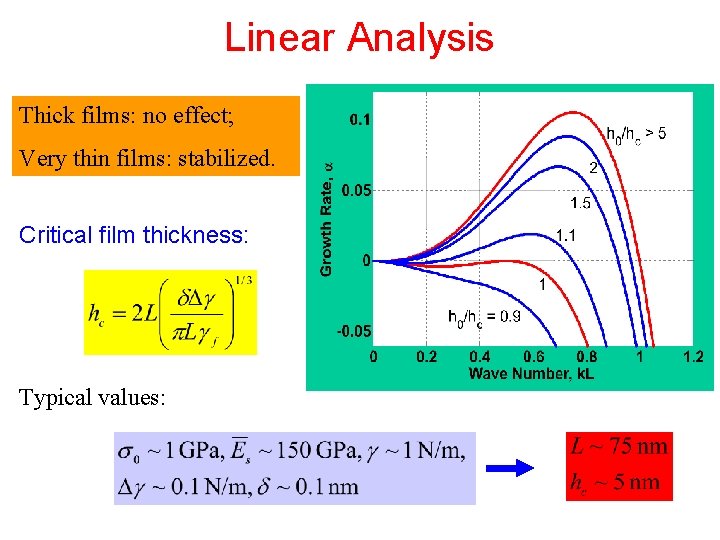
Linear Analysis Thick films: no effect; Very thin films: stabilized. Critical film thickness: Typical values:

1 D Simulations Stable growth Coarsening Blow-up instability

2 D Simulations t=0 t = 259 t = 50 t = 200 t = 260 Upward blow-up instability: nano whiskers?

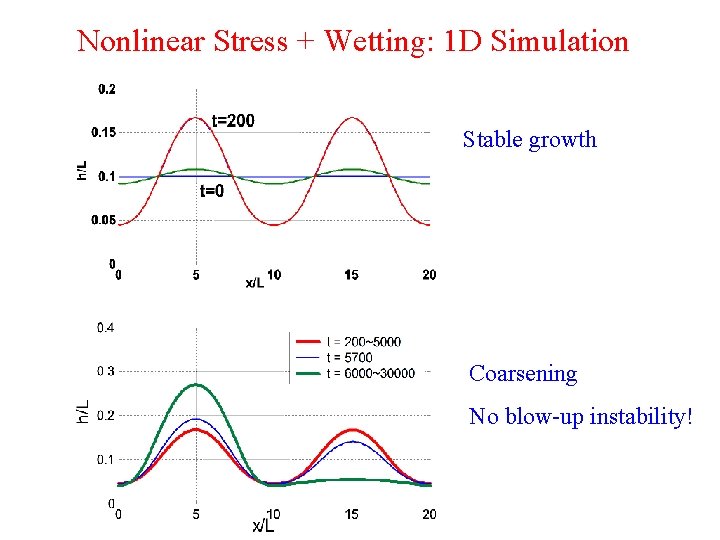
Nonlinear Stress + Wetting: 1 D Simulation Stable growth Coarsening No blow-up instability!

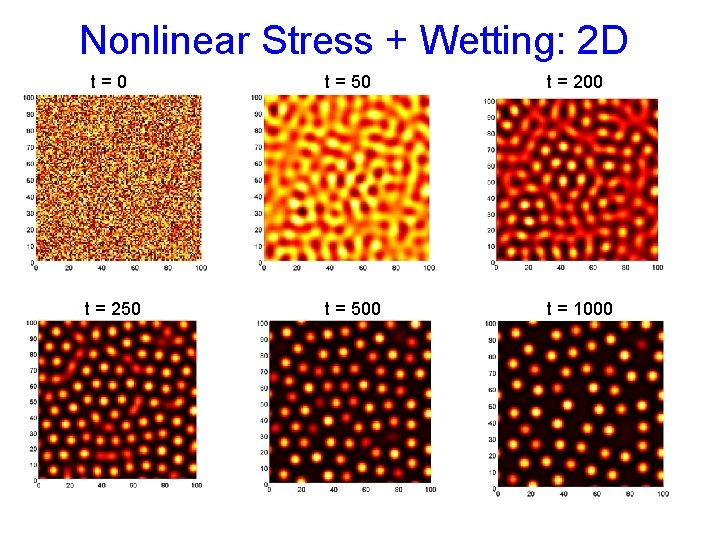
Nonlinear Stress + Wetting: 2 D t=0 t = 50 t = 200 t = 250 t = 500 t = 1000

Part I: Summary Nonlinear analysis of surface diffusion-controlled pattern evolution in strained epitaxial films: • Nonlinear stress field leads to downward blowup instability. • Wetting effect leads to upward blowup instability. • Combination of nonlinear stress and wetting stabilizes the evolution.

Part II: Compression-Induced Wrinkle Patterns

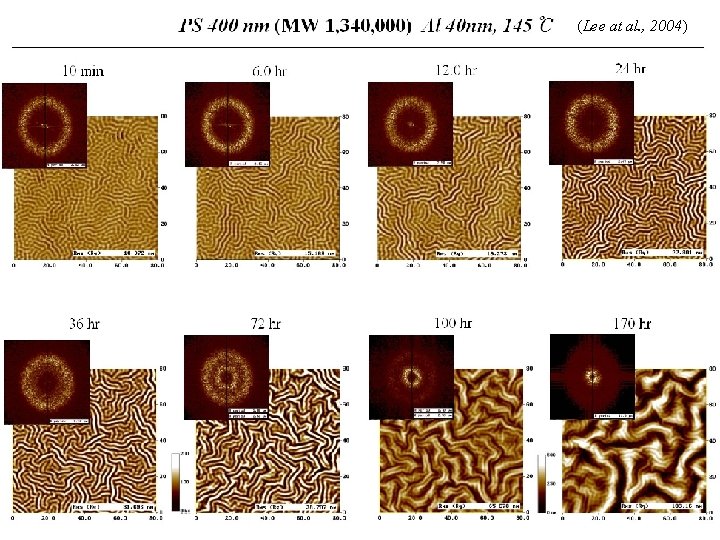
(Lee at al. , 2004)

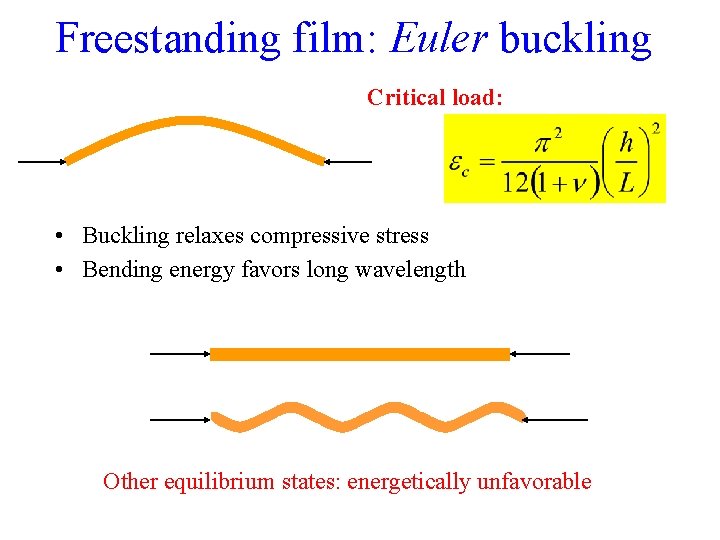
Freestanding film: Euler buckling Critical load: • Buckling relaxes compressive stress • Bending energy favors long wavelength Other equilibrium states: energetically unfavorable

On elastic substrates Elastic substrate • Deformation of the substrate disfavors wrinkling of long wavelengths and competes with bending to select an intermediate wavelength Wrinkling: short wavelength, on soft substrates, no delamination Buckling: long wavelength, on hard substrates, with delamination

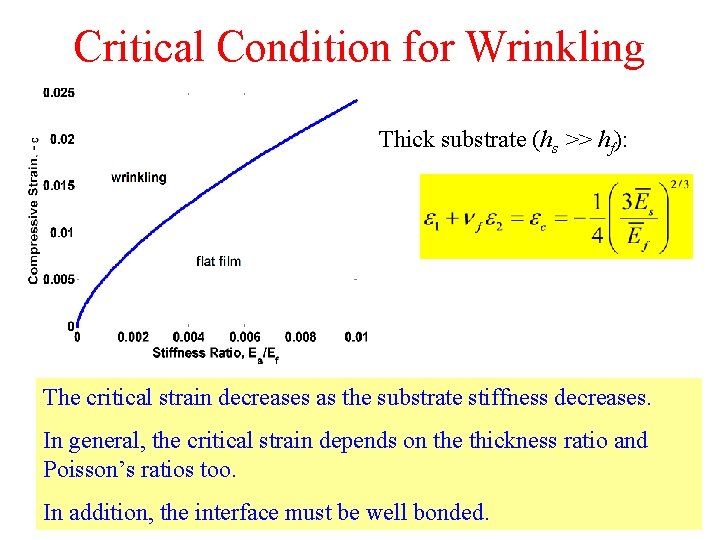
Critical Condition for Wrinkling Thick substrate (hs >> hf): The critical strain decreases as the substrate stiffness decreases. In general, the critical strain depends on the thickness ratio and Poisson’s ratios too. In addition, the interface must be well bonded.

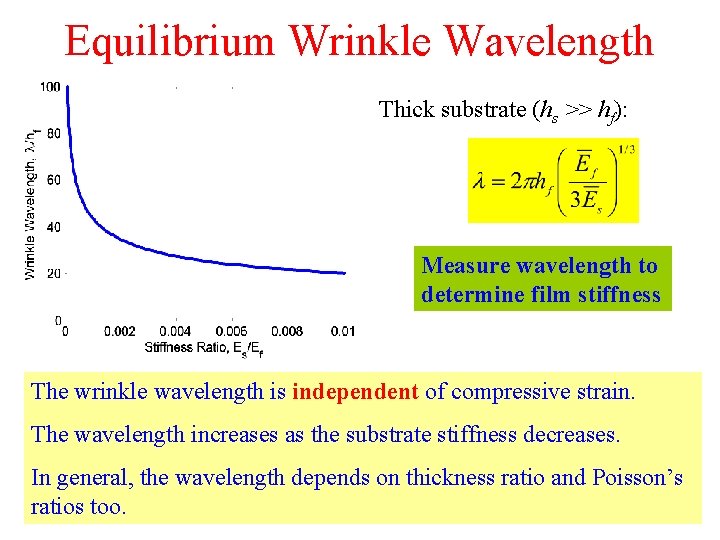
Equilibrium Wrinkle Wavelength Thick substrate (hs >> hf): Measure wavelength to determine film stiffness The wrinkle wavelength is independent of compressive strain. The wavelength increases as the substrate stiffness decreases. In general, the wavelength depends on thickness ratio and Poisson’s ratios too.

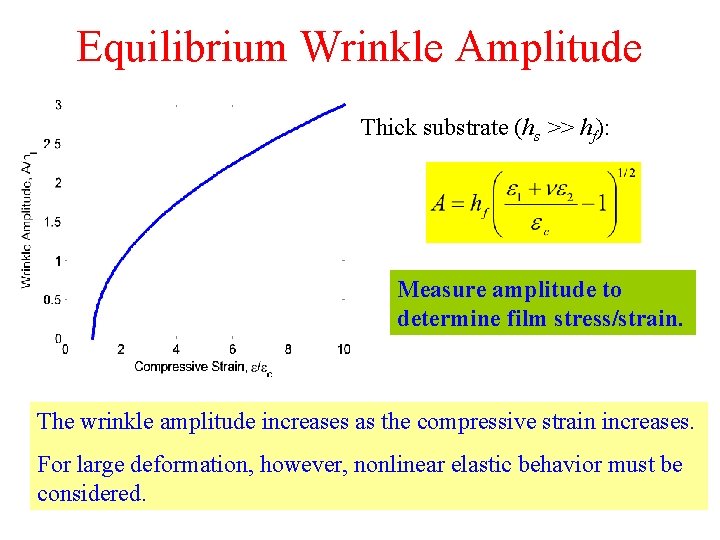
Equilibrium Wrinkle Amplitude Thick substrate (hs >> hf): Measure amplitude to determine film stress/strain. The wrinkle amplitude increases as the compressive strain increases. For large deformation, however, nonlinear elastic behavior must be considered.

Equilibrium Wrinkle Patterns In an elastic system, the equilibrium state minimizes the total strain energy. However, it is extremely difficult to find such a state for large film areas. More practically, one compares the energy of several possible patterns to determine the preferred pattern. How does the pattern emerge? How to control wrinkle patterns?

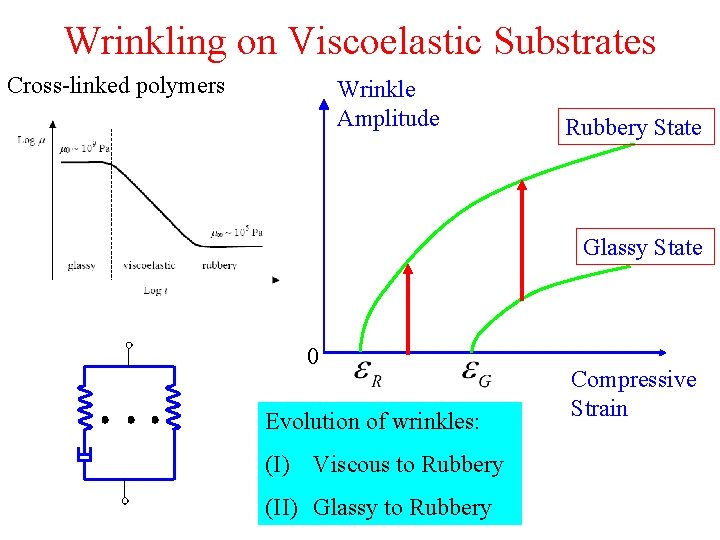
Wrinkling on Viscoelastic Substrates Cross-linked polymers Wrinkle Amplitude Rubbery State Glassy State 0 Evolution of wrinkles: (I) Viscous to Rubbery (II) Glassy to Rubbery Compressive Strain

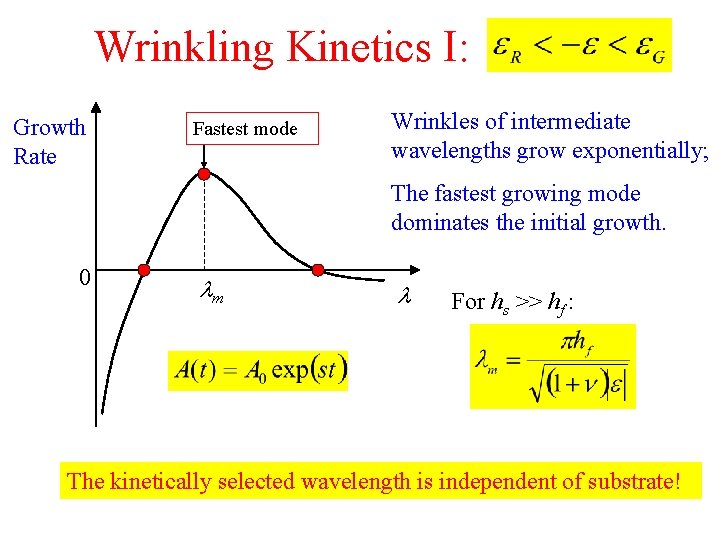
Wrinkling Kinetics I: Growth Rate Fastest mode Wrinkles of intermediate wavelengths grow exponentially; The fastest growing mode dominates the initial growth. 0 m For hs >> hf : The kinetically selected wavelength is independent of substrate!

Wrinkling Kinetics II: Instantaneous wrinkle at the glassy state: Kinetic growth at the initial stage: Long-term evolution:

Evolution Equations

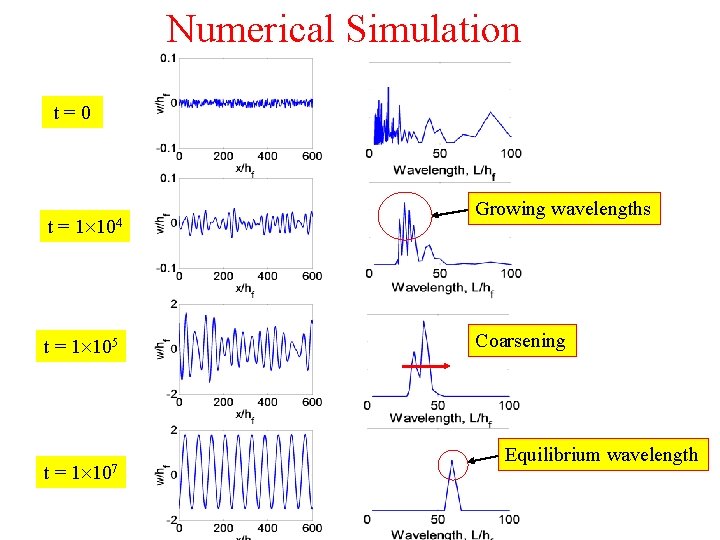
Numerical Simulation t=0 t= 1 104 t = 1 105 t= 1 107 Growing wavelengths Coarsening Equilibrium wavelength

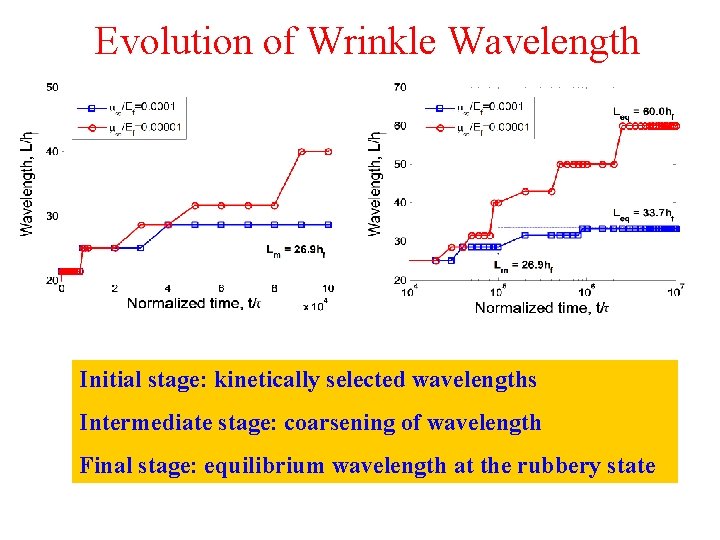
Evolution of Wrinkle Wavelength Initial stage: kinetically selected wavelengths Intermediate stage: coarsening of wavelength Final stage: equilibrium wavelength at the rubbery state

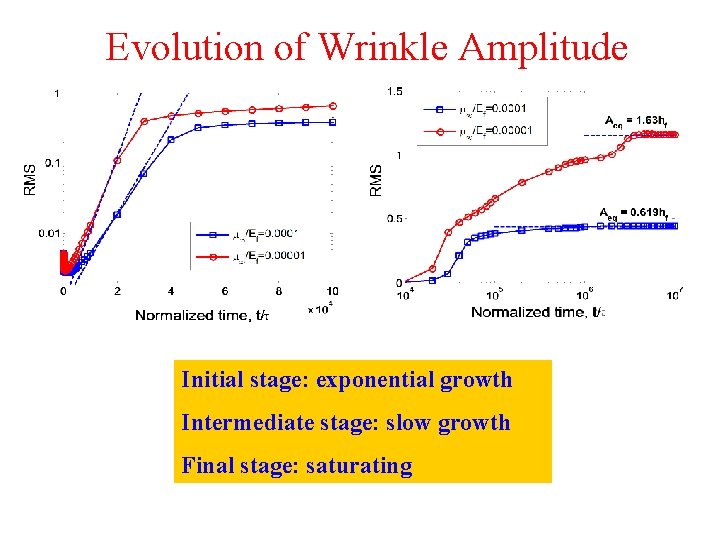
Evolution of Wrinkle Amplitude Initial stage: exponential growth Intermediate stage: slow growth Final stage: saturating

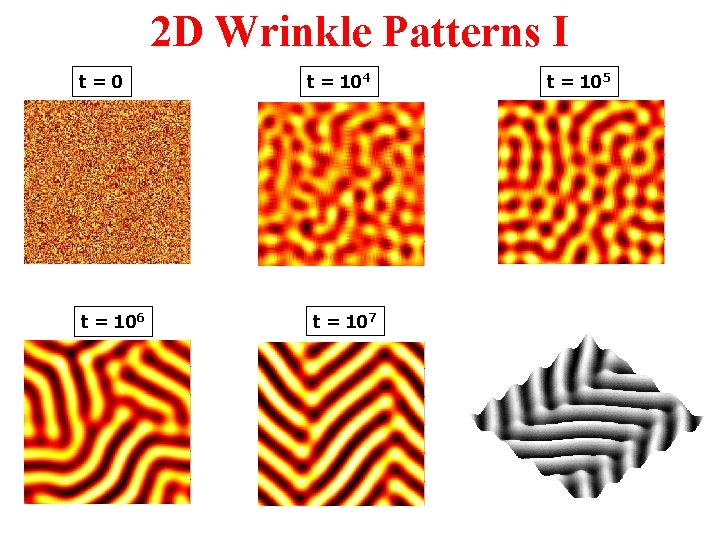
2 D Wrinkle Patterns I t=0 t = 106 t = 104 t = 107 t = 105

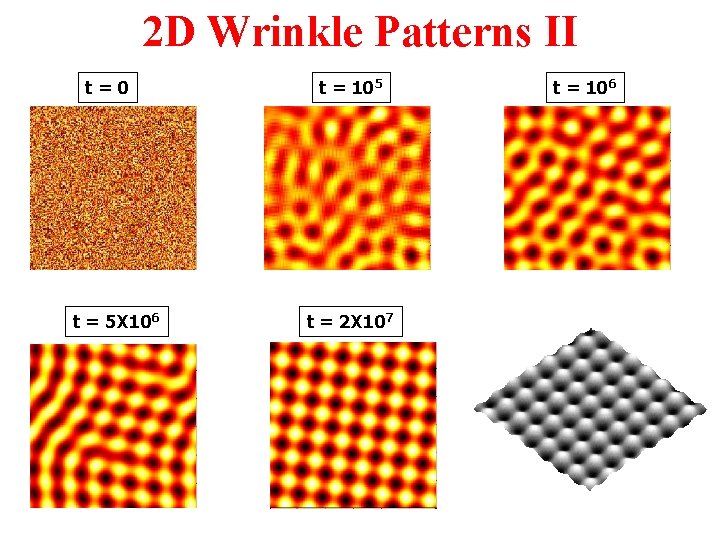
2 D Wrinkle Patterns II t=0 t = 5 X 106 t = 105 t = 2 X 107 t = 106

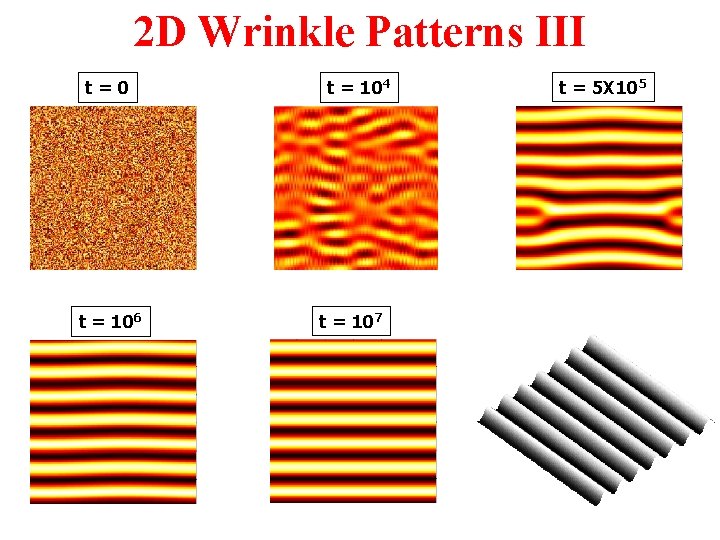
2 D Wrinkle Patterns III t=0 t = 106 t = 104 t = 107 t = 5 X 105

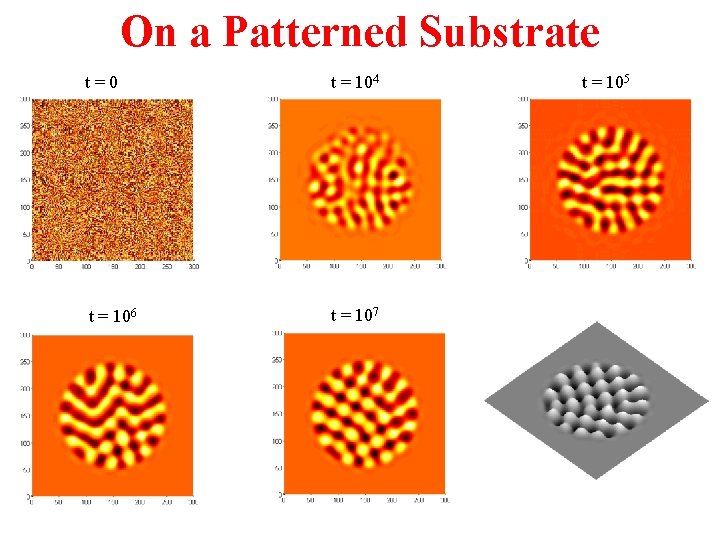
On a Patterned Substrate t=0 t = 104 t = 106 t = 107 t = 105

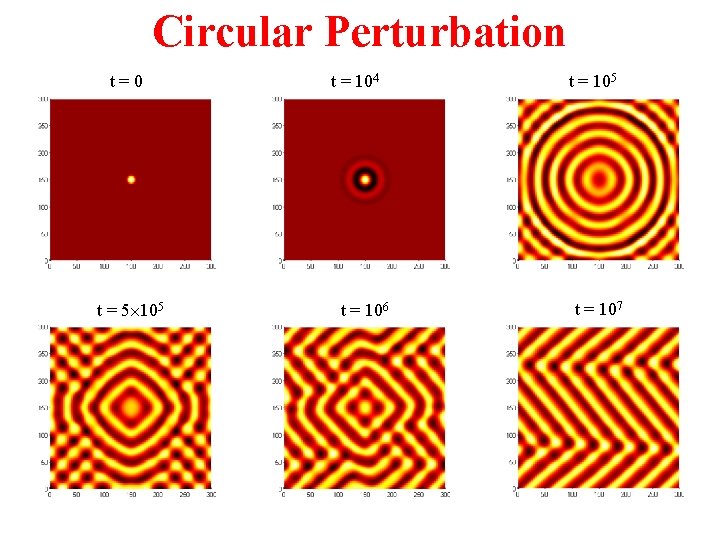
Circular Perturbation t=0 t = 5 105 t = 104 t = 106 t = 105 t = 107

Evolution of Wrinkle Patterns • Symmetry breaking in isotropic system: – from spherical caps to elongated ridges – from labyrinth to herringbone. • Symmetry breaking due to anisotropic strain – from labyrinth to parallel stripes • Controlling the wrinkle patterns – On patterned substrates – By introducing initial defects

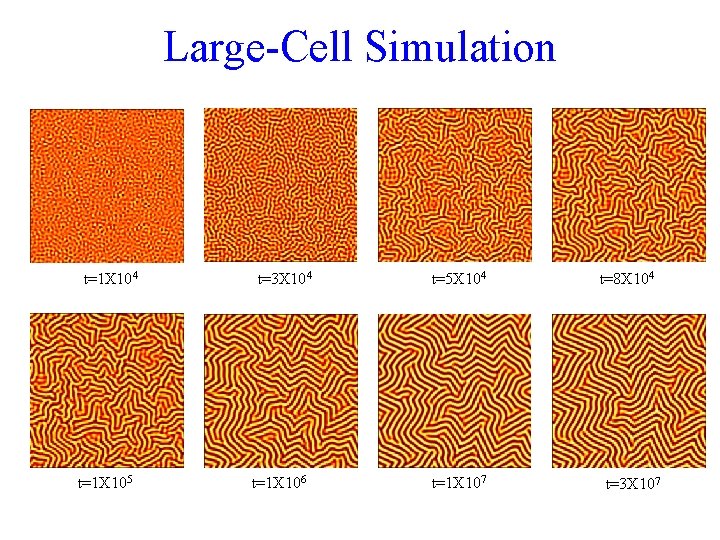
Large-Cell Simulation t=1 X 104 t=1 X 105 t=3 X 104 t=1 X 106 t=5 X 104 t=1 X 107 t=8 X 104 t=3 X 107

Acknowledgments • Co-workers: Se Hyuk Im, Yaoyu Pang, Hai Liu, S. K. Banerjee, H. H. Lee, C. M. Stafford • Funding: NSF, ATP, Texas AMRC Thank you !