Dynamics of Realworld Networks Jure Leskovec Machine Learning

Dynamics of Real-world Networks Jure Leskovec Machine Learning Department Carnegie Mellon University jure@cs. cmu. edu http: //www. cs. cmu. edu/~jure 1

Committee members n n Christos Faloutsos Avrim Blum Jon Kleinberg John Lafferty 2

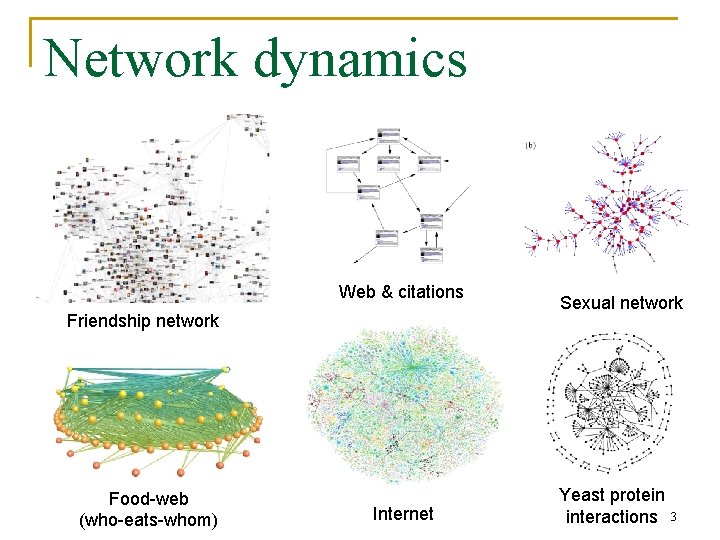
Network dynamics Web & citations Friendship network Food-web (who-eats-whom) Internet Sexual network Yeast protein interactions 3

Large real world networks n Instant messenger network q q n N = 180 million nodes E = 1. 3 billion edges Blog network q N = 2. 5 million nodes E = 5 million edges Autonomous systems q q n Citation network of physics papers q q n N = 31, 000 nodes E = 350, 000 edges Recommendation network q q N = 3 million nodes E = 16 million edges N = 6, 500 nodes E = 26, 500 edges 4

Questions we ask n n Do networks follow patterns as they grow? How to generate realistic graphs? How does influence spread over the network (chains, stars)? How to find/select nodes to detect cascades? 5

Our work: Network dynamics n Our research focuses on analyzing and modeling the structure, evolution and dynamics of large real-world networks q Evolution n q Growth and evolution of networks Cascades n Processes taking place on networks 6

Our work: Goals n 3 parts / goals q G 1: What are interesting statistical properties of network structure? n q G 2: What is a good tractable model? n q e. g. , 6 -degrees e. g. , preferential attachment G 3: Use models and findings to predict future behavior n e. g. , node immunization 7

Our work: Overview S 1: Dynamics of network evolution S 2: Dynamics of processes on networks G 1: Patterns G 2: Models G 3: Predictions 8

Our work: Overview S 1: Dynamics of network evolution S 2: Dynamics of processes on networks G 1: Patterns KDD ‘ 05 TKDD ’ 07 PKDD ‘ 06 ACM EC ’ 06 G 2: Models KDD ‘ 05 PAKDD ’ 05 SDM ‘ 07 TWEB ’ 07 KDD ‘ 06 ICML ’ 07 WWW ‘ 07 submission to KDD G 3: Predictions 9

Our work: Impact and applications n Structural properties q n Graph models q q q n Abnormality detection Graph generation Graph sampling and extrapolations Anonymization Cascades q q Node selection and targeting Outbreak detection 10

Outline n n Introduction Completed work q q n Proposed work q q q n S 1: Network structure and evolution S 2: Network cascades Kronecker time evolving graphs Large online communication networks Links and information cascades Conclusion 11

Completed work: Overview S 1: Dynamics of network evolution S 2: Dynamics of processes on networks G 1: Patterns Densification Shrinking diameters Cascade shape and size G 2: Models Forest Fire Kronecker graphs Cascade generation model Estimating Kronecker parameters Selecting nodes for detecting cascades G 3: Predictions 12

Completed work: Overview S 1: Dynamics of network evolution S 2: Dynamics of processes on networks G 1: Patterns Densification Shrinking diameters Cascade shape and size G 2: Models Forest Fire Kronecker graphs Cascade generation model Estimating Kronecker parameters Selecting nodes for detecting cascades G 3: Predictions 13

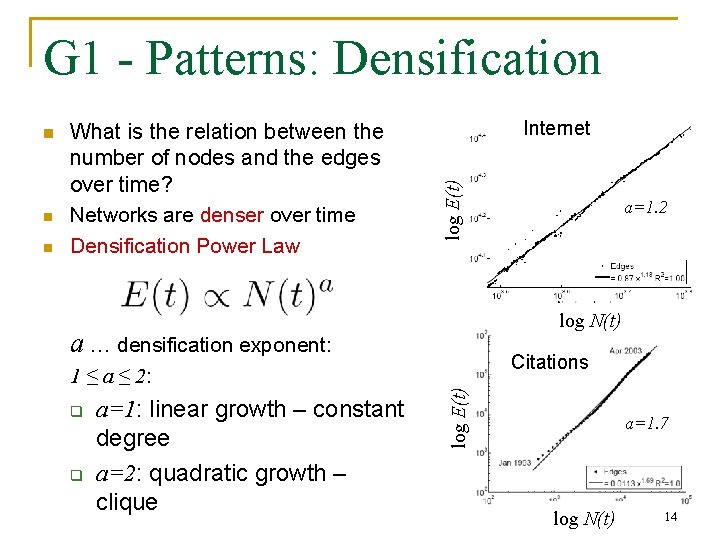
G 1 - Patterns: Densification n Internet log E(t) n What is the relation between the number of nodes and the edges over time? Networks are denser over time Densification Power Law log N(t) a … densification exponent: 1 ≤ a ≤ 2: q q a=1: linear growth – constant degree a=2: quadratic growth – clique a=1. 2 Citations log E(t) n a=1. 7 log N(t) 14

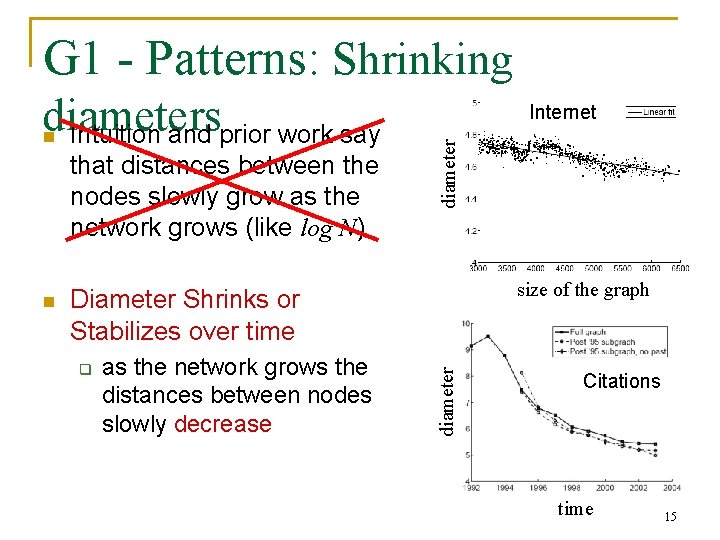
G 1 - Patterns: Shrinking n that distances between the nodes slowly grow as the network grows (like log N) size of the graph Diameter Shrinks or Stabilizes over time q as the network grows the distances between nodes slowly decrease diameter n Internet diameters Intuition and prior work say Citations time 15

G 2 - Models: Kronecker graphs n Want to have a model that can generate a realistic graph with realistic growth q q n Patterns for static networks Patterns for evolving networks The model should be q analytically tractable n q We can prove properties of graphs the model generates computationally tractable n We can estimate parameters 16

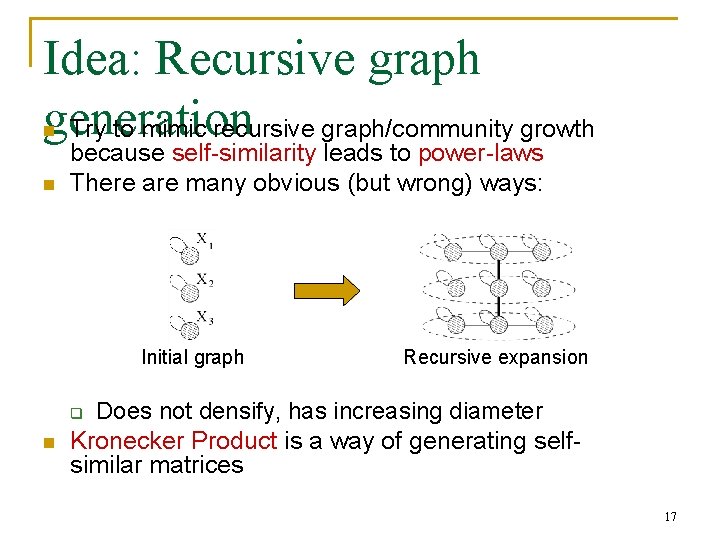
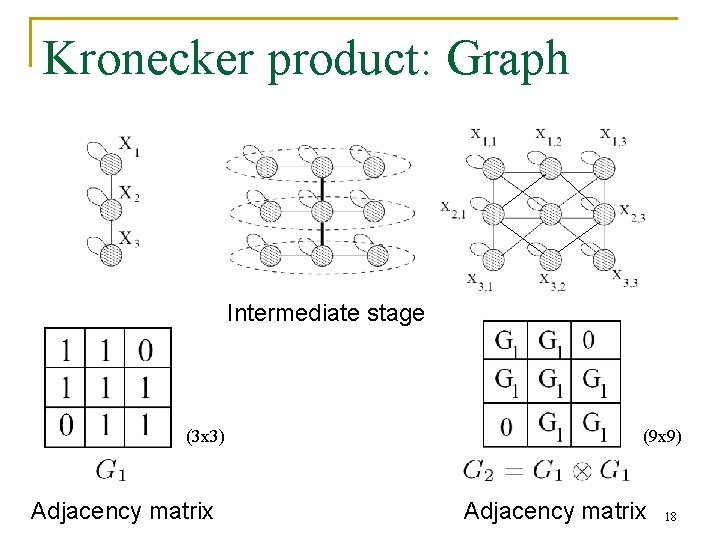
Idea: Recursive graph generation Try to mimic recursive graph/community growth n n because self-similarity leads to power-laws There are many obvious (but wrong) ways: Initial graph Recursive expansion Does not densify, has increasing diameter Kronecker Product is a way of generating selfsimilar matrices q n 17

Kronecker product: Graph Intermediate stage (3 x 3) Adjacency matrix (9 x 9) Adjacency matrix 18

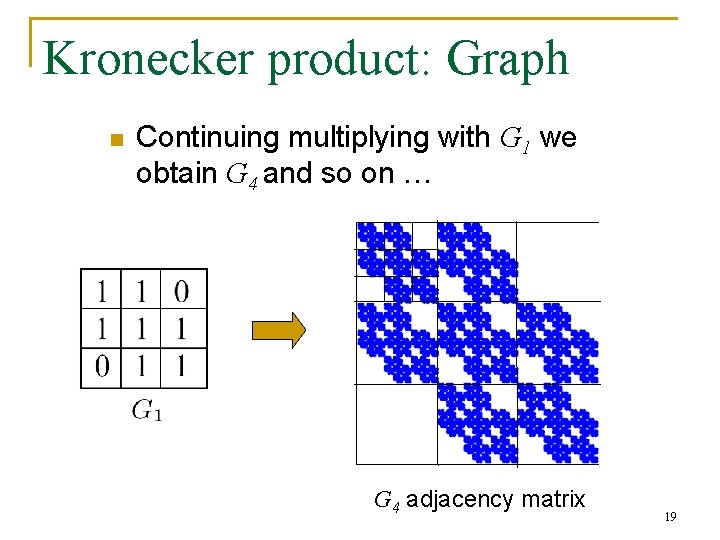
Kronecker product: Graph n Continuing multiplying with G 1 we obtain G 4 and so on … G 4 adjacency matrix 19

Properties of Kronecker graphs n We show that Kronecker multiplication generates graphs that have: q Properties of static networks Power Law Degree Distribution Power Law eigenvalue and eigenvector distribution Small Diameter q Properties of dynamic networks Densification Power Law Shrinking / Stabilizing Diameter n n This means “shapes” of the distributions match but the properties are not independent How do we set the initiator to match the real graph? 20

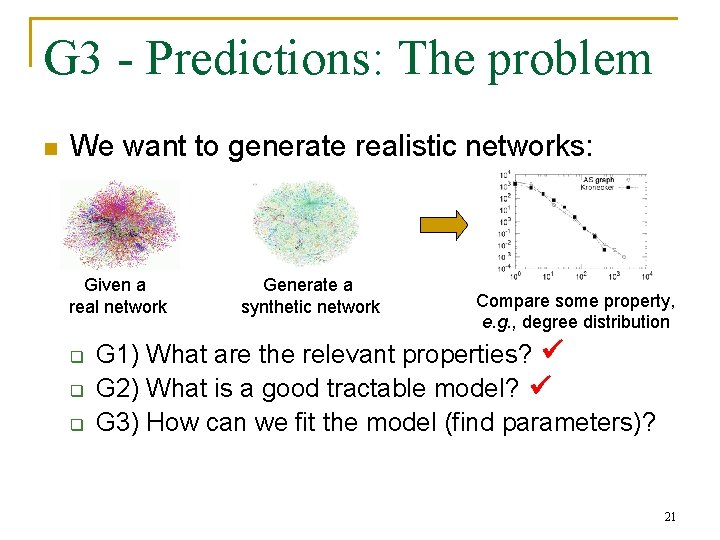
G 3 - Predictions: The problem n We want to generate realistic networks: Given a real network q q q Generate a synthetic network Compare some property, e. g. , degree distribution G 1) What are the relevant properties? G 2) What is a good tractable model? G 3) How can we fit the model (find parameters)? 21

Model estimation: approach n Maximum likelihood estimation q q Given real graph G Estimate the Kronecker initiator graph Θ (e. g. , 3 x 3 ) which n We need to (efficiently) calculate n And maximize over Θ 22

Model estimation: solution n Naïvely estimating the Kronecker initiator takes O(N!N 2) time: q N! for graph isomorphism n q N 2 for traversing the graph adjacency matrix n n Metropolis sampling: N! (big) const Properties of Kronecker product and sparsity << N 2): N 2 E (E We can estimate the parameters in linear time O(E) 23

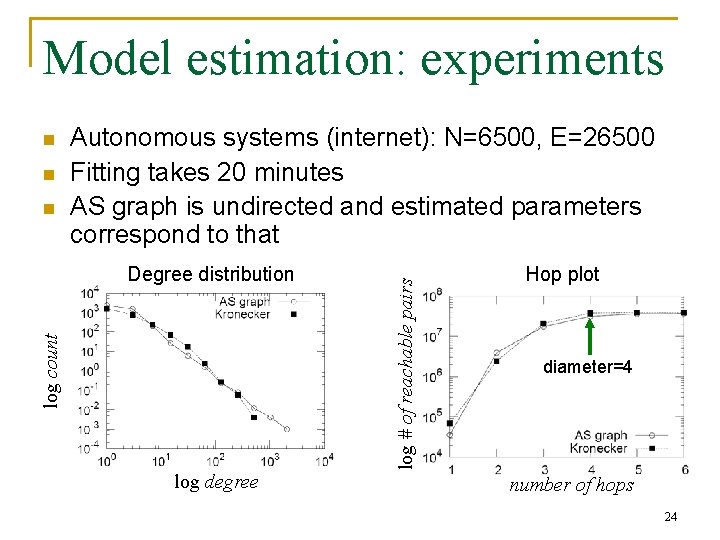
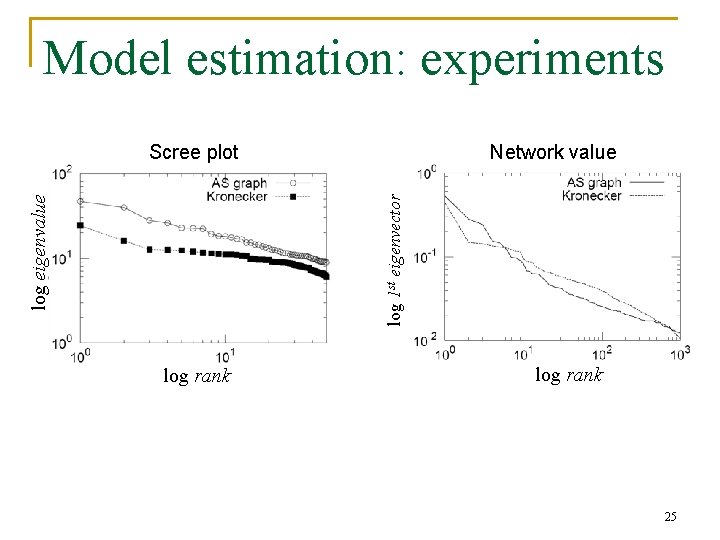
Model estimation: experiments n n Autonomous systems (internet): N=6500, E=26500 Fitting takes 20 minutes AS graph is undirected and estimated parameters correspond to that log count Degree distribution log degree log # of reachable pairs n Hop plot diameter=4 number of hops 24

Model estimation: experiments Network value log eigenvalue log 1 st eigenvector Scree plot log rank 25

Completed work: Overview S 1: Dynamics of network evolution S 2: Dynamics of processes on networks G 1: Patterns Densification Shrinking diameters Cascade shape and size G 2: Models Forest Fire Kronecker graphs Cascade generation model Estimating Kronecker parameters Selecting nodes for detecting cascades G 3: Predictions 26

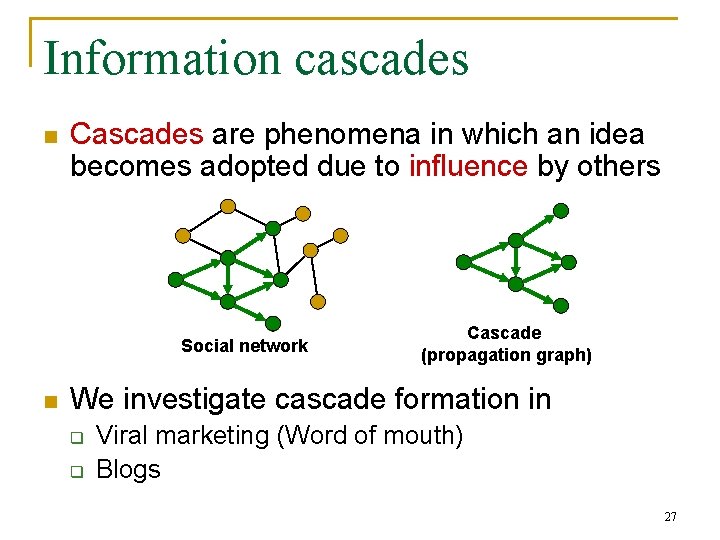
Information cascades n Cascades are phenomena in which an idea becomes adopted due to influence by others Social network n Cascade (propagation graph) We investigate cascade formation in q q Viral marketing (Word of mouth) Blogs 27

Cascades: Questions n n n What kinds of cascades arise frequently in real life? Are they like trees, stars, or something else? What is the distribution of cascade sizes (exponential tail / heavy-tailed)? When is a person going to follow a recommendation? 28

Cascades in viral marketing n Senders and followers of recommendations receive discounts on products 10% credit n n 10% off Recommendations are made at time of purchase Data: 3 million people, 16 million recommendations, 500 k products (books, DVDs, videos, music) 29

Product recommendation network purchase following a recommendation customer recommending a product customer not buying a recommended product 30

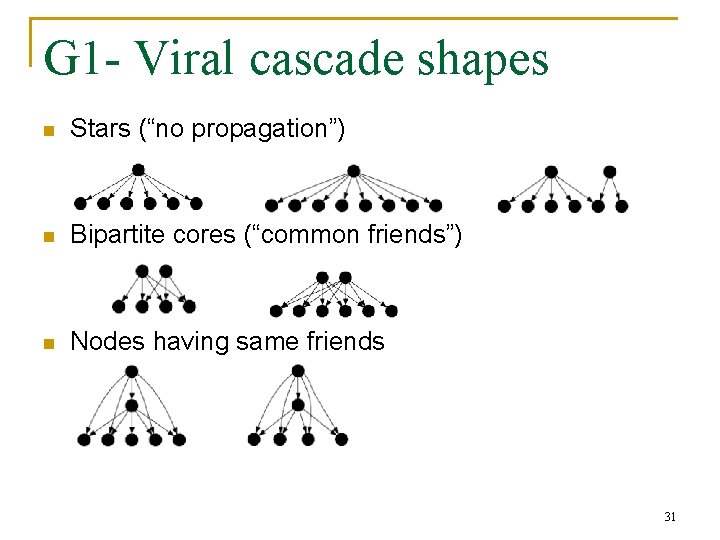
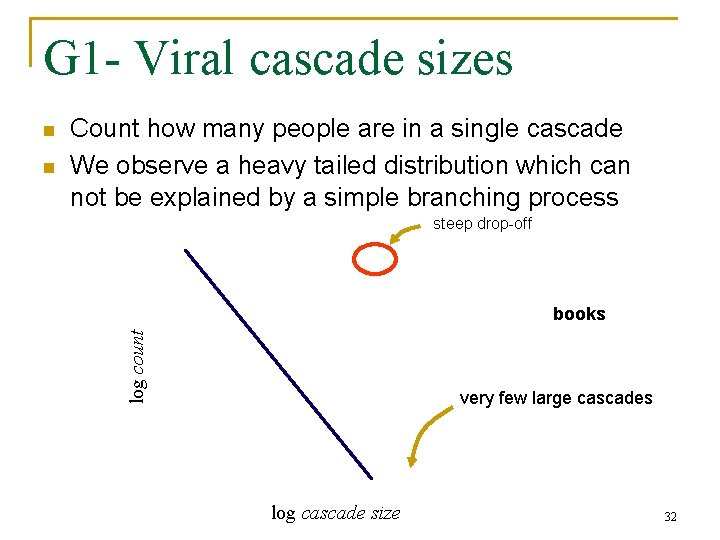
G 1 - Viral cascade shapes n Stars (“no propagation”) n Bipartite cores (“common friends”) n Nodes having same friends 31

G 1 - Viral cascade sizes n Count how many people are in a single cascade We observe a heavy tailed distribution which can not be explained by a simple branching process steep drop-off books log count n very few large cascades log cascade size 32

Does receiving more recommendations increase the likelihood of buying? BOOKS DVDs 33

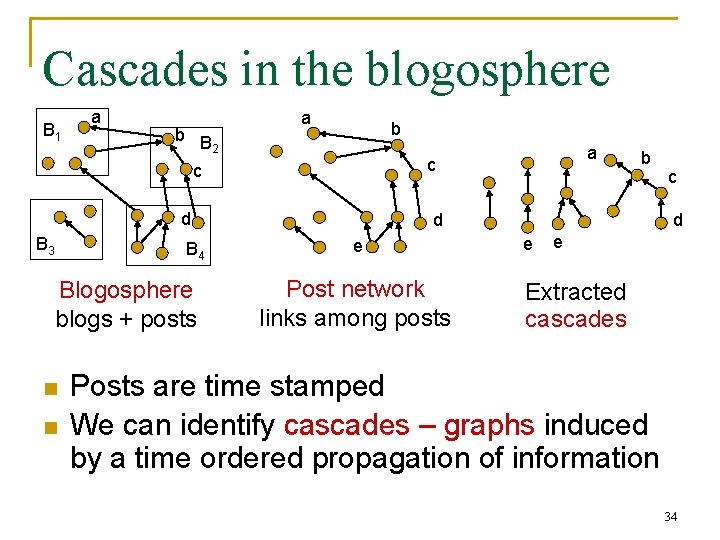
Cascades in the blogosphere B 1 a b B 2 a b c d B 3 B 4 Blogosphere blogs + posts n n a c b d e Post network links among posts c d e e Extracted cascades Posts are time stamped We can identify cascades – graphs induced by a time ordered propagation of information 34

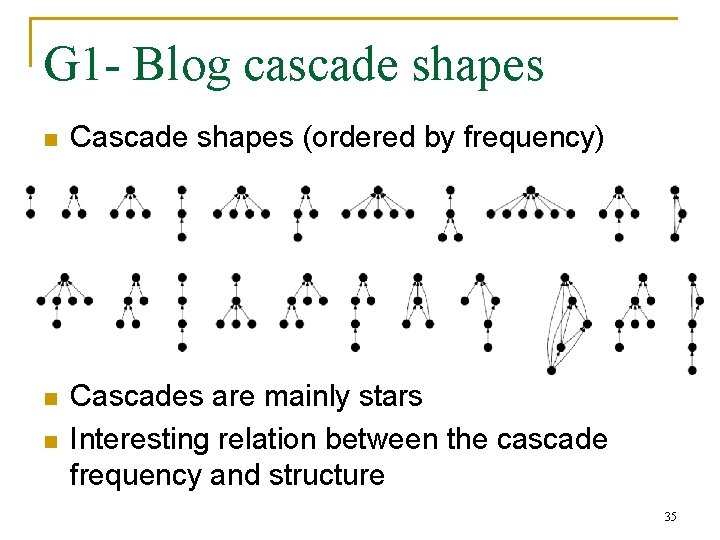
G 1 - Blog cascade shapes n Cascade shapes (ordered by frequency) n Cascades are mainly stars Interesting relation between the cascade frequency and structure n 35

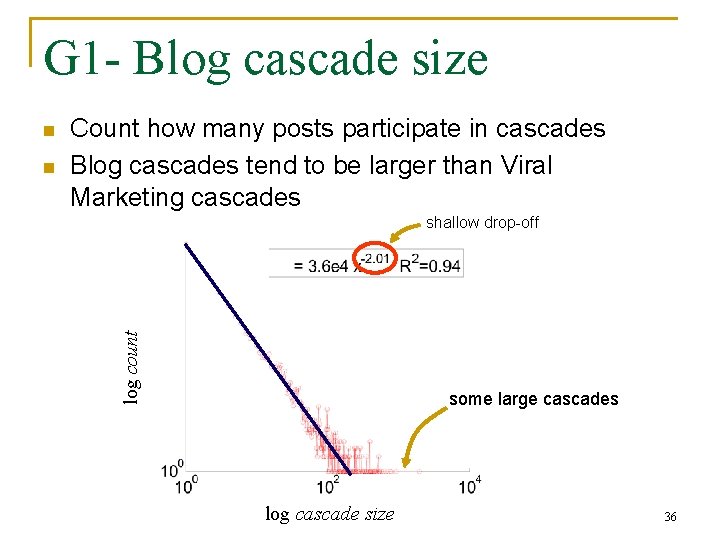
G 1 - Blog cascade size n Count how many posts participate in cascades Blog cascades tend to be larger than Viral Marketing cascades shallow drop-off log count n some large cascades log cascade size 36

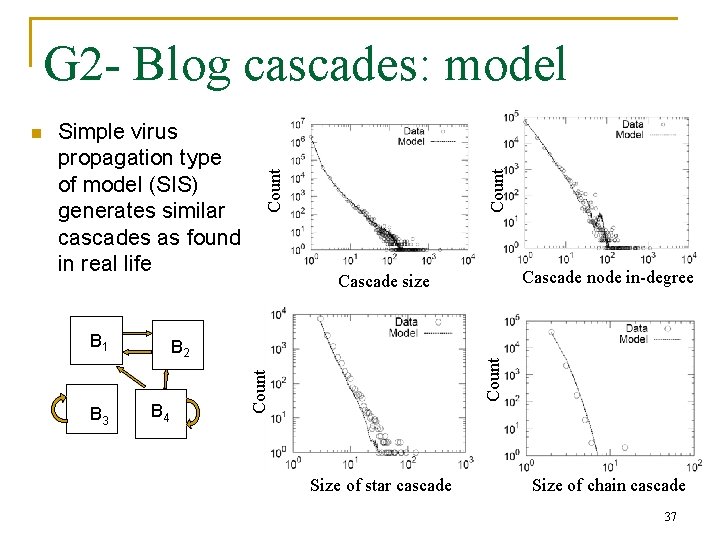
B 1 B 3 Count Simple virus propagation type of model (SIS) generates similar cascades as found in real life Count B 2 B 4 Cascade node in-degree Cascade size Count n Count G 2 - Blog cascades: model Size of star cascade Size of chain cascade 37

G 3 - Node selection for cascade detection n n Observing cascades we want to select a set of nodes to quickly detect cascades Given a limited budget of attention/sensors q q Which blogs should one read to be most up to date? Where should we position monitoring stations to quickly detect disease outbreaks? 38

Node selection: algorithm n n Node selection is NP hard We exploit submodularity of objective functions to q q develop scalable node selection algorithms give performance guarantees Solution quality Worst case bound Our solution Number of blogs n In practice our solution is at most 5 -15% from optimal 39

Outline n n Introduction Completed work q q n Proposed work q q q n Network structure and evolution Network cascades Large communication networks Links and information cascades Kronecker time evolving graphs Conclusion 40

Proposed work: Overview S 2: Dynamics of processes on networks S 1: Dynamics of network evolution Dynamics in 1 communication networks G 1: Patterns G 2: Models G 3: Predictions 2 3 Models of link and cascade creation Kronecker time evolving graphs 41

1 Proposed work: Communication networks n Large communication network q n 1 billion conversations per day, 3 TB of data! How communication and network properties change with user demographics (age, location, sex, distance) q q Test 6 degrees of separation Examine transitivity in the network 42

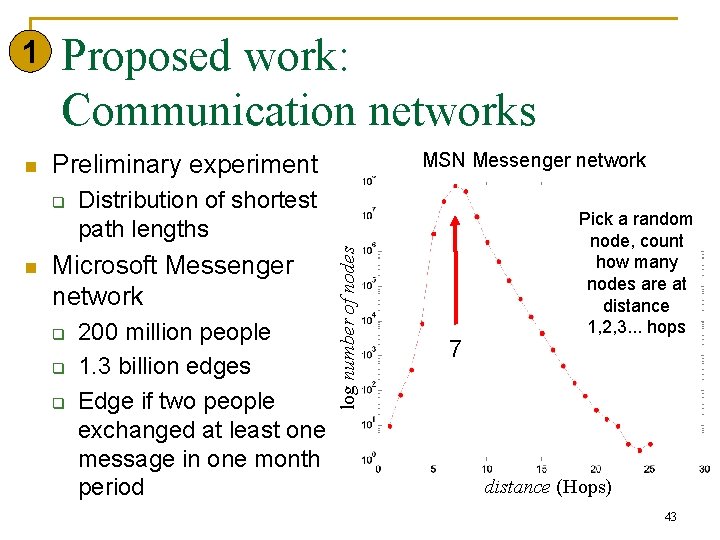
n Proposed work: Communication networks q n MSN Messenger network Preliminary experiment Distribution of shortest path lengths Microsoft Messenger network q q q 200 million people 1. 3 billion edges Edge if two people exchanged at least one message in one month period log number of nodes 1 7 Pick a random node, count how many nodes are at distance 1, 2, 3. . . hops distance (Hops) 43

2 Proposed work: Links & cascades n n Given labeled nodes, how do links and cascades form? Propagation of information q n Do blogs have particular cascading properties? Propagation of trust q Social network of professional acquaintances n n q q 7 million people, 50 million edges Rich temporal and network information How do various factors (profession, education, location) influence link creation? How do invitations propagate? 44

Proposed work: Kronecker graphs 3 n Graphs with weighted edges q n Move beyond Bernoulli edge generation model Algorithms for estimating parameters of time evolving networks q Allow parameters to slowly evolve over time Θt Θt+1 Θt+2 45

Timeline n n n May ‘ 07 1 communication network q Jun – Aug ‘ 07 q research on on-line time evolving networks Sept– Dec ‘ 07 2 Cascade formation and link prediction q Jan – Apr ’ 08 3 Kronecker time evolving graphs q Apr – May ‘ 08 q Write thesis Jun ‘ 08 q Thesis defense 46

References q q q q Graphs over Time: Densification Laws, Shrinking Diameters and Possible Explanations, by Jure Leskovec, Jon Kleinberg, Christos Faloutsos, ACM KDD 2005 Graph Evolution: Densification and Shrinking Diameters, by Jure Leskovec, Jon Kleinberg and Christos Faloutsos, ACM TKDD 2007 Realistic, Mathematically Tractable Graph Generation and Evolution, Using Kronecker Multiplication, by Jure Leskovec, Deepay Chakrabarti, Jon Kleinberg and Christos Faloutsos, PKDD 2005 Scalable Modeling of Real Graphs using Kronecker Multiplication, by Jure Leskovec and Christos Faloutsos, ICML 2007 The Dynamics of Viral Marketing, by Jure Leskovec, Lada Adamic, Bernado Huberman, ACM EC 2006 Cost-effective outbreak detection in networks, by Jure Leskovec, Andreas Krause, Carlos Guestrin, Christos Faloutsos, Jeanne Van. Briesen, Natalie Glance, in submission to KDD 2007 Cascading behavior in large blog graphs, by Jure Leskovec, Marry Mc. Glohon, Christos Faloutsos, Natalie Glance, Matthew Hurst, SIAM DM 2007 Acknowledgements: Christos Faloutsos, Mary Mc. Glohon, Jon Kleinberg, Zoubin Gharamani, Pall Melsted, Andreas Krause, Carlos Guestrin, Deepay Chakrabarti, Marko Grobelnik, Dunja Mladenic, Natasa Milic-Frayling, Lada Adamic, Bernardo Huberman, Eric Horvitz, Susan Dumais 47