Dynamics of Quantum Degenerate Gases at Finite Temperature

Dynamics of Quantum. Degenerate Gases at Finite Temperature Brian Jackson University of Trento, and INFM-BEC Inauguration meeting and Lev Pitaevskii’s Birthday: Trento, March 14 -15

In collaboration with: Eugene Zaremba (Queen’s University, Canada) Allan Griffin (University of Toronto, Canada) Jamie Williams (NIST, USA) Tetsuro Nikuni (Tokyo Univ. of Science, Japan) In Trento: Sandro Stringari Lev Pitaevskii Luciano Viverit

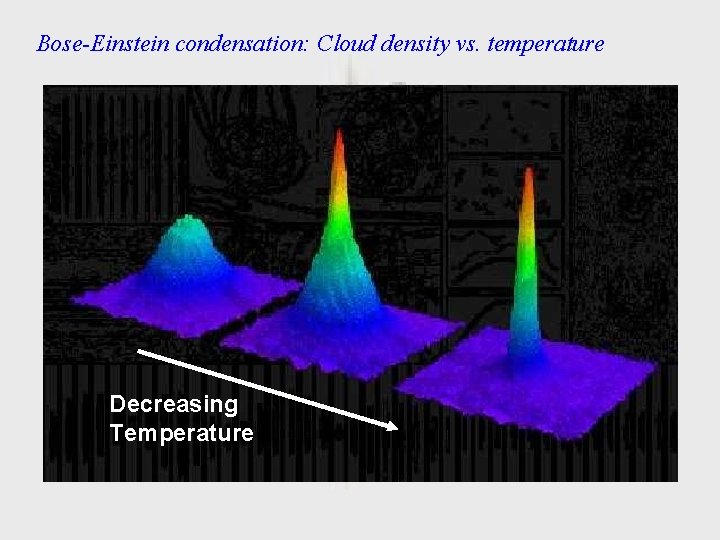
Bose-Einstein condensation: Cloud density vs. temperature Decreasing Temperature

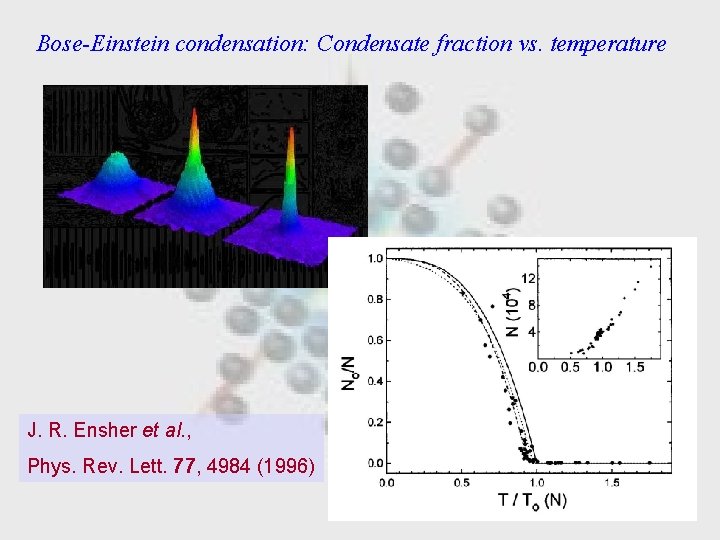
Bose-Einstein condensation: Condensate fraction vs. temperature J. R. Ensher et al. , Phys. Rev. Lett. 77, 4984 (1996)

Outline • • Bose-Einstein condensation at finite T • collective modes • ZNG theory and numerical methods • applications: scissors, quadrupole, and transverse breathing modes Normal Fermi gases • • Collective modes in the unitarity limit Summary

Collective modes: zero T Condensate confined in magnetic trap, which can be approximated with the harmonic form:

Collective modes: zero T Change trap frequency: condensate undergoes undamped collective oscillations

Collective modes: zero T Gross-Pitaevskii equation: a: s-wave scattering length m: atomic mass Normalization condition:

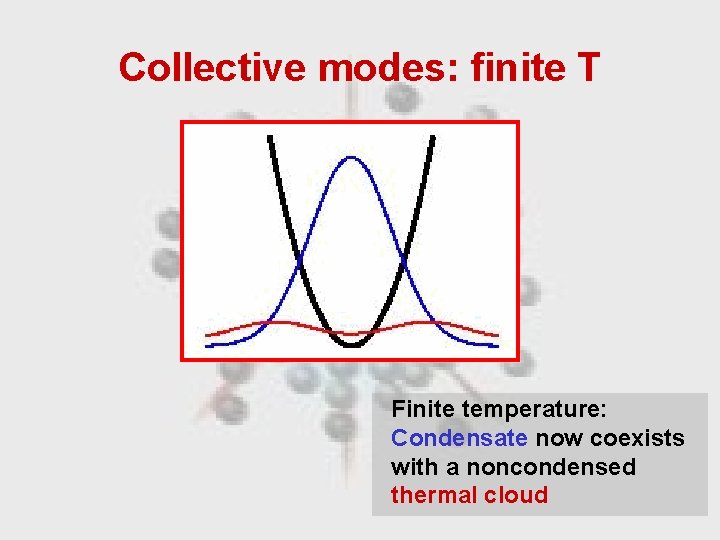
Collective modes: finite T Finite temperature: Condensate now coexists with a noncondensed thermal cloud

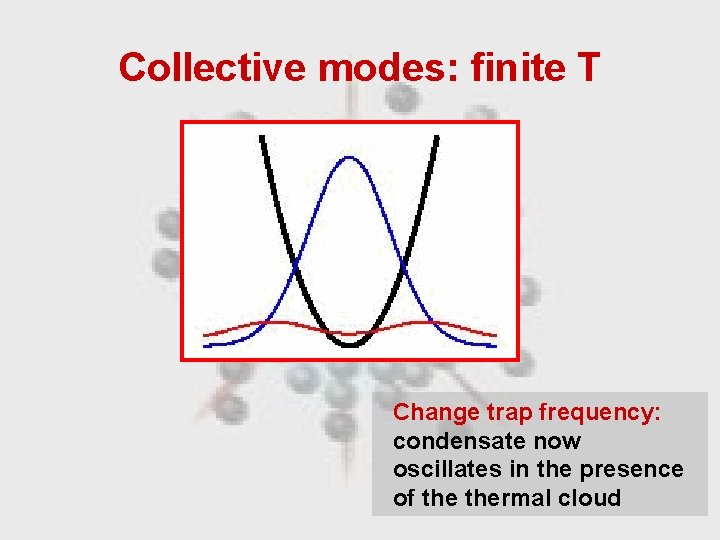
Collective modes: finite T Change trap frequency: condensate now oscillates in the presence of thermal cloud

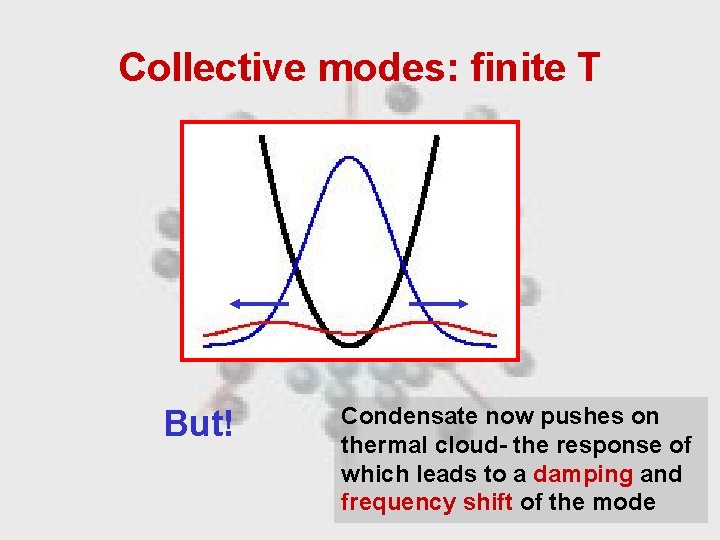
Collective modes: finite T But! Condensate now pushes on thermal cloud- the response of which leads to a damping and frequency shift of the mode

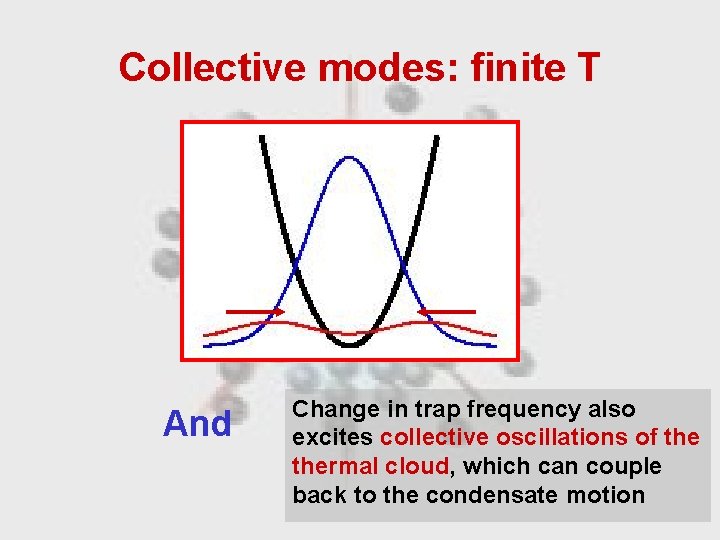
Collective modes: finite T And Change in trap frequency also excites collective oscillations of thermal cloud, which can couple back to the condensate motion

ZNG Formalism Bose broken symmetry: condensate wavefunction: condensate density: thermal cloud densities: ‘normal’ ‘anomalous’ Dynamical Equations E. Zaremba, T. Nikuni, and A. Griffin, JLTP 116, 277 (1999)

ZNG Formalism Generalized Gross-Pitaevskii equation: Popov approximation: E. Zaremba, T. Nikuni, and A. Griffin, JLTP 116, 277 (1999)

ZNG Formalism Boltzmann kinetic equation: Hartree-Fock excitations: moving in effective potential: phase space density: (semiclassical approx. ) E. Zaremba, T. Nikuni, and A. Griffin, JLTP 116, 277 (1999)

ZNG Formalism Boltzmann kinetic equation: E. Zaremba, T. Nikuni, and A. Griffin, JLTP 116, 277 (1999)

ZNG Formalism Coupling: mean field coupling E. Zaremba, T. Nikuni, and A. Griffin, JLTP 116, 277 (1999)

ZNG Formalism Coupling: Collisional coupling (atom transfer) E. Zaremba, T. Nikuni, and A. Griffin, JLTP 116, 277 (1999)

Numerical Methods Follow system dynamics in discrete time steps: 1. Solve GP equation for with FFT split-operator method 2. Evolve Kinetic equation using N-body simulations: • Collisionless dynamics – integrate Newton’s equations using a symplectic algorithm • Collisions – included using Monte Carlo sampling 3. Include mean field coupling between condensate and thermal cloud B. Jackson and E. Zaremba, PRA 66, 033606 (2002).

Applications Numerical simulations useful in understanding the following experiments, that studied collective modes at finite-T: • Scissors modes (Oxford): O. M. Maragò et al. , PRL 86, 3938 (2001). • Quadrupole modes (JILA): D. S. Jin et al. , PRL 78, 764 (1997). • Transverse breathing mode (ENS): F. Chevy et al. , PRL 88, 250402 (2002).

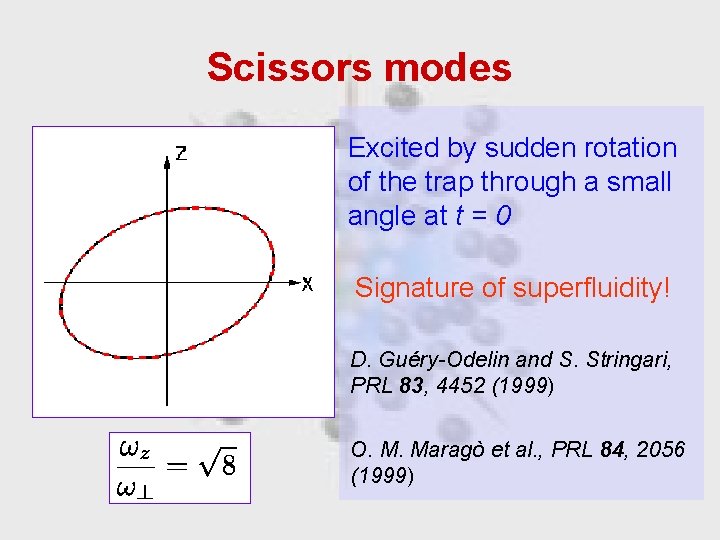
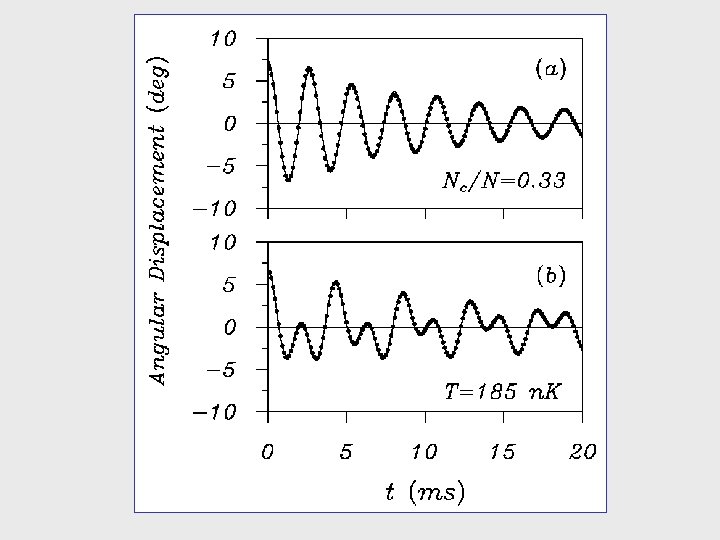
Scissors modes Excited by sudden rotation of the trap through a small angle at t = 0 Signature of superfluidity! D. Guéry-Odelin and S. Stringari, PRL 83, 4452 (1999) O. M. Maragò et al. , PRL 84, 2056 (1999)

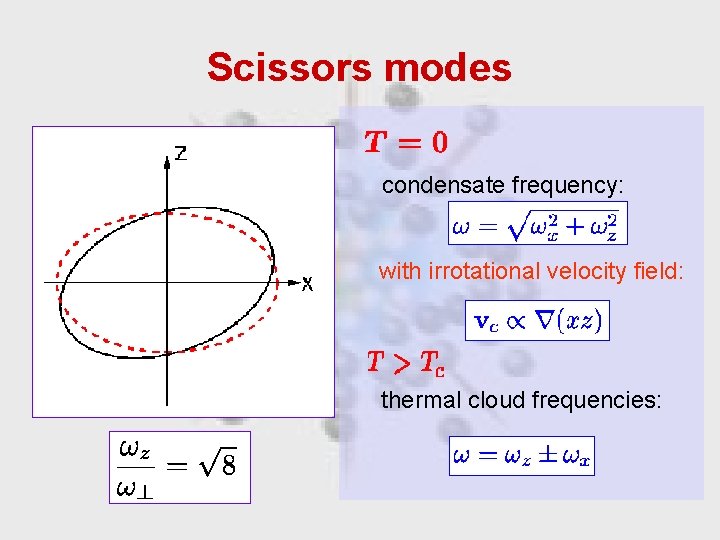
Scissors modes condensate frequency: with irrotational velocity field: thermal cloud frequencies:

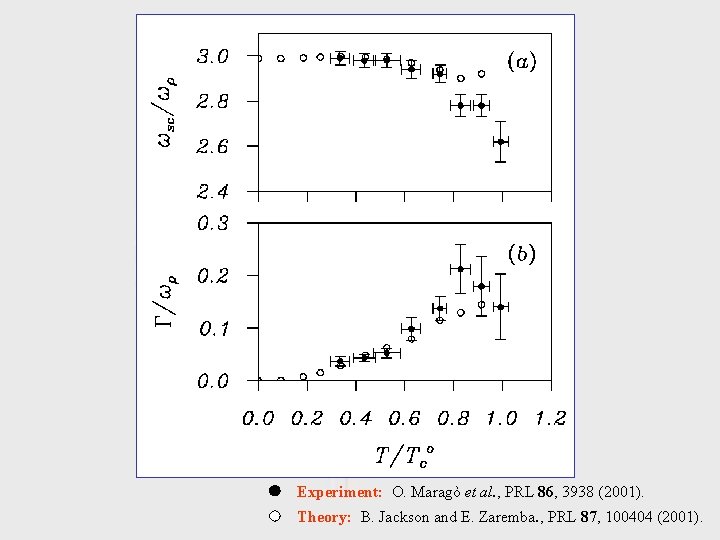
Experiment: O. Maragò et al. , PRL 86, 3938 (2001). Theory: B. Jackson and E. Zaremba. , PRL 87, 100404 (2001).

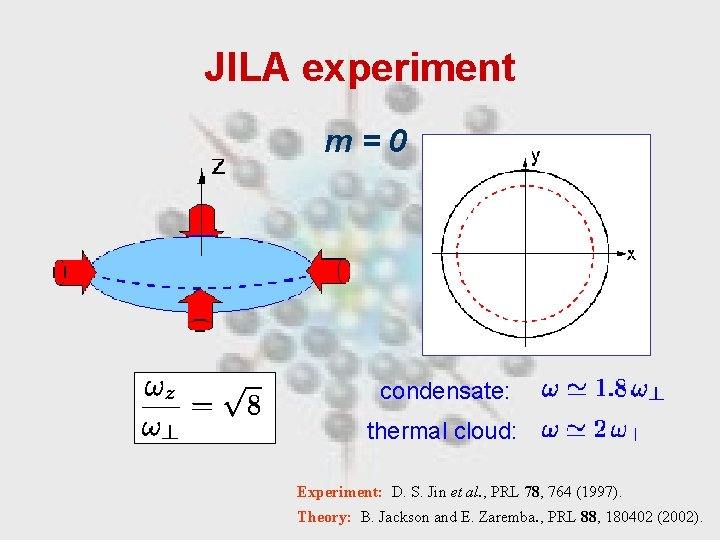
JILA experiment m=0 condensate: thermal cloud: Experiment: D. S. Jin et al. , PRL 78, 764 (1997). Theory: B. Jackson and E. Zaremba. , PRL 88, 180402 (2002).

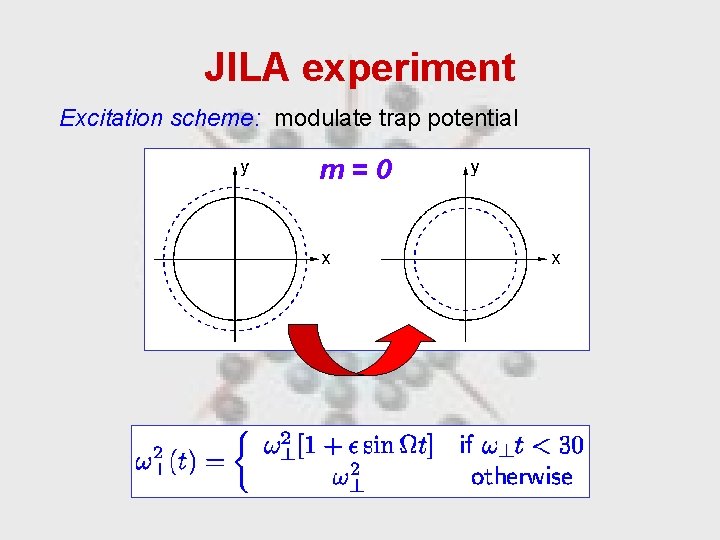
JILA experiment Excitation scheme: modulate trap potential m=0

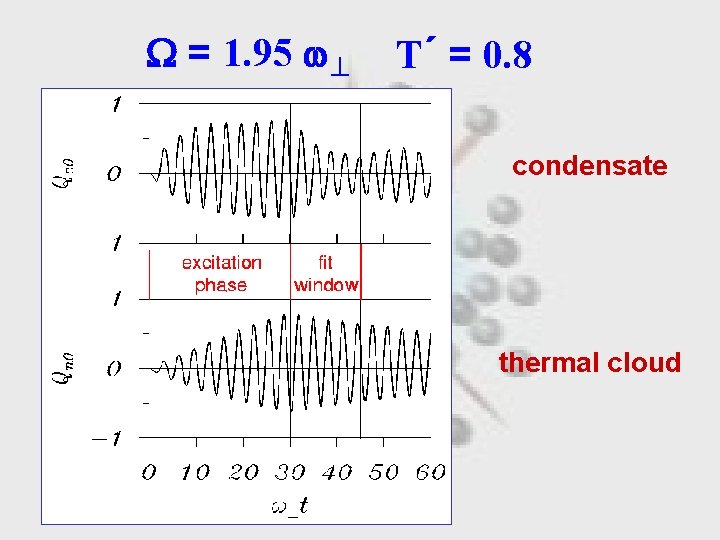
= 1. 95 T´ = 0. 8 condensate thermal cloud

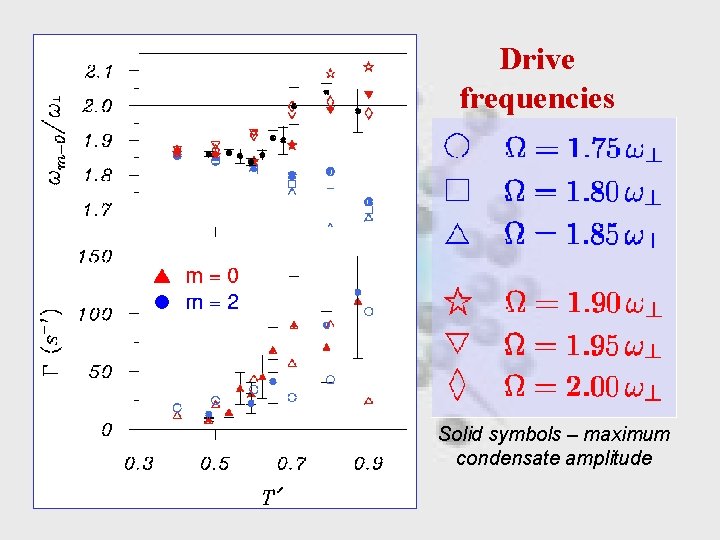
Drive frequencies Solid symbols – maximum condensate amplitude

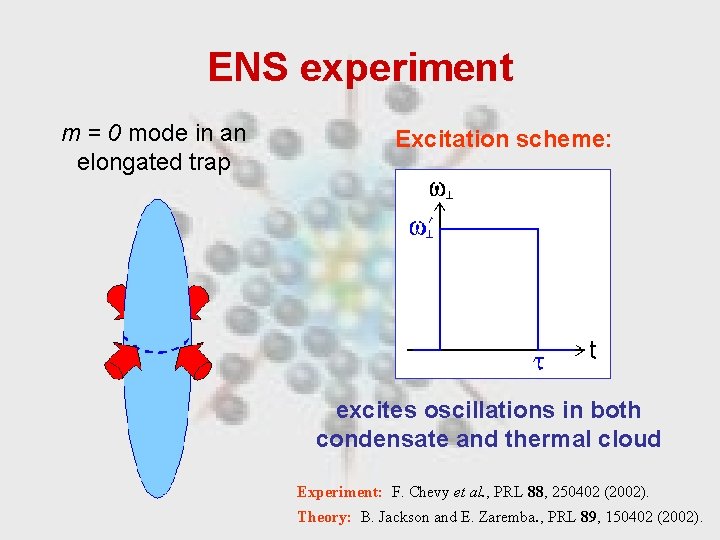
ENS experiment m = 0 mode in an elongated trap Excitation scheme: excites oscillations in both condensate and thermal cloud Experiment: F. Chevy et al. , PRL 88, 250402 (2002). Theory: B. Jackson and E. Zaremba. , PRL 89, 150402 (2002).

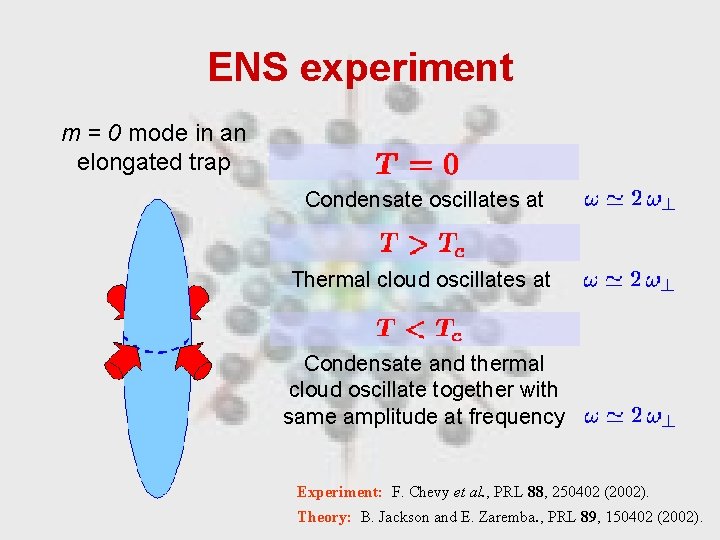
ENS experiment m = 0 mode in an elongated trap Condensate oscillates at Thermal cloud oscillates at Condensate and thermal cloud oscillate together with same amplitude at frequency Experiment: F. Chevy et al. , PRL 88, 250402 (2002). Theory: B. Jackson and E. Zaremba. , PRL 89, 150402 (2002).

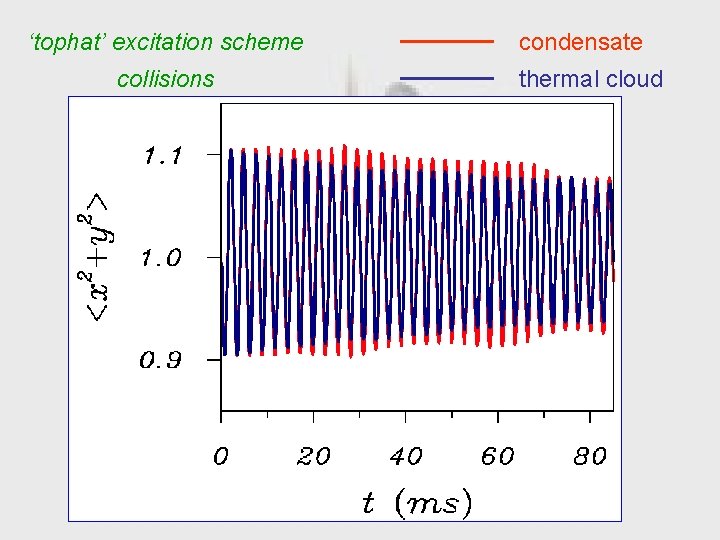
‘tophat’ excitation scheme collisions condensate thermal cloud

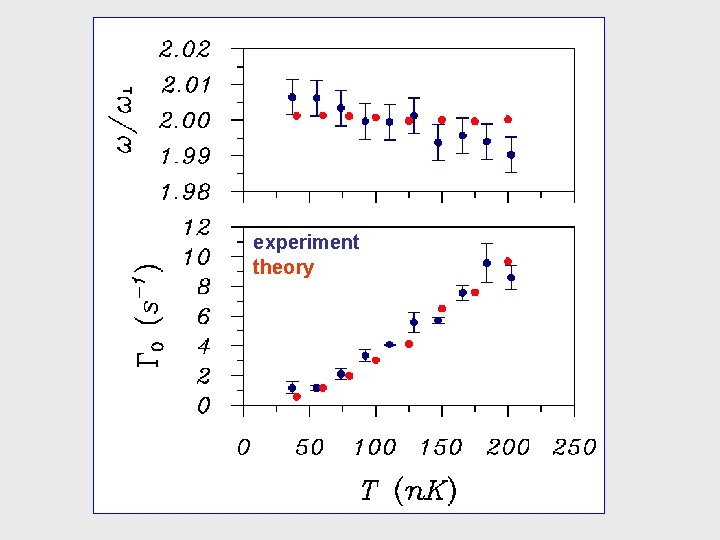
experiment theory

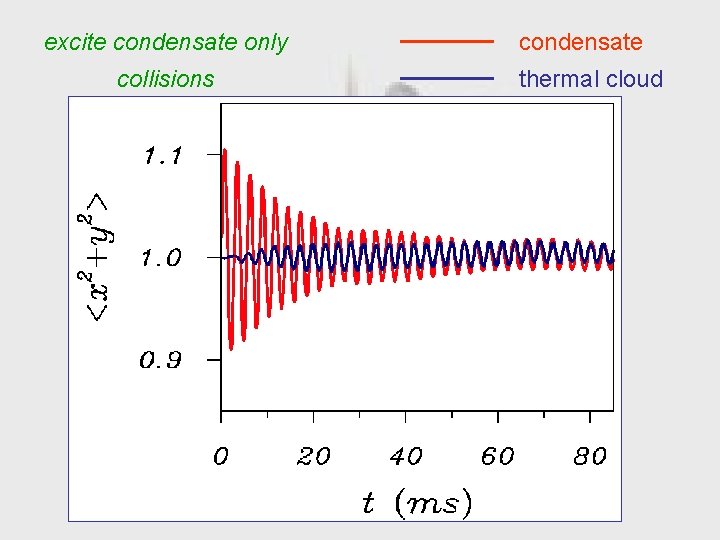
excite condensate only collisions condensate thermal cloud

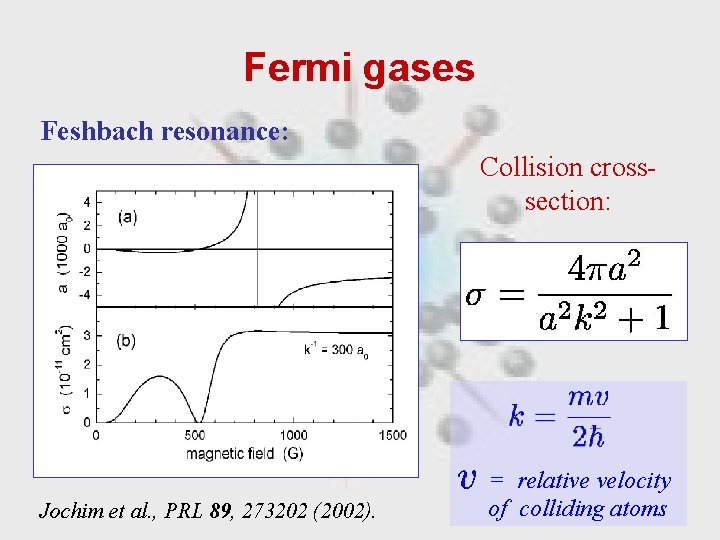
Fermi gases Motivation: Experiment by O’Hara et al. , Science 298, 2179 (2002). • Cool 6 Li atoms (50 -50 mixture of 2 hyperfine states) to quantum degeneracy T « TF • Static B-field tuned close to Feshbach resonance, a~ -104 a 0 • Observe anisotropic expansion of the cloud

Fermi gases Motivation: Experiment by O’Hara et al. , Science 298, 2179 (2002). • Cool 6 Li atoms (50 -50 mixture of 2 hyperfine states) to quantum degeneracy T « TF • Static B-field tuned close to Feshbach resonance, a~ -104 a 0 • Observe anisotropic expansion of the cloud Hydrodynamic behaviour, implying either: Ø Gas is superfluid (BCS or BEC) Ø Gas is normal, but collisions are frequent

Fermi gases Feshbach resonance: Collision crosssection: Jochim et al. , PRL 89, 273202 (2002). = relative velocity of colliding atoms

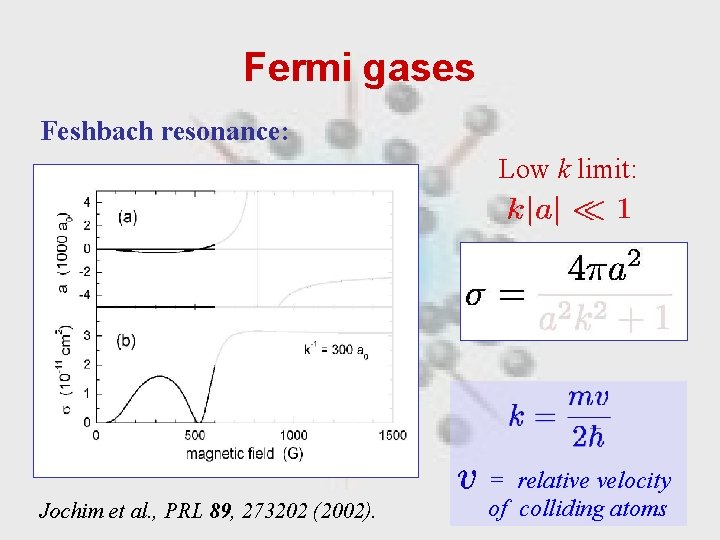
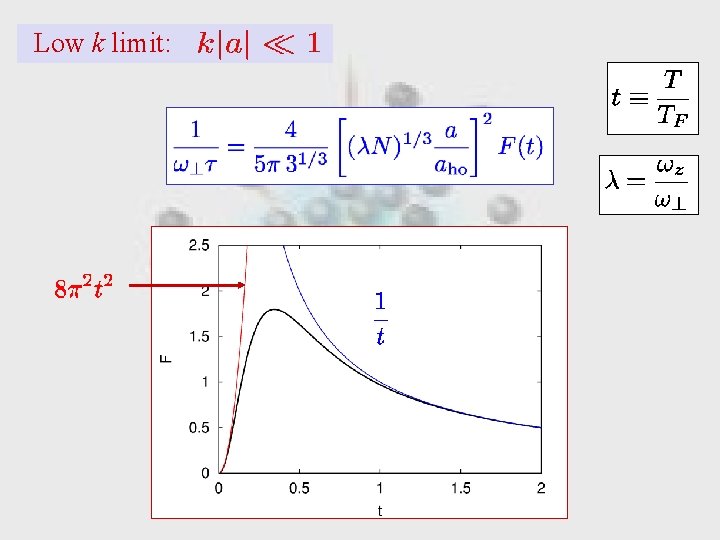
Fermi gases Feshbach resonance: Low k limit: Jochim et al. , PRL 89, 273202 (2002). = relative velocity of colliding atoms

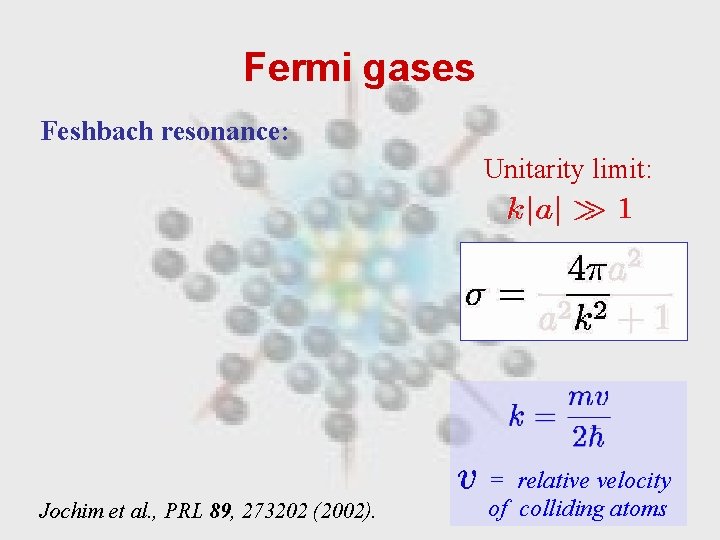
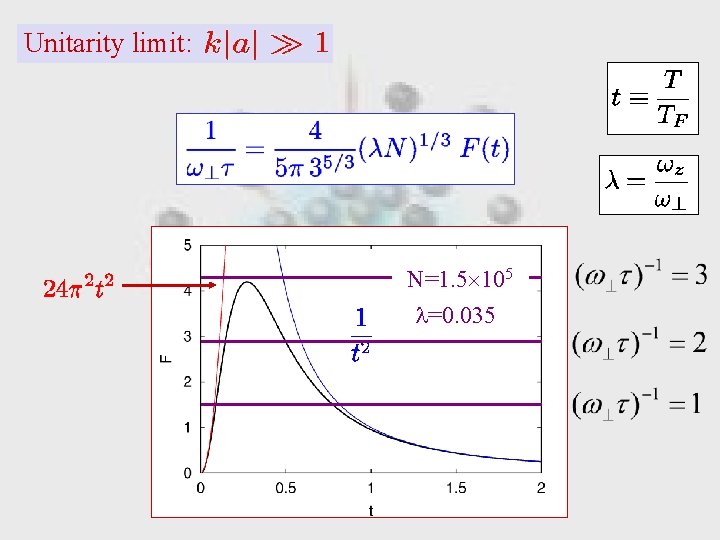
Fermi gases Feshbach resonance: Unitarity limit: Jochim et al. , PRL 89, 273202 (2002). = relative velocity of colliding atoms

Quadrupole collective modes: In-phase modes: L. Vichi, JLTP 121, 177 (2000)

Taking moments:

Taking moments:

Solve set of equations for Example: transverse breathing mode in a cigar-shaped trap • collisionless limit: ωτ » 1 • hydrodynamic limit: ωτ « 1 • intermediate regime: ωτ ~ 1

Low k limit:

Unitarity limit: N=1. 5 105 =0. 035

Summary • Bose condensates at finite temperatures: Ø studied damping and frequency shifts of various collective modes Ø Comparison with experiment shows good to excellent agreement, illustrating utility of scheme • Normal Fermi gases: Ø relaxation times of collective modes Ø simulations Ø rotation, optical lattices, superfluid component…