DYNAMICS OF MACHINES By Dr K SRINIVASAN Professor

DYNAMICS OF MACHINES By Dr. K. SRINIVASAN, Professor, AU-FRG Inst. for CAD/CAM, Anna University BALANCING OF RECIPROCATING MASSES

ØSINGLE CYLINDER ENGINE ØIN-LINE ENGINES 3 , 4 , 5, 6 cylinders are Common ØV-ENGINES – 4, 6, 8, 10, 12 , 16 with 6 & 8 being popular ØRADIAL ENGINES-

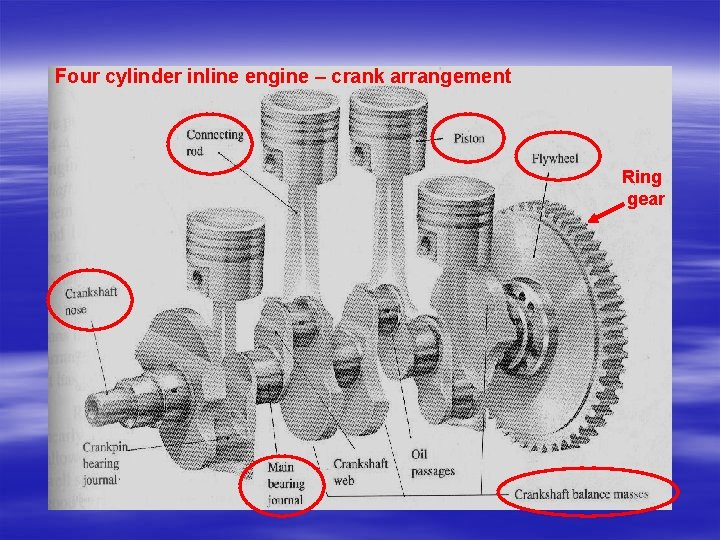
Four cylinder inline engine – crank arrangement Ring gear

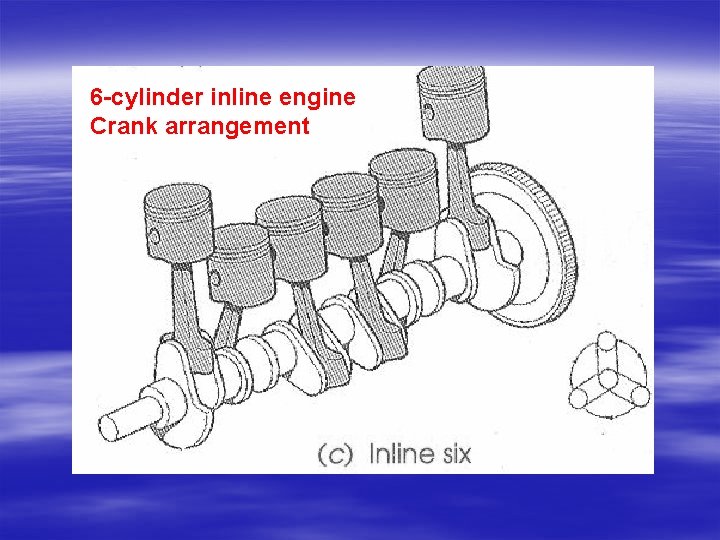
6 -cylinder inline engine Crank arrangement

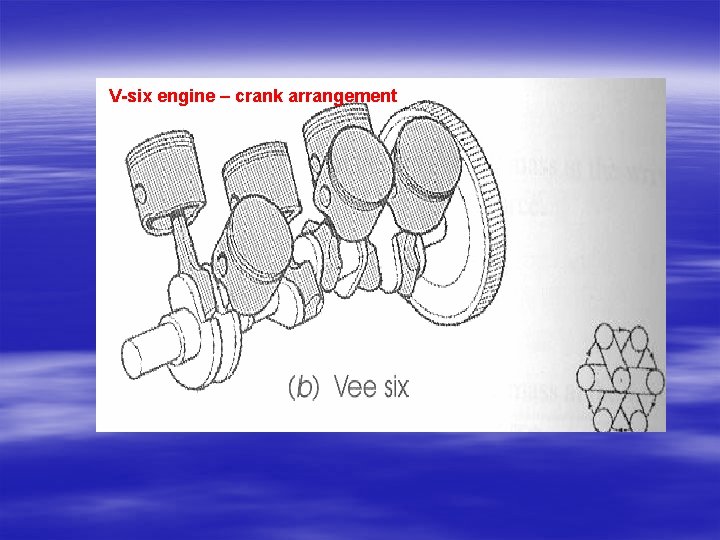
V-six engine – crank arrangement

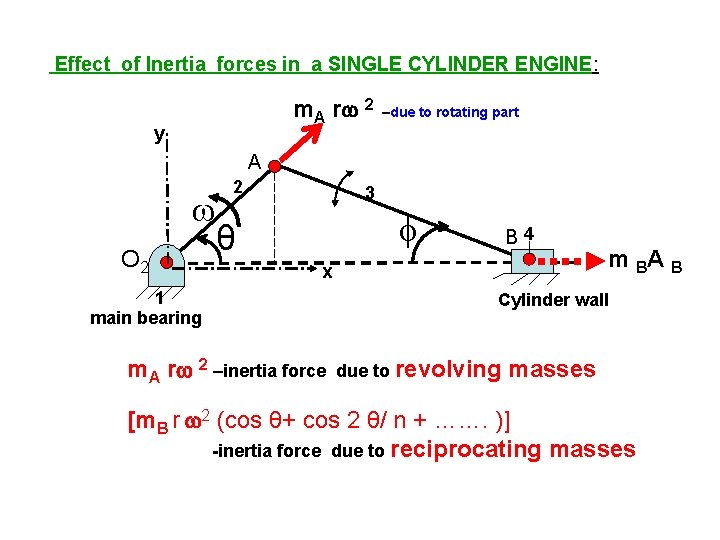
Effect of Inertia forces in a SINGLE CYLINDER ENGINE: m. A r 2 y –due to rotating part A 2 O 2 3 θ B 4 x 1 main bearing m. A r 2 –inertia force m BA B Cylinder wall due to revolving masses [m. B r 2 (cos θ+ cos 2 θ/ n + ……. )] -inertia force due to reciprocating masses

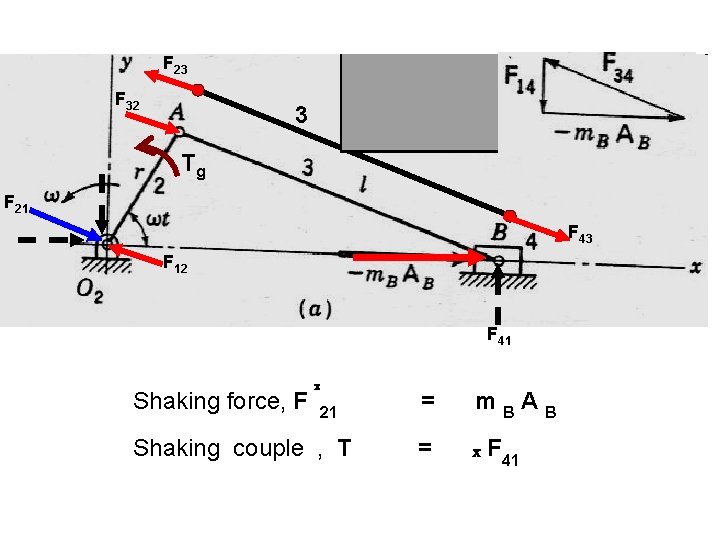
F 23 F 32 3 Tg F 21 F 43 F 12 F 41 Shaking force, F x 21 Shaking couple , T = m. BAB = x F 41

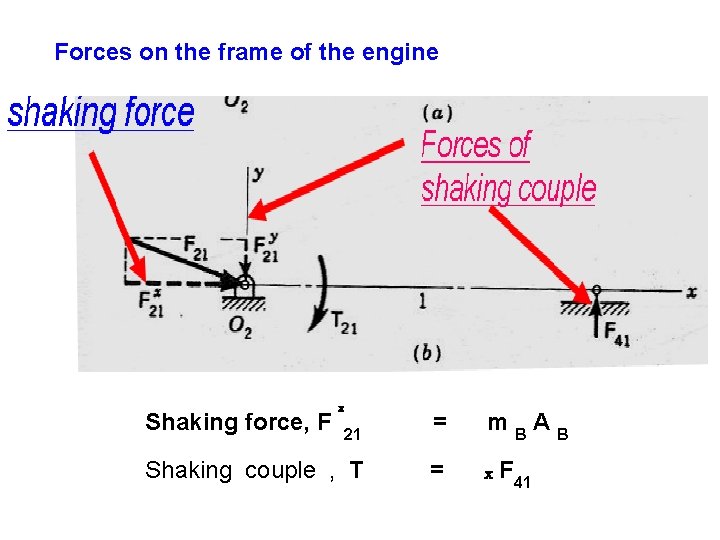
Forces on the frame of the engine Shaking force, F x 21 = m. BAB Shaking couple , T = x F 41

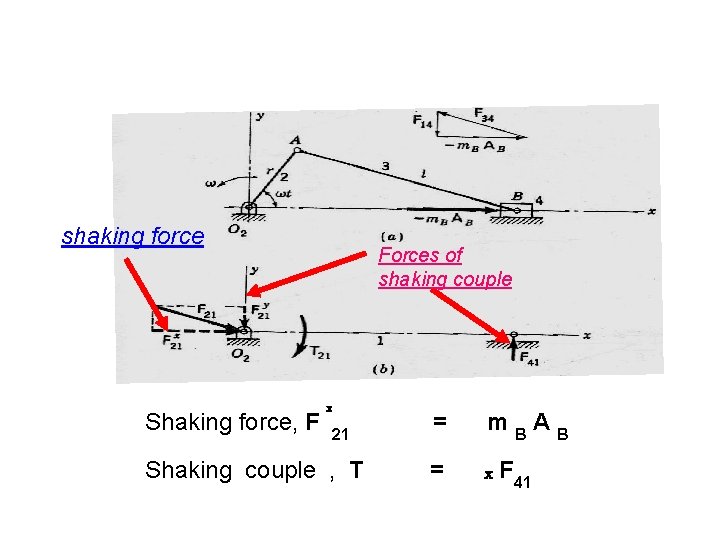
shaking force Shaking force, F Forces of shaking couple x 21 Shaking couple , T = m. BAB = x F 41

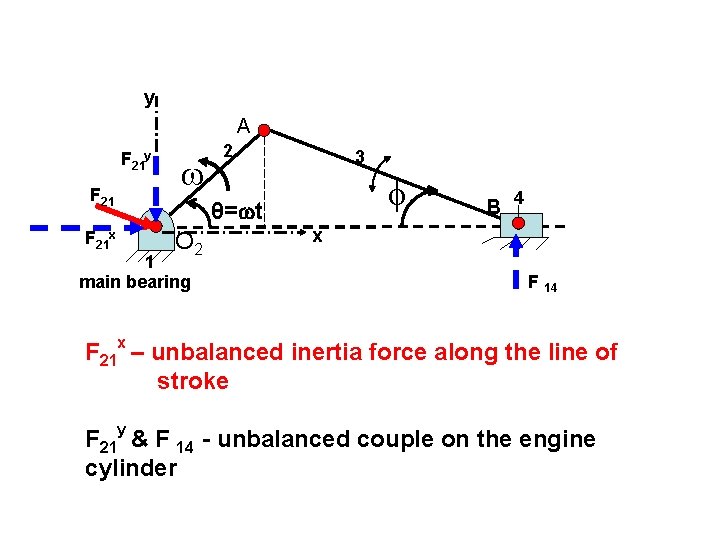
y A F 21 y F 21 x 2 3 θ= t O 2 1 main bearing B 4 x F 14 F 21 x – unbalanced inertia force along the line of stroke F 21 y & F 14 - unbalanced couple on the engine cylinder

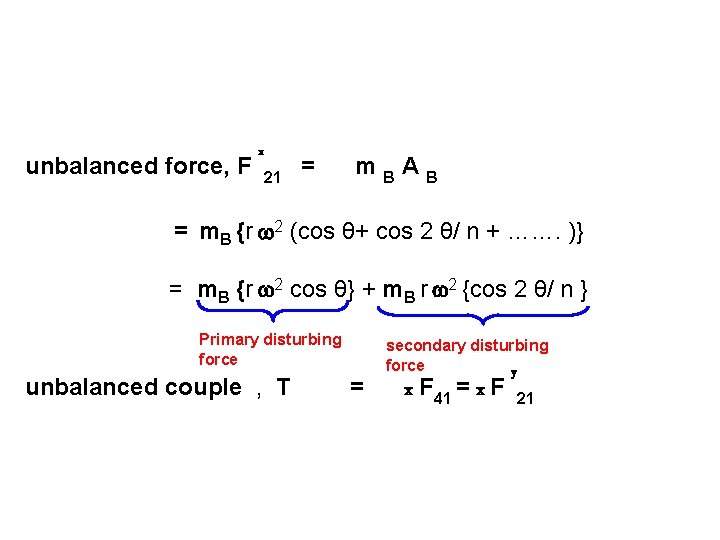
unbalanced force, F x 21 = m. BAB = m. B {r 2 (cos θ+ cos 2 θ/ n + ……. )} = m. B {r 2 cos θ} + m. B r 2 {cos 2 θ/ n } Primary disturbing force unbalanced couple , T = secondary disturbing force y x F 41 = x F 21

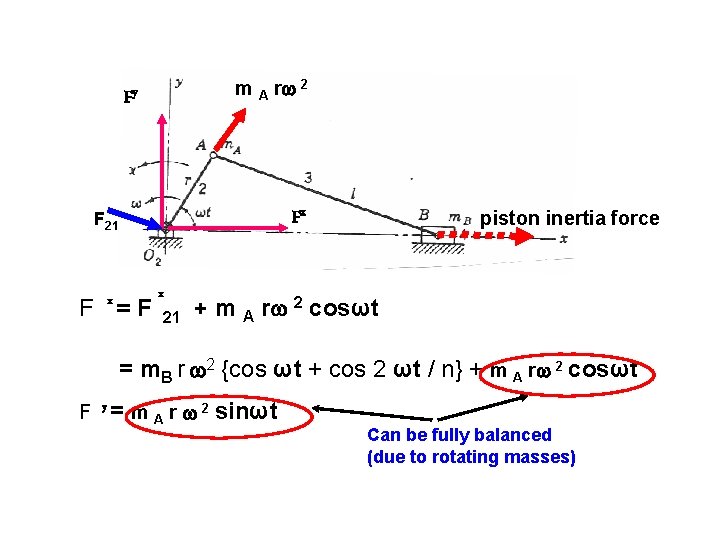
m A r 2 Fy Fx F 21 x F =F x 21 piston inertia force + m A r 2 cosωt = m. B r 2 {cos ωt + cos 2 ωt / n} + m A r 2 cosωt F y = m A r 2 sinωt Can be fully balanced (due to rotating masses)

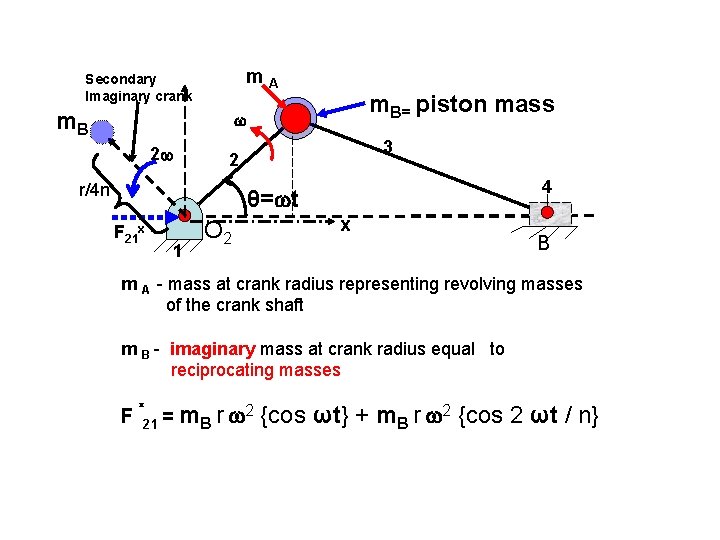
m. A Secondary Imaginary crank m. B= piston mass 2 3 2 r/4 n 4 θ= t F 21 x 1 O 2 x B m A - mass at crank radius representing revolving masses of the crank shaft m B - imaginary mass at crank radius equal to reciprocating masses F x 2 = m r 21 B {cos ωt} + m. B r 2 {cos 2 ωt / n}

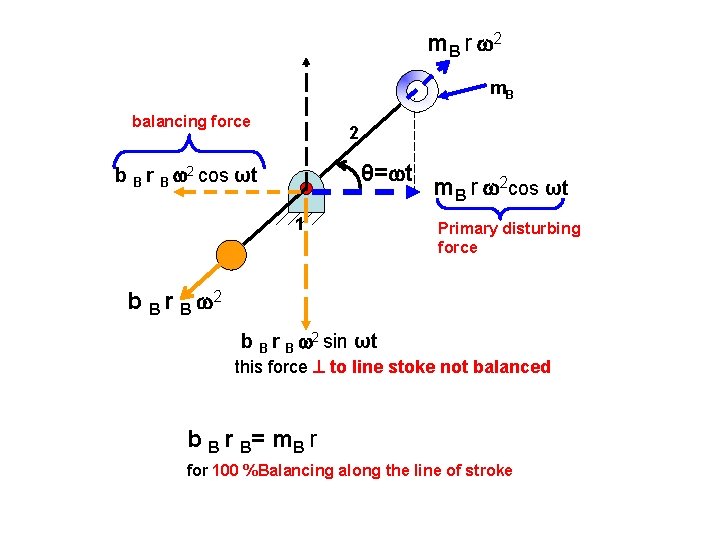
m B r 2 m. B balancing force 2 θ= t b B r B 2 cos ωt 1 m. B r 2 cos ωt Primary disturbing force b B r B 2 sin ωt this force to line stoke not balanced b B r B= m B r for 100 %Balancing along the line of stroke

Example : Data given : Engine : Single cylinder oil engine Stroke : 375 mm speed : 300 rpm Mass of the reciprocating parts : 68 kg Revolving parts : 81. 5 kg at crank radius Radius at which balance mass to be introduced at 180 o : 150 mm Nature of balancing to be obtained : whole of the revolving parts & one-half of the reciprocating parts To find : 1. required balancing mass 2. Residual unbalanced force on the main bearing

Solution : The total equivalent revolving mass at crank radius which has to be balanced = 81. 5 + 68 X 0. 5 = 115. 5 kg @ (375/2) mm radius We have. M b X r b = 115. 5 X (375 /2) Where M b is the balancing mass & r b is radius of the balancing mass Balancing mass @ 150 mm radius = 115. 5 X (375 /2) / 150 = 144. 375 kg Contd. .

Calculation of residual unbalanced force : = (2 X X 300 ) /60 =31. 4 rad /s Unbalanced force parallel to the line of stroke ( due to reciprocating mass) F parallel = [ ½ X {68 2 r cos }] Unbalanced force perpendicular to the line of stroke ( due to reciprocating mass) F perpendicular = [ ½ X {68 2 r sin }] Total unbalanced force , F = ½ X 68 2 r = ½ X 68 X 31. 4 2 X 0. 1875 = 6, 286 N

Balancing web

Engine specifications: one - cylinder four - stroke Bore : 75 mm Stroke : 88. 5 mm l / r : 3. 5 rpm : 3400 m A : 5 kg m B : 2. 1 kg

=43. 2 k N Variation of unbalanced force with crank rotation

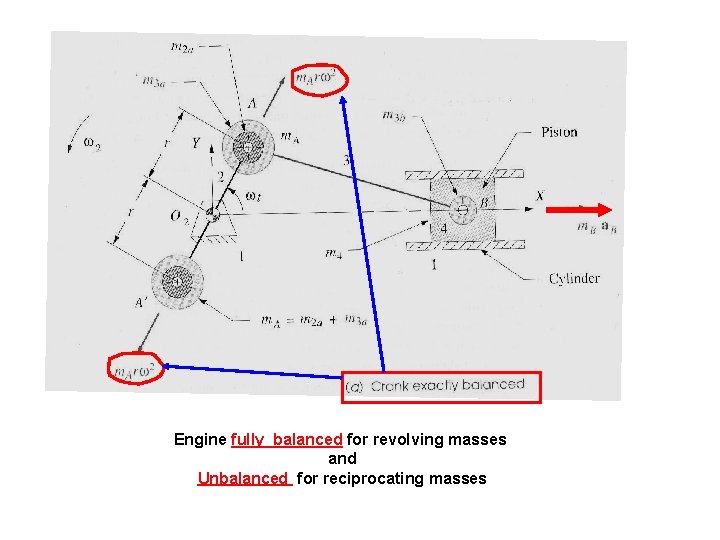
Engine fully balanced for revolving masses and Unbalanced for reciprocating masses

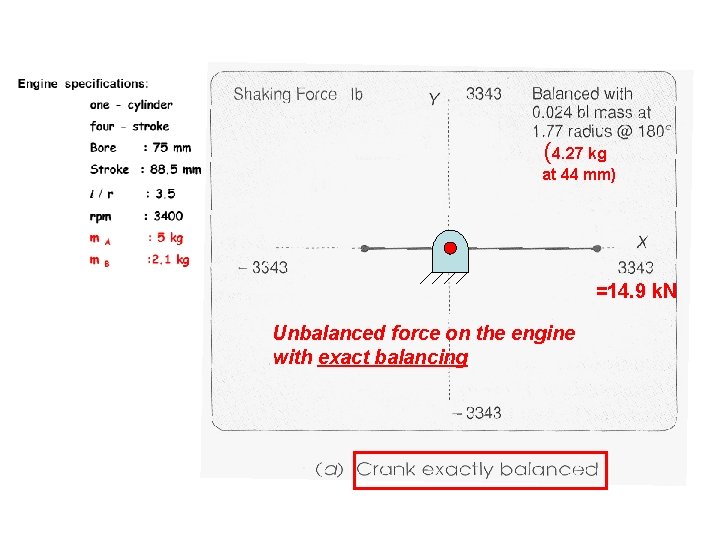
(4. 27 kg at 44 mm) =14. 9 k. N Unbalanced force on the engine with exact balancing

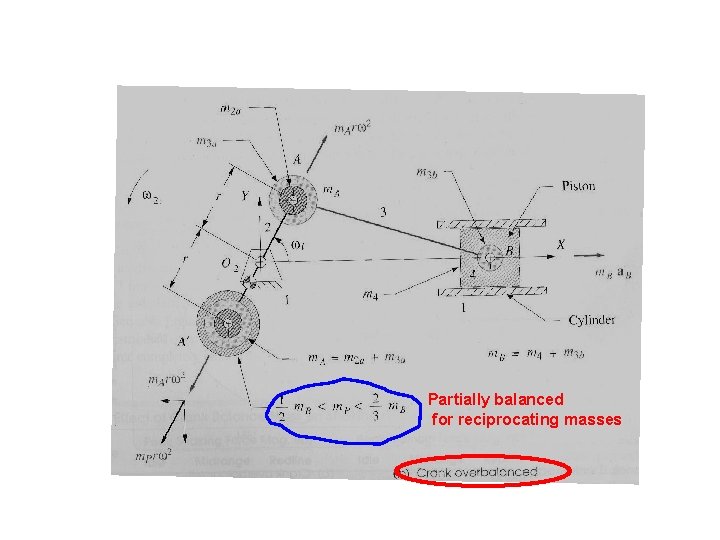
Partially balanced for reciprocating masses

(6. 4 kg at 44 mm) =7. 5 k. N unbalanced force on the engine with over balancing

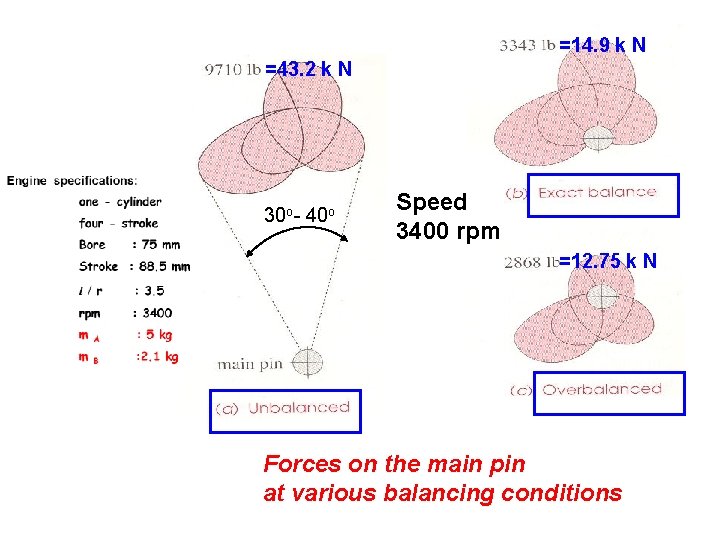
=14. 9 k N =43. 2 k N 30 o- 40 o Speed 3400 rpm =12. 75 k N Forces on the main pin at various balancing conditions

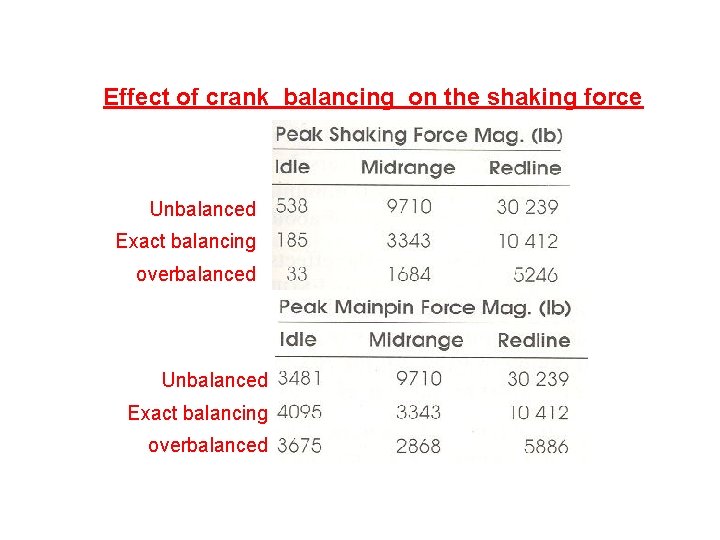
Effect of crank balancing on the shaking force Unbalanced Exact balancing overbalanced

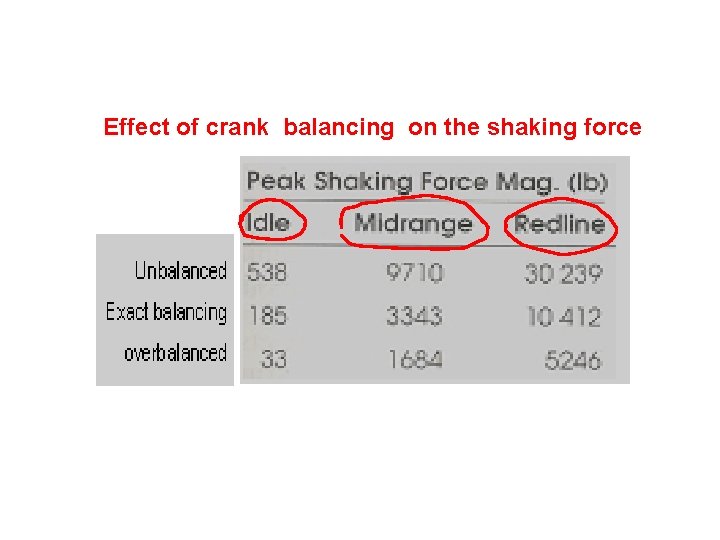
Effect of crank balancing on the shaking force

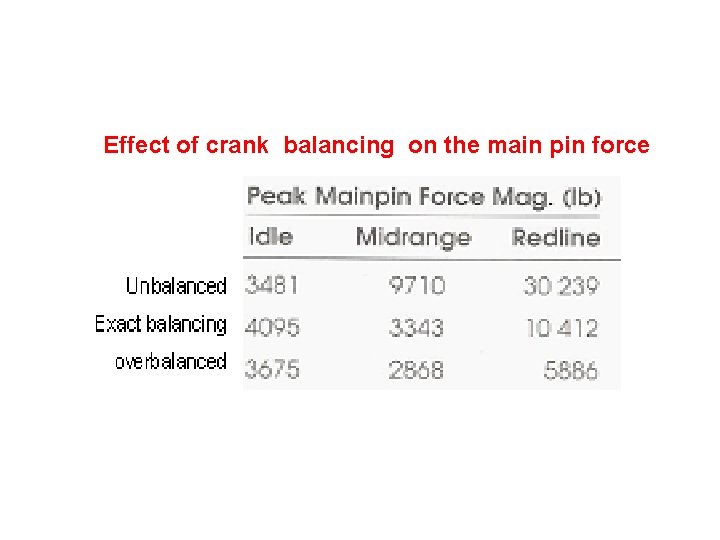
Effect of crank balancing on the main pin force

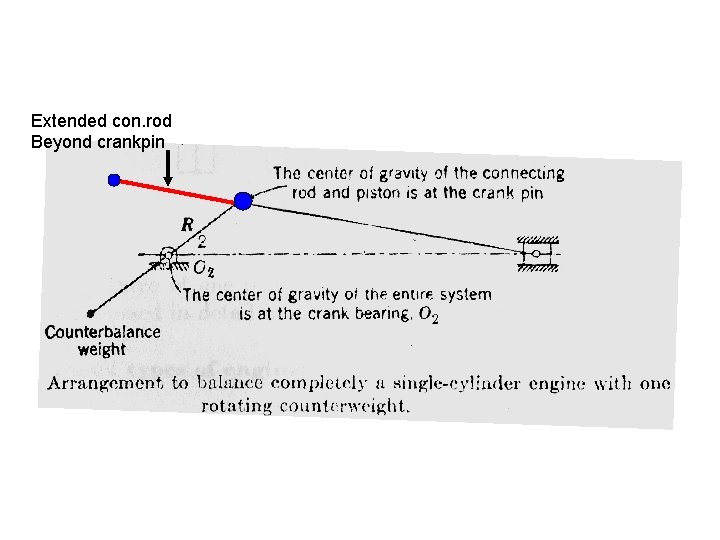
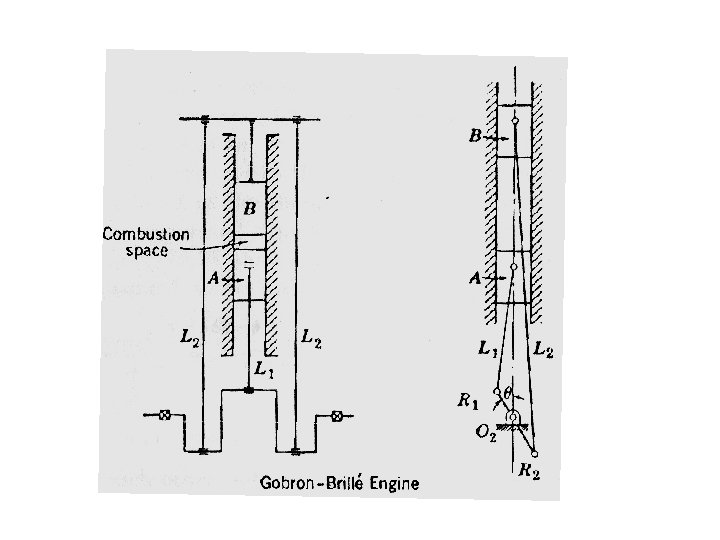
Extended con. rod Beyond crankpin

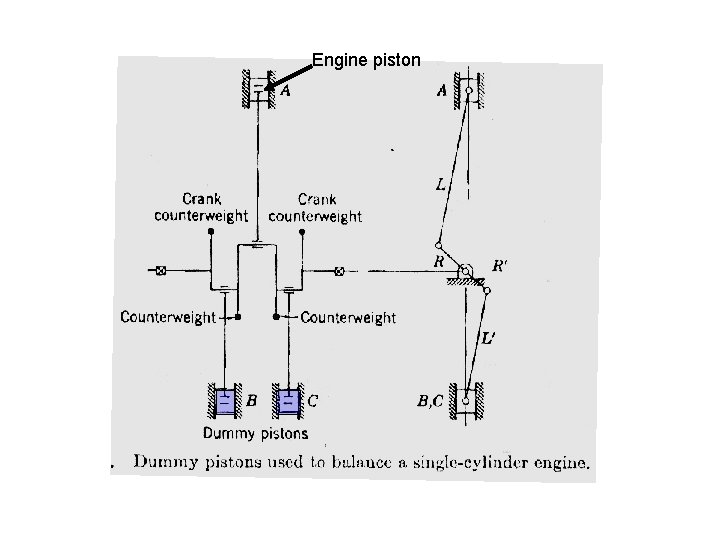
Engine piston

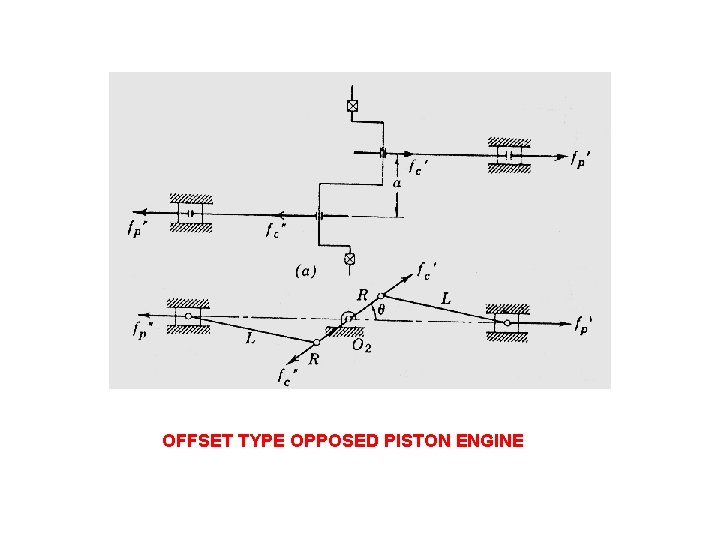
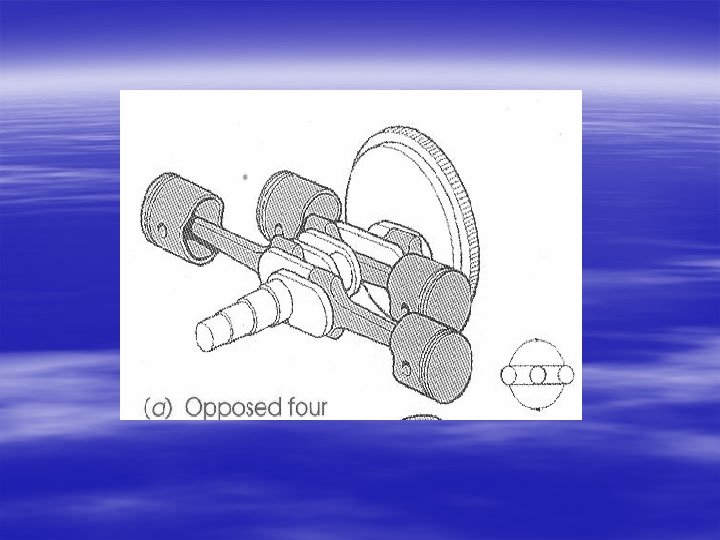
OFFSET TYPE OPPOSED PISTON ENGINE

MULTI CYLINDER IN-LINE ENGINES: Common crank shaft driven by number of connecting rods Angular interval between successive cranks , Ø(2 / n) in the case of 2 -stroke engine Ø(4 / n) in the case of 4 -stroke engine Where ‘n’ is the number of cylinders firing order influences balancing condition

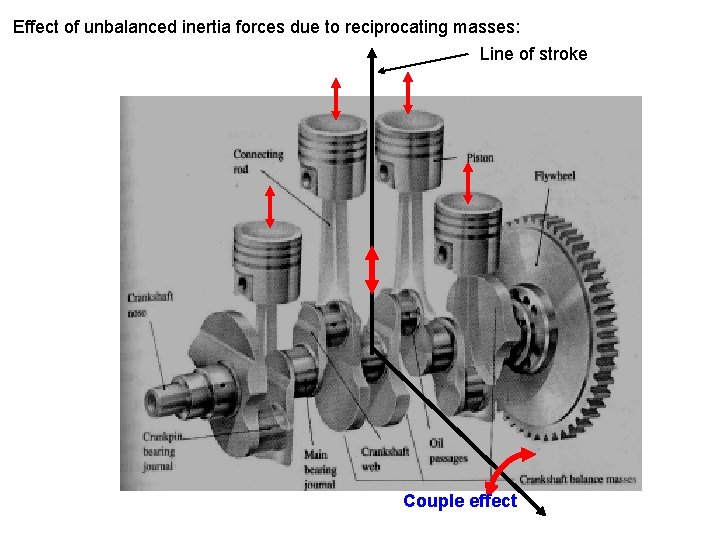
Effect of unbalanced inertia forces due to reciprocating masses: Line of stroke Couple effect

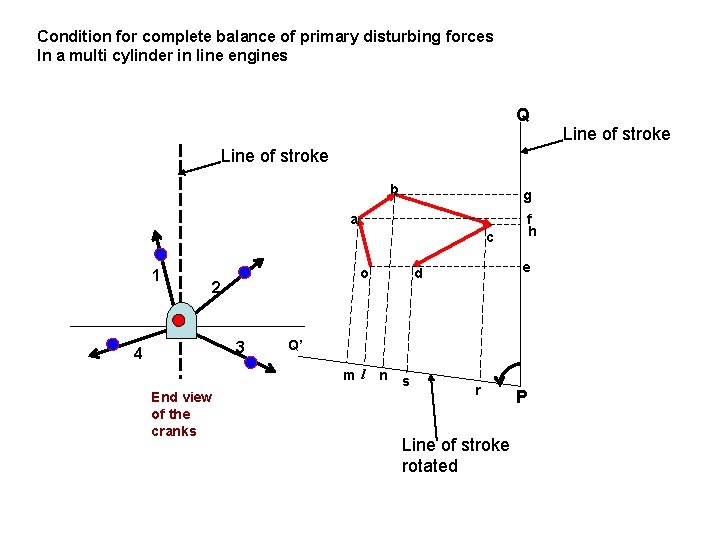
Condition for complete balance of primary disturbing forces In a multi cylinder in line engines Q Line of stroke b g a c 1 o 2 3 4 e d Q’ ml End view of the cranks f h n s r Line of stroke rotated P Line of stroke