Dynamics of Double Inverted Pendulum Kevin Luna Mentor

Dynamics of Double Inverted Pendulum Kevin Luna (Mentor) Zach Kirch Devin Johnson

Background of Inverted Pendulum System - For Midterm paper, analyzed a simple Inverted Pendulum system, and the dynamics of such a system. - Briefly will walk through the methodology and results found, as we plan to incorporate a similar process for the Double Inverted Pendulum System.

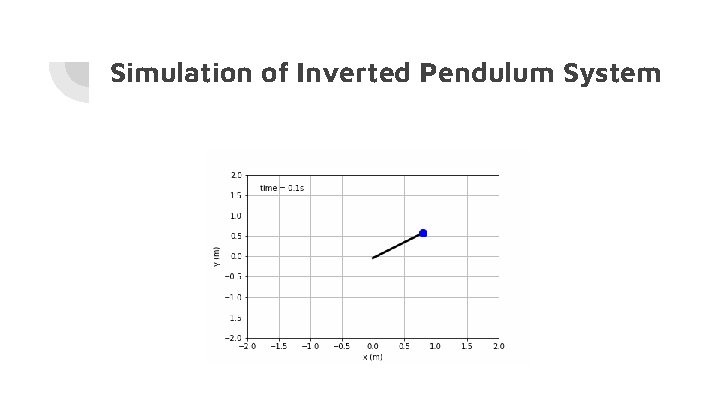
Simulation of Inverted Pendulum System

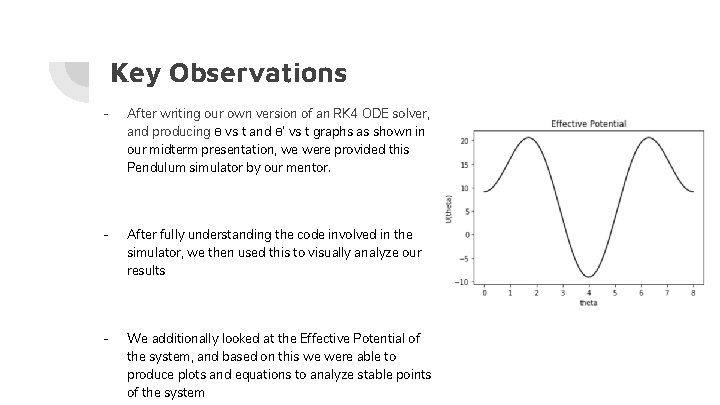
Key Observations - After writing our own version of an RK 4 ODE solver, and producing θ vs t and θ’ vs t graphs as shown in our midterm presentation, we were provided this Pendulum simulator by our mentor. - After fully understanding the code involved in the simulator, we then used this to visually analyze our results - We additionally looked at the Effective Potential of the system, and based on this we were able to produce plots and equations to analyze stable points of the system

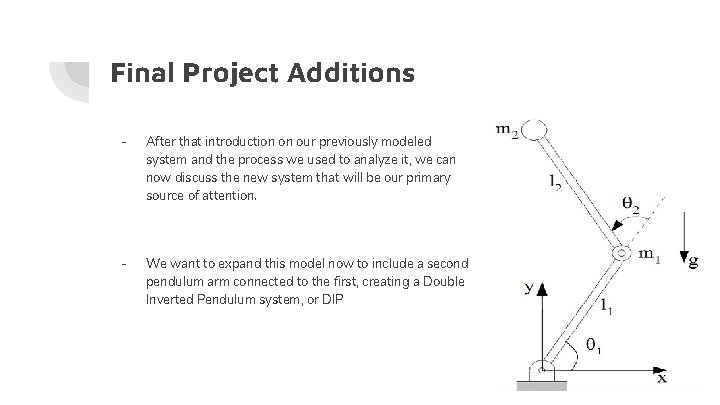
Final Project Additions - After that introduction on our previously modeled system and the process we used to analyze it, we can now discuss the new system that will be our primary source of attention. - We want to expand this model now to include a second pendulum arm connected to the first, creating a Double Inverted Pendulum system, or DIP

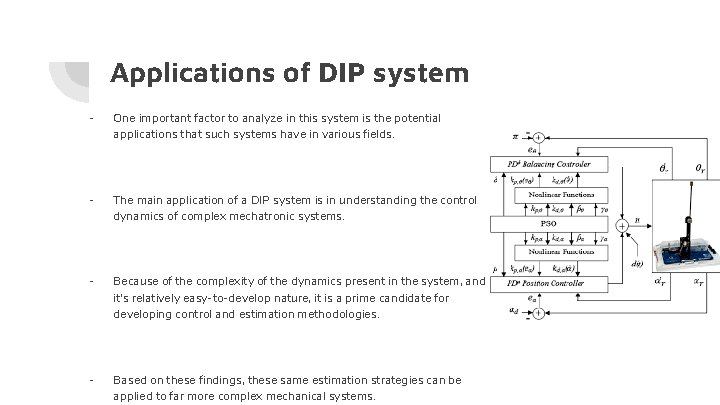
Applications of DIP system - One important factor to analyze in this system is the potential applications that such systems have in various fields. - The main application of a DIP system is in understanding the control dynamics of complex mechatronic systems. - Because of the complexity of the dynamics present in the system, and it’s relatively easy-to-develop nature, it is a prime candidate for developing control and estimation methodologies. - Based on these findings, these same estimation strategies can be applied to far more complex mechanical systems.

Current Research - Most of the current research on this topic is centered around creating a controller base that will keep the DIP system in a equilibrium state - These types of controllers, such as the Linear Quadratic Regulator (LQR) controller, have far reaching benefits in defense and aeronautical applications.

DIP Equations of Motion

DIP Dynamics As the first arm moves it exerts a force on the second arm, effectively acting as that arm’s base so there exists a combination of frequency and amplitude where the second arm moves freely to the fixed first arm. . Energy in the system can be analyzed as whole system or part by part. The angle of the arm could be measured from y axis or from perpendicular to first arm but the latter creates much more tedious math.

DIP Lagrangians <Insert Lots of tedious math> Lagrangian for system with no vibration induced at the base: <Insert even more tedious math> Lagrangian for system with vibrations (a cos Ωt) induced at the base:

Equations to input into ODE solver - Now that we have obtained the Lagrangian of the vibrating base DIP system, we obtain the following equations that can be used as inputs into the ODE solving software: - The system is then written as four coupled 1 st Order ODEs, as seen in the segment of script on the next slide.

Python Script - Essentially, the same Python script was used to produce plots for how the system would behave for various sets of parameters. Major difference was the fact that there were two simultaneous equations being solved at the same time.

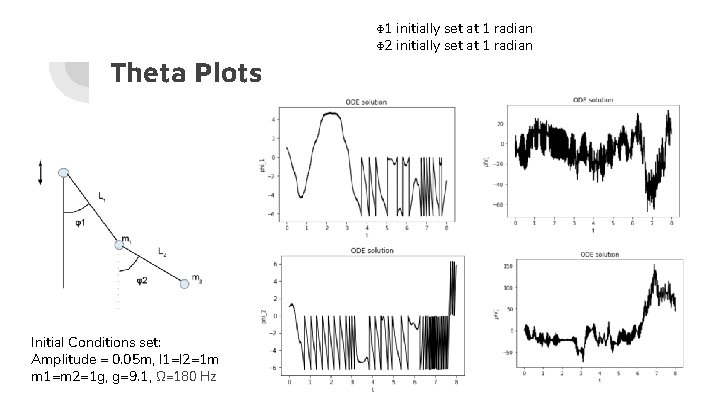
Theta Plots Initial Conditions set: Amplitude = 0. 05 m, l 1=l 2=1 m m 1=m 2=1 g, g=9. 1, Ω=180 Hz Φ 1 initially set at 1 radian Φ 2 initially set at 1 radian

Cartesian Plot of End of Arm

Final Steps - Overall goal of the project was to analyze the stability of the DIP system, but that might not be realistic at this point. Would have to derive Effective Potential for DIP system, which is exceedingly more complex to analyze in this regard. Possibly could do so by making certain assumptions about system to decrease complexity of the equations, but not entirely certain. Additionally, could analyze how changing amplitude/oscillation of base and masses/length of the pendulum arms would affect the resulting plots.

References B. Xu, Y. Lyu, S. Gadsden, “Estimation and Control of a Double-Inverted Pendulum”, CSME International Congress, 1 -6 (2018) K. Srikanth, G. Kumar, “Stabilization at Upright Equilibrium Position of a Double Inverted Pendulum with Unconstrained BAT optimization”, International Journal on Computational Science and Applications, 1 -15 (2015) Q. Li, W. Tao, C. Zhang, “Stabilization Control of Double Inverted Pendulum System”, IEEE, 18 (2008)