Dynamics Motion with Regard to Mass Particle Dynamics

Dynamics

Motion with Regard to Mass Particle Dynamics Mass concentrated in point Newton’s Equation Governs Motion f=Mx

Rigid Body Dynamics Two equations govern motion: Newton’s Equation for Translations F= M x Euler’s Equation for Rotational Motion T=Iw+w´Iw where I is the interial tensor that describes the distribution of mass

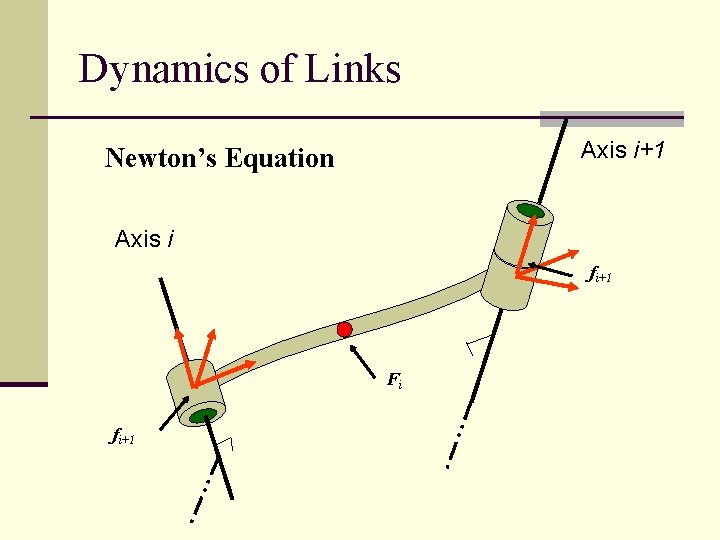
Dynamics of Links Axis i+1 Newton’s Equation Axis i fi+1 Fi fi+1

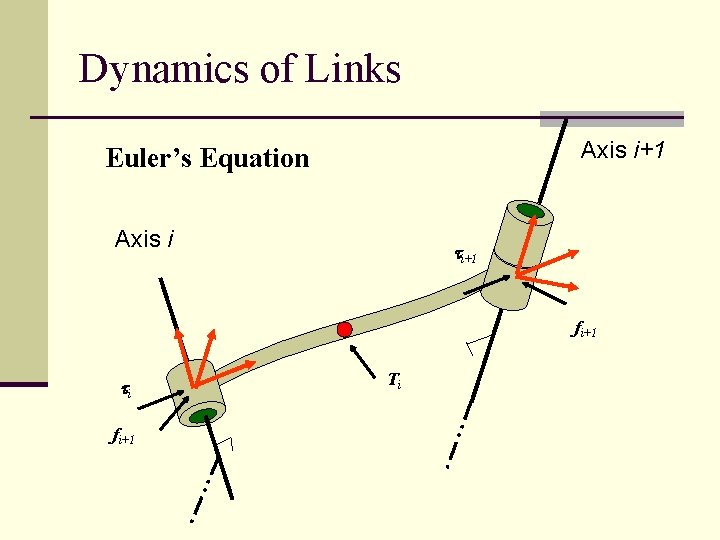
Dynamics of Links Axis i+1 Euler’s Equation Axis i ti+1 fi+1 ti fi+1 Ti

Bodies in space Conservation of Momentum 0=Mx A body in motion remains in motion Conservation of Angular Momentum 0=Iw The relationship between angular momentum and orientation is tricky

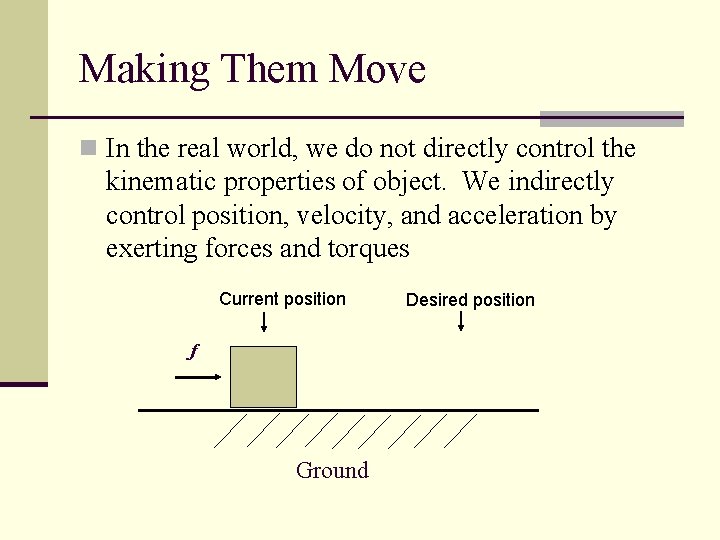
Making Them Move n In the real world, we do not directly control the kinematic properties of object. We indirectly control position, velocity, and acceleration by exerting forces and torques Current position f Ground Desired position

Controllers n What force should we apply to move the box to the destination? Current position f Ground Desired position

Proportional Control n A control law, function, or algorithm for computing forces (or torques). n Force is proportional to distance to goal: F = Kp ( xd – x) Workhorse of robotics and animation

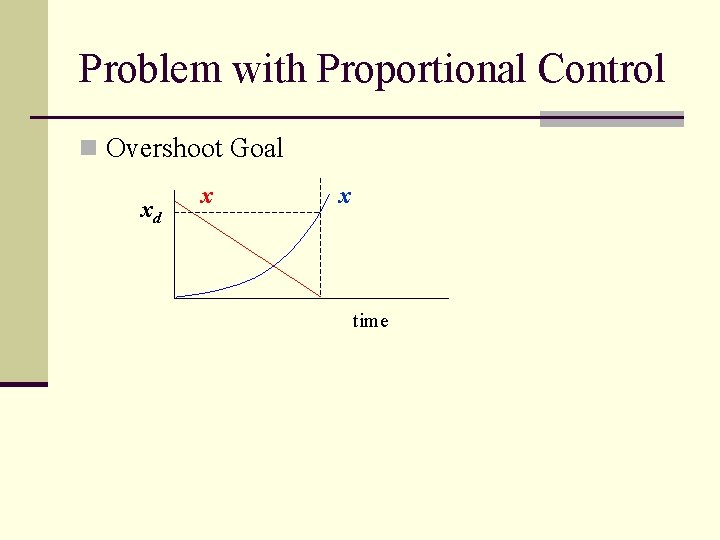
Problem with Proportional Control n Overshoot Goal xd x x time

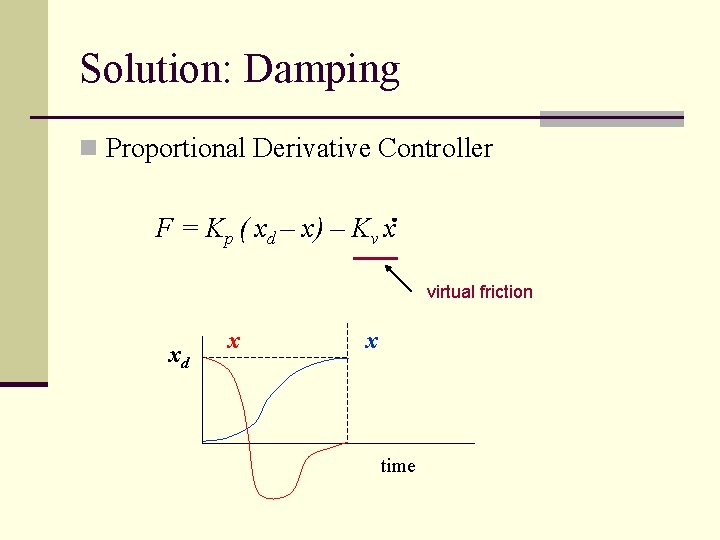
Solution: Damping n Proportional Derivative Controller F = Kp ( xd – x) – Kv x virtual friction xd x x time

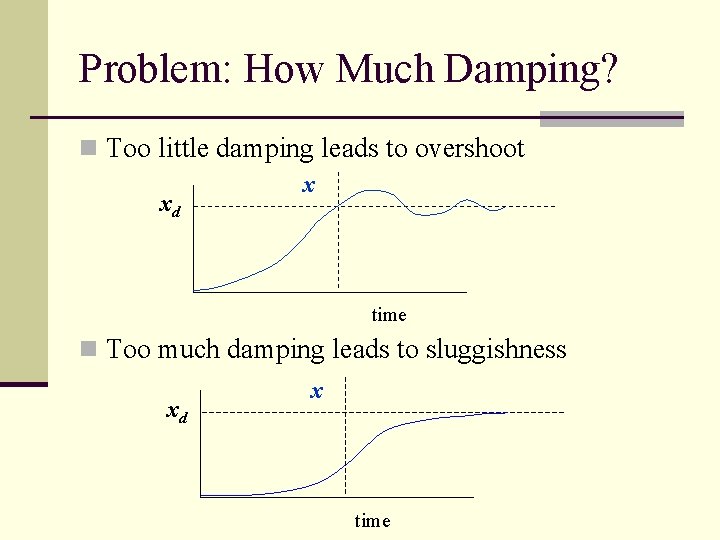
Problem: How Much Damping? n Too little damping leads to overshoot xd x time n Too much damping leads to sluggishness xd x time

Critical Damping n Constrain the constants such that: Kv 2 - 4 Kp = 0 Just right: No overshoot Fastest possible approach (given gain Kp)

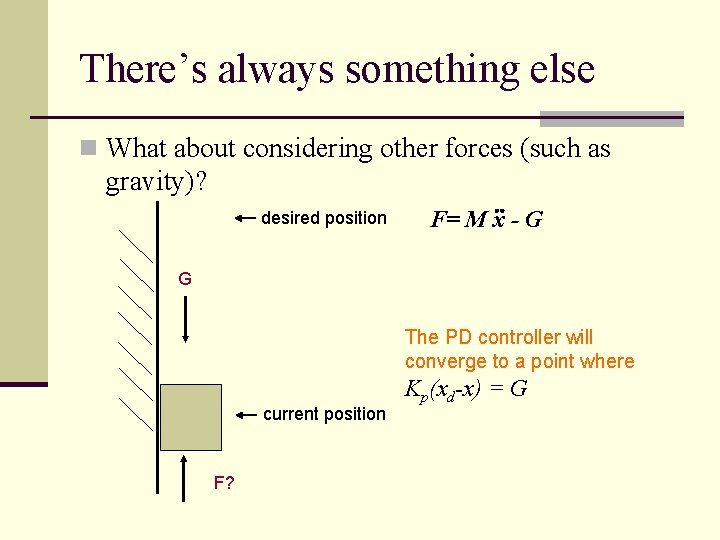
There’s always something else n What about considering other forces (such as gravity)? desired position F= M x - G G The PD controller will converge to a point where current position F? Kp(xd-x) = G

PID Control n Proportional Integral Derivative Control F = Kp ( xd – x) – Kv x + Ki ò ( xd – x) dt