Dynamics Intro Application of Newtons Laws Drawing FreeBodyDiagrams

Dynamics: Intro & Application of Newton’s Laws


Drawing Free-Body-Diagrams AP Physics Development Committee May 2010 – New Wording for free-body or force diagrams. (p. 149 C&E) Students will be directed to "draw and label the forces (not components) that act on the [object], " where [object] is replaced by a reference specific to the question, such as "the car when it reaches the top of the hill. " Any components that are included in the diagram will be scored in the same way as incorrect or extraneous forces.

Drawing Free-Body-Diagrams In addition, in any subsequent part asking for a solution that would typically make use of the diagram, the following will be included. "If you need to draw anything other than what you have shown in part [x] to assist in your solution, use the space below. Do NOT add anything to the figure in part [x]. " This will give students the opportunity to construct a working diagram showing any components that are appropriate to the solution of the problem. This second diagram will not be graded.

Drawing Free-Body-Diagrams Binder pp. 19 -21

Force = Interaction Force: interaction between an agent and an object causing a push or pull Two kinds of forces 1. Contact 2. “Non-Contact” (long-range field forces due to gravitational, magnetic, and/or electric fields)
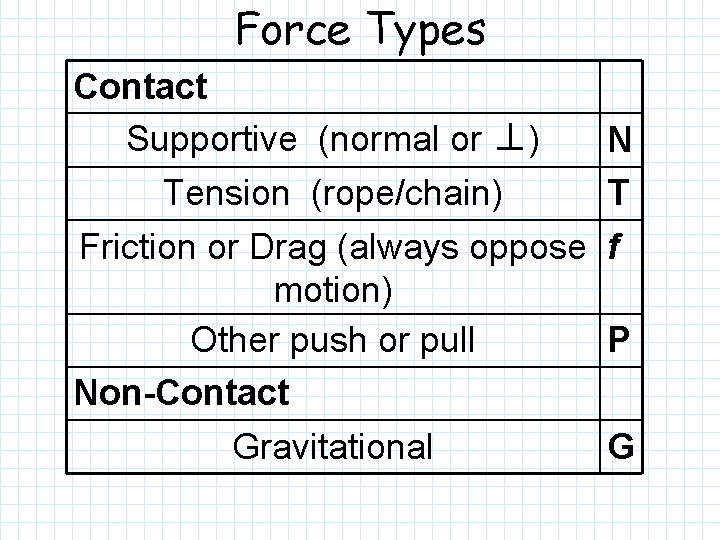
Force Types Contact Supportive (normal or ⊥) N Tension (rope/chain) T Friction or Drag (always oppose f motion) Other push or pull P Non-Contact Gravitational G

System Schema block Identify the interactions table earth

System Schema block label the interaction types N G table G earth
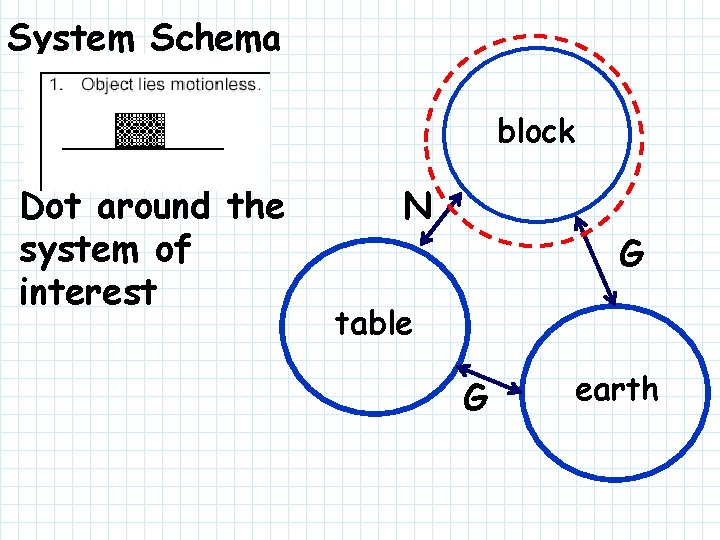
System Schema block Dot around the system of interest N G table G earth
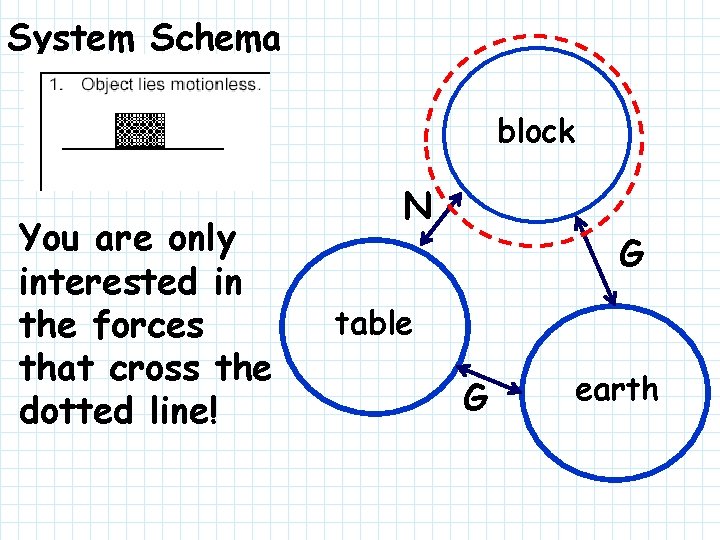
System Schema block You are only interested in the forces that cross the dotted line! N G table G earth

Agent/Object Notation Type of force Object the force acts on. “Feeler” Agent that produces the force. “Dealer” If the agent can't be identified, the force doesn't exist!

Constant Velocity FN T/B block N G table G earth FG E/B

Constant Velocity FN T/B When the object is moving, include a velocity vector off to the side v FG E/B Note: the velocity vector does NOT touch the dot.

Changing velocity FN T/B v block N f Ff T/B G table G earth FG E/B

Changing velocity FN T/B Ff T/B v a FG E/B Note: the acceleration vector does NOT touch the dot.

Non Perpendicular Forces Object slides without friction FN R/B v block N G ramp G earth FG E/B

Non Perpendicular Forces FN Ff Ramp ll/B Another form of A/O notation Components should not appear on the FBD!! Ramp ⊥ /B = FN = f FG E/B= Wt

Unambiguous Force Labeling FT Rope 1/B = T 1 FT FG E/B= Rope 2/B Wt = T 2

Forces – Relative lengths FT FN T⊥/B = FN Ff Tll/B R/B= θ = f v FG E/B = mg T

Ambiguity in HW is OK Ff OR v FG E/B= mg A/B= v D FG E/B= mg

NEWTON'S LAWS FIRST LAW Object at rest or moving with constant velocity. Isaac Newton (1642 -1727) ΣF = 0 (Equilibrium) Vectors should be written in component form: ΣFx = 0 ΣFy = 0

2005 B 2 2005 B 2. A simple pendulum consists of a bob of mass 1. 8 kg attached to a string of length 2. 3 m. The pendulum is held at an angle of 30° from the vertical by a light horizontal string attached to a wall, as shown. a. Draw a free‑body diagram labeling the forces on the bob in the position shown.

FT s 1/B = T 1 FT FG E/B= s 2/B=T 2 mg

b. Calculate the tension in the horizontal string. T 1 60° T 2 ΣFH = T 2 – T 1 cos 60º = 0 ΣFV = T 1 sin 60º - mg = 0 mg T 2 = 10. 18 N

c. The horizontal string is now cut close to the bob, and the pendulum swings down. Calculate the speed of the bob at its lowest position. L h h = L - Lcosθ = 2. 5 m/s

The End (for now)
- Slides: 27