Dynamics Acceleration and VelocityTime Graphs Acceleration Success Criteria

Dynamics Acceleration and Velocity-Time Graphs

Acceleration Success Criteria By the end of the lesson, you should be able to:

Definition The acceleration of an object is the change in velocity per second. An acceleration of 5 ms-2 means the velocity increases by 5 ms-1 , every second. An acceleration of 9· 8 ms-2 means the velocity increases by 9· 8 ms-1, every second.

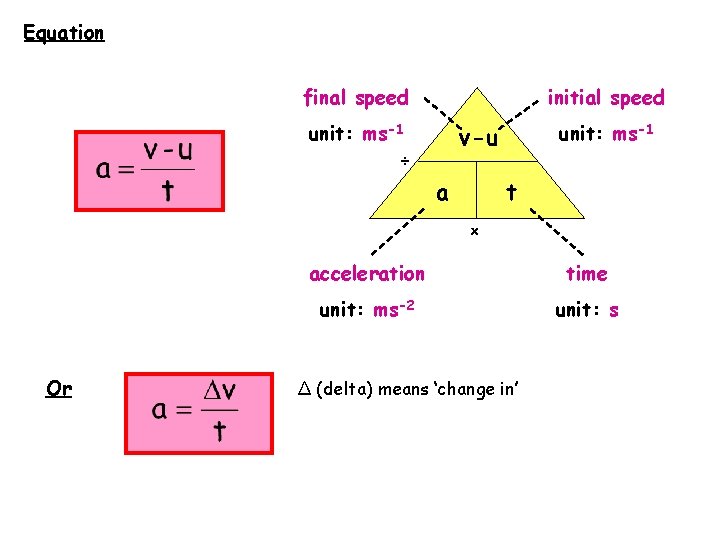
Equation final speed initial speed unit: ms-1 v-u ÷ a t x Or acceleration time unit: ms-2 unit: s Δ (delta) means ‘change in’

Equation for Final Velocity Re-arrange the acceleration equation: ** NOT on data sheet **

Example 1 A car accelerates from a speed of 5 ms-1 to a speed of 15 ms-1 in a time of 2. 5 seconds. Calculate the car’s acceleration.

Example 2 A digger’s speed changes from 9 ms-1 to a speed of 2 ms-1 in 1· 5 s. Calculate the digger’s acceleration. Deceleration is always negative.

Tutorial 3 – Acceleration and Deceleration Calculations 1. Farmer Jones’ tractor starts from rest and speeds up to 8 ms-1 in 10 s. Calculate the acceleration of the tractor. 2. Jill and her mum’s go-kart moves from rest and reaches a final speed of 6 ms-1 in a time of 12 s. Calculate the acceleration of the go-kart. 3. Sue and Tom’s golfing car accelerates from 2 ms-1 to 9 ms-1 in 5 s. Calculate the acceleration of their buggy.

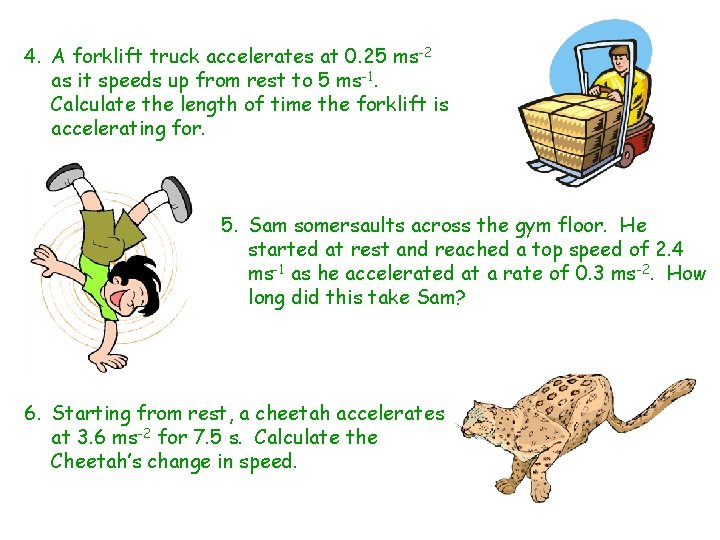
4. A forklift truck accelerates at 0. 25 ms-2 as it speeds up from rest to 5 ms-1. Calculate the length of time the forklift is accelerating for. 5. Sam somersaults across the gym floor. He started at rest and reached a top speed of 2. 4 ms-1 as he accelerated at a rate of 0. 3 ms-2. How long did this take Sam? 6. Starting from rest, a cheetah accelerates at 3. 6 ms-2 for 7. 5 s. Calculate the Cheetah’s change in speed.

7. A fireman initially at rest, slides down a pole with an acceleration of 1. 2 ms-2. His speed at the bottom of the pole is 3. 6 ms-1. Calculate the time taken to slide down the pole. 8. When a stationary rugby ball is kicked, it is contact with the player’s boot for 0. 05 s. During this short time the ball accelerates at 600 ms-2. Calculate the speed at which the ball leaves the player’s foot. 9. A helicopter flying at 35 ms-1 decelerates for 12 s at a rate of 2. 5 ms-2. Calculate the final speed of the helicopter.

10. The speed of a conveyor belt is increased to 2. 8 ms-1 by accelerating at 0. 3 ms-2 for 4 s. Calculate the initial speed of the conveyor belt. 11. A bee decelerating at 0. 7 ms-2 slows down from 6. 7 ms-1 to 2. 5 ms-1. Calculate how long this will take. 12. A van decelerating at a rate of 1. 4 ms-2 does so for 5 s. As a result, its speed reduces to 24 ms-1. Calculate the van’s initial speed.

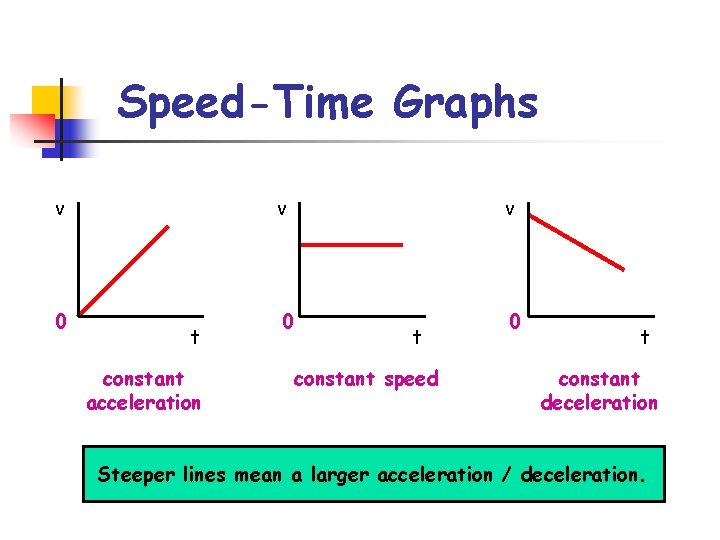
Speed-Time Graphs v 0 v t constant acceleration v 0 t constant speed 0 t constant deceleration Steeper lines mean a larger acceleration / deceleration.

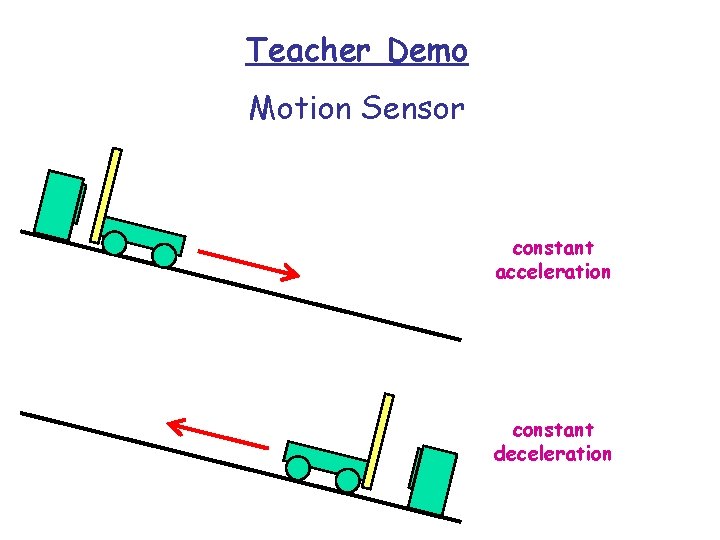
Teacher Demo Motion Sensor constant acceleration constant deceleration

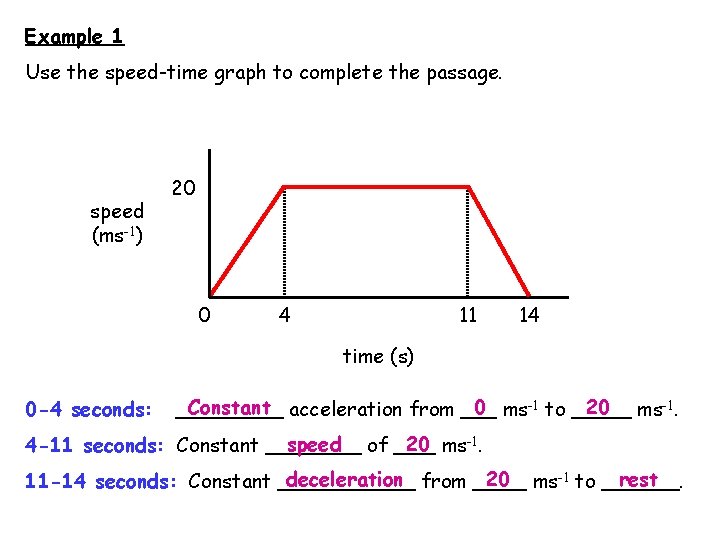
Example 1 Use the speed-time graph to complete the passage. speed (ms-1) 20 0 11 4 14 time (s) 0 -4 seconds: Constant acceleration from 0 ms-1 to 4 -11 seconds: Constant speed 20 ms-1. of 20 ms-1. 11 -14 seconds: Constant deceleration from 20 ms-1 to rest .

Calculations and Speed-Time Graphs Taking the initial speed, final speed and time values from a speed time graph, the acceleration can be calculated. The acceleration is calculated using:

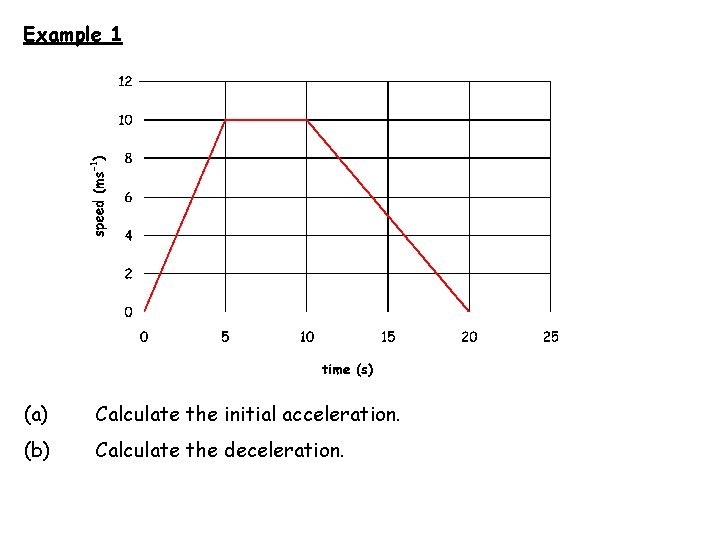
Example 1 (a) Calculate the initial acceleration. (b) Calculate the deceleration.

(a) Calculate the initial acceleration. (b) Calculate the deceleration.

Nat 5 Problem Booklet Graphs – Page 10 Q 3

Total Distance Travelled The total distance travelled can be calculated from a speed-time graph. total distance = travelled area under the speed-time graph *** NOT on relationship sheet *** Split the speed-time graph into common shapes and calculate the total area under the speed-time graph.

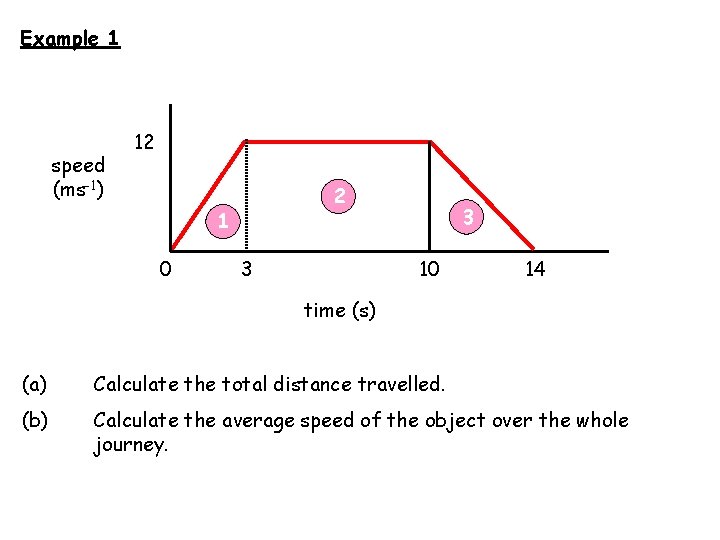
Example 1 speed (ms-1) 12 2 1 0 3 14 time (s) (a) Calculate the total distance travelled. (b) Calculate the average speed of the object over the whole journey.

(a) Calculate the total distance travelled. Total Distance = Area Under Graph = Area 1 + Area 2 + Area 3 Area 1 Area 2 The total distance travelled is: Area 3

(b) Calculate the average speed of the object over the whole journey.

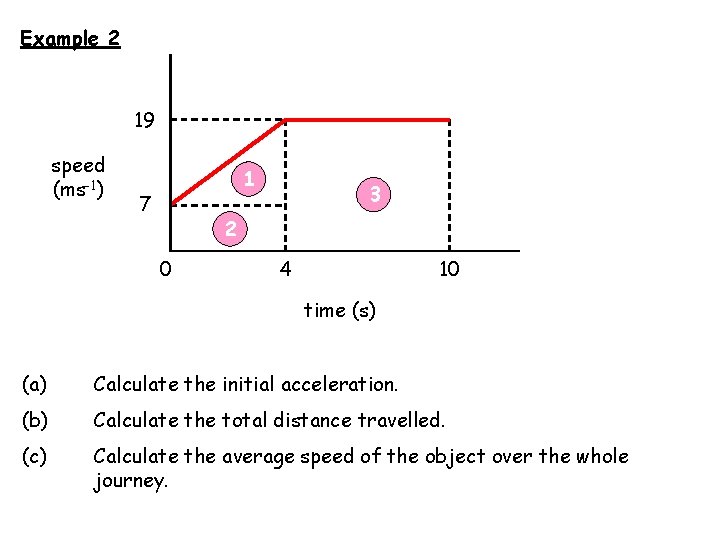
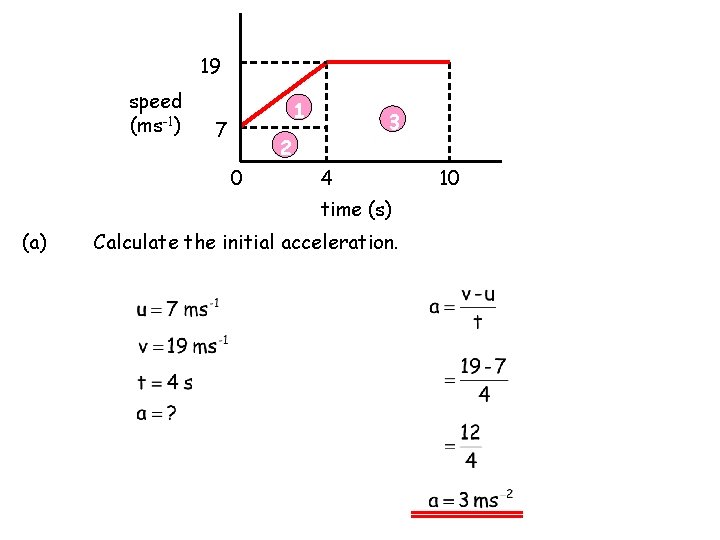
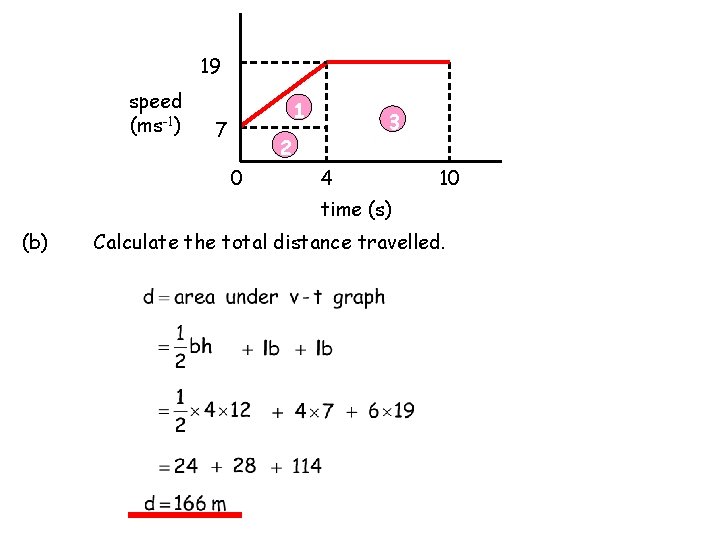
Example 2 19 speed (ms-1) 1 7 3 2 0 10 4 time (s) (a) Calculate the initial acceleration. (b) Calculate the total distance travelled. (c) Calculate the average speed of the object over the whole journey.

19 speed (ms-1) 1 7 3 2 0 4 time (s) (a) Calculate the initial acceleration. 10

19 speed (ms-1) 1 7 3 2 0 4 10 time (s) (b) Calculate the total distance travelled.

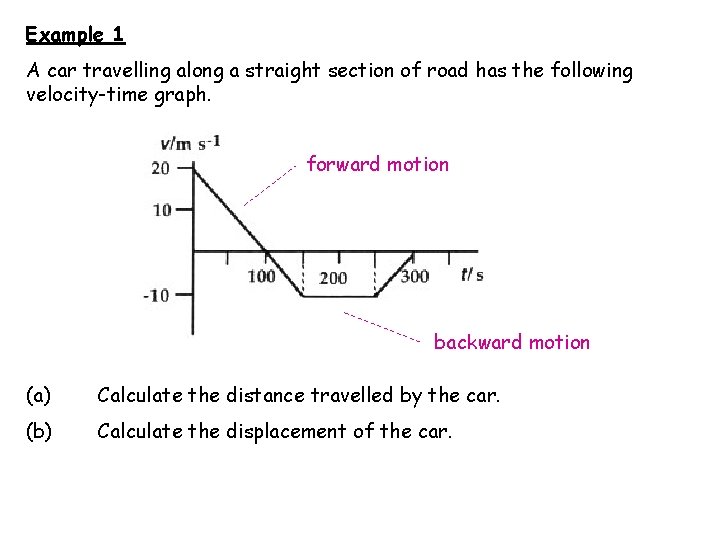
Example 1 A car travelling along a straight section of road has the following velocity-time graph. forward motion backward motion (a) Calculate the distance travelled by the car. (b) Calculate the displacement of the car.

(a) Distance travelled is the area under velocity-time graph. (b) Displacement is the forwards motion, less the backward motion. (500 m backwards)