Dynamical Localization and Delocalization in a Quasiperiodic Driven

Dynamical Localization and Delocalization in a Quasiperiodic Driven System Hans Lignier, Jean Claude Garreau, Pascal Szriftgiser Laboratoire de Physique des Lasers, Atomes et Molécules, PHLAM, Lille, France Dominique Delande Laboratoire Kastler-Brossel, Paris, France FRISNO-8, EIN BOKEK 2005 This work has been supported by :

The Quantum Chaos Project: - An experimental realization of an atomic kicked rotor -The observation of the « Dynamical Localization » Phenomenon, and its destruction induced by time periodicity breaking - Observation of sub-Fourier resonances - Is DL’s destruction reversible?

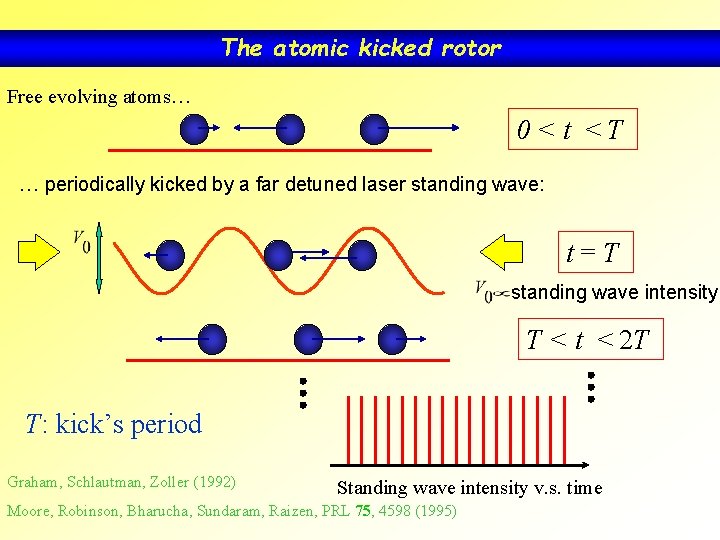
The atomic kicked rotor Free evolving atoms… 0<t <T … periodically kicked by a far detuned laser standing wave: t=T standing wave intensity T < t < 2 T T: kick’s period Graham, Schlautman, Zoller (1992) Standing wave intensity v. s. time Moore, Robinson, Bharucha, Sundaram, Raizen, PRL 75, 4598 (1995)

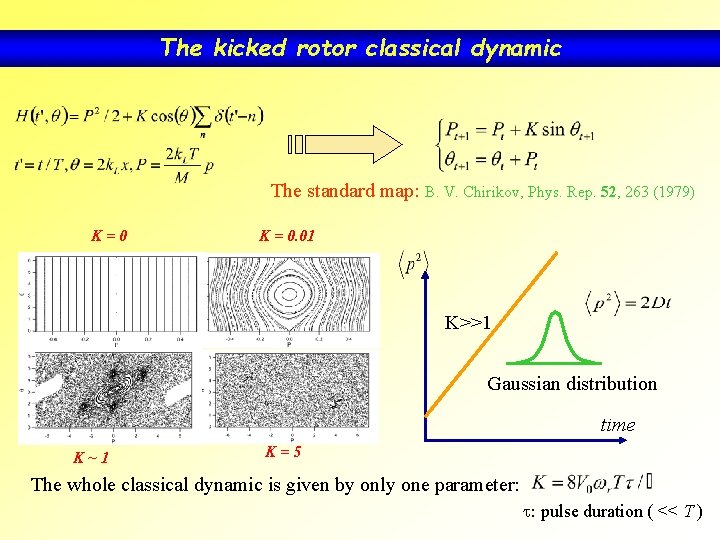
The kicked rotor classical dynamic The standard map: B. V. Chirikov, Phys. Rep. 52, 263 (1979) K=0 K = 0. 01 K>>1 Gaussian distribution time K~1 K=5 The whole classical dynamic is given by only one parameter: t: pulse duration ( << T )

Quantized standard map Same Hamiltonian: Schrödinger equation: scaled Planck constant Two parameters: k and K Quantization of the map:

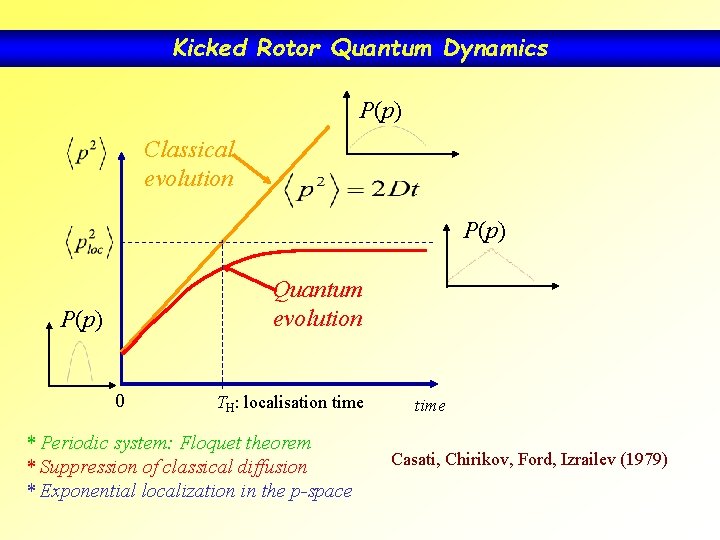
Kicked Rotor Quantum Dynamics P(p) Classical evolution P(p) Quantum evolution P(p) 0 TH: localisation time * Periodic system: Floquet theorem * Suppression of classical diffusion * Exponential localization in the p-space time Casati, Chirikov, Ford, Izrailev (1979)

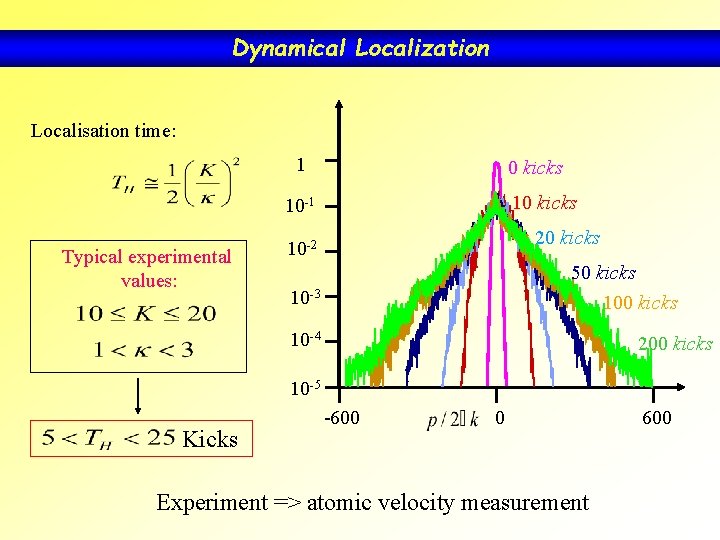
Dynamical Localization Localisation time: 1 0 kicks 10 -1 Typical experimental values: 20 kicks 10 -2 50 kicks 10 -3 100 kicks 10 -4 200 kicks 10 -5 Kicks -600 0 Experiment => atomic velocity measurement 600

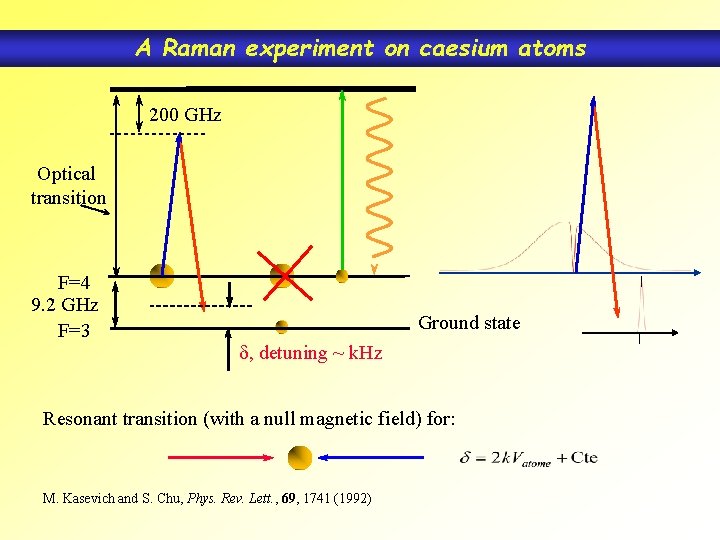
A Raman experiment on caesium atoms 200 GHz Optical transition F=4 9. 2 GHz F=3 Ground state d, detuning ~ k. Hz Resonant transition (with a null magnetic field) for: M. Kasevich and S. Chu, Phys. Rev. Lett. , 69, 1741 (1992)

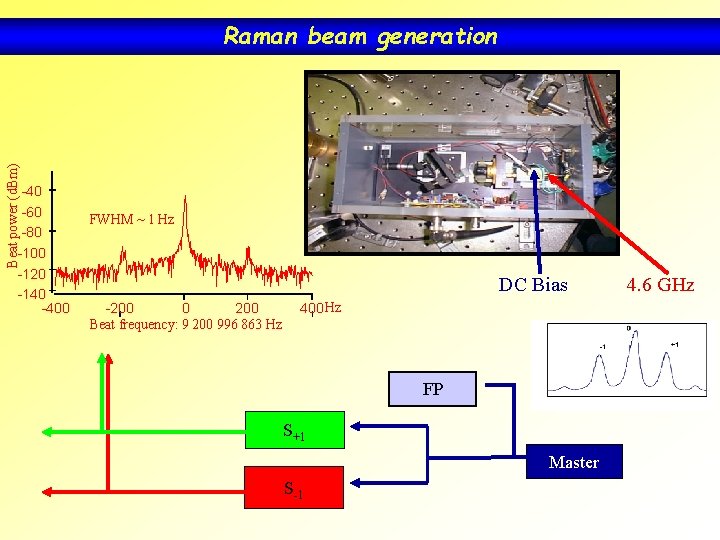
Beat power (d. Bm) Raman beam generation -40 -60 -80 -100 -120 -140 -400 FWHM ~ 1 Hz DC Bias -200 0 200 Beat frequency: 9 200 996 863 Hz 400 Hz FP S+1 Master S-1 4. 6 GHz

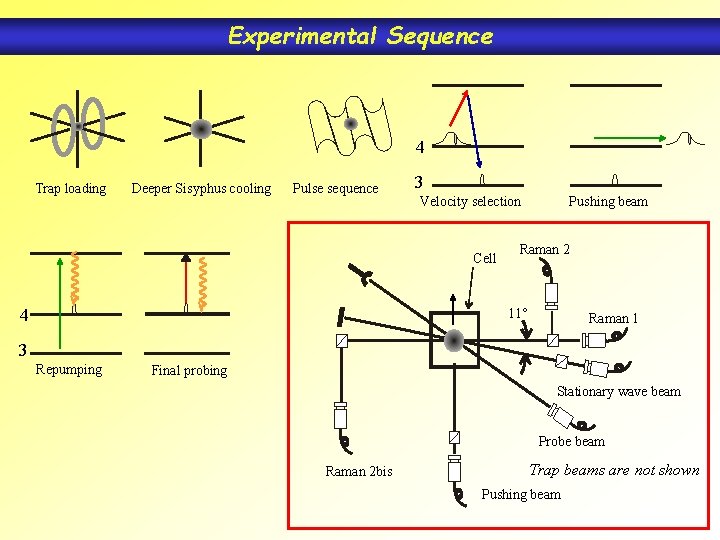
Experimental Sequence 4 Trap loading Deeper Sisyphus cooling Pulse sequence 3 Velocity selection Cell 4 Pushing beam Raman 2 11° Raman 1 3 Repumping Final probing Stationary wave beam Probe beam Raman 2 bis Trap beams are not shown Pushing beam

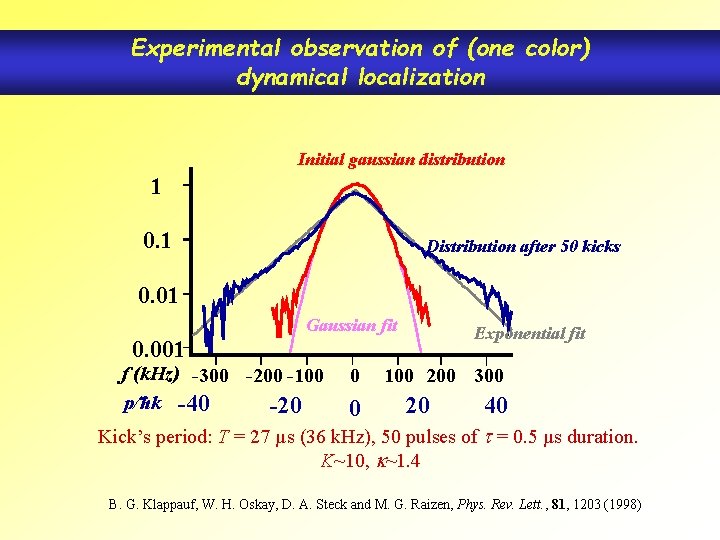
Experimental observation of (one color) dynamical localization Initial gaussian distribution 1 0. 1 Distribution after 50 kicks 0. 01 Gaussian fit Exponential fit 0. 001 f (k. Hz) -300 -200 -100 p/hk -40 -20 0 0 100 200 300 20 40 Kick’s period: T = 27 µs (36 k. Hz), 50 pulses of t = 0. 5 µs duration. K~10, k~1. 4 B. G. Klappauf, W. H. Oskay, D. A. Steck and M. G. Raizen, Phys. Rev. Lett. , 81, 1203 (1998)

Two colours modulation One colour modulation : Two colours modulation : r = f 1/f 2, frequency ratio of two pulse series: f 1 f 2 time -Periodicity breaking and Floquet’s states. -Relationship between frequency modulation and effective dimensionality. -Dynamical localisation and Anderson localisation. G. Casati, I. Guarneri and D. L. Shepelyansky, Phys. Rev. Lett. , 62, 345 (1989)

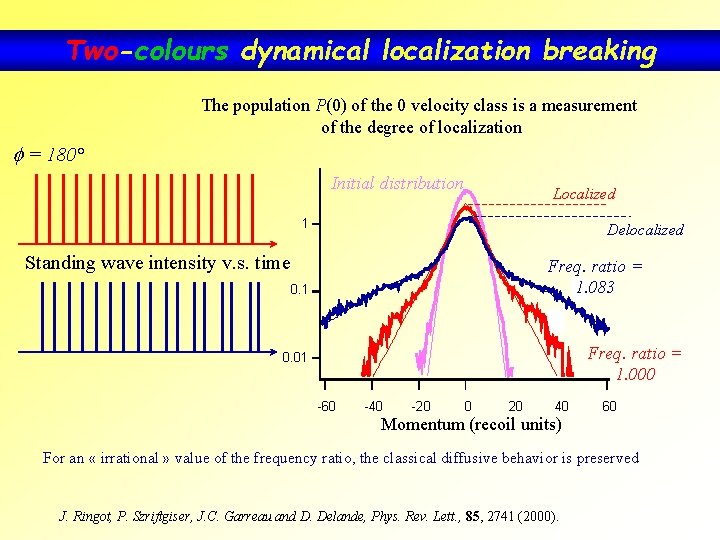
Two-colours dynamical localization breaking The population P(0) of the 0 velocity class is a measurement of the degree of localization f = 180° Initial distribution Localized 1 Delocalized Standing wave intensity v. s. time Freq. ratio = 1. 083 0. 1 Freq. ratio = 1. 000 0. 01 -60 -40 -20 0 20 40 Momentum (recoil units) 60 For an « irrational » value of the frequency ratio, the classical diffusive behavior is preserved J. Ringot, P. Szriftgiser, J. C. Garreau and D. Delande, Phys. Rev. Lett. , 85, 2741 (2000).

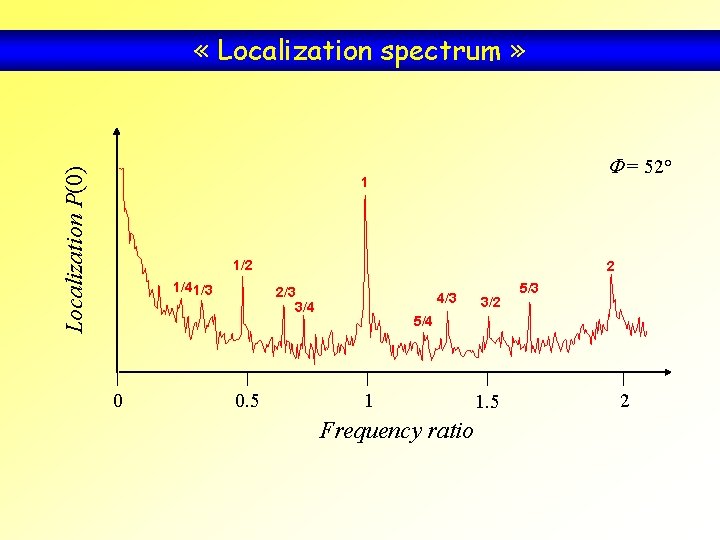
Localization P(0) « Localization spectrum » F = 52° 1 1/2 1/4 1/3 0 2 2/3 3/4 0. 5 4/3 3/2 5/3 5/4 1 Frequency ratio 1. 5 2

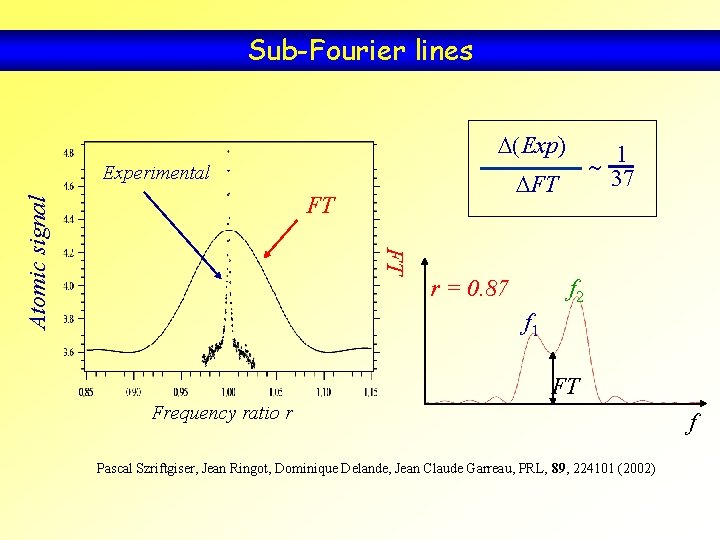
Sub-Fourier lines D(Exp) Experimental DFT FT FT Atomic signal ~ 1 37 r = 0. 87 f 2 f 1 FT Frequency ratio r Pascal Szriftgiser, Jean Ringot, Dominique Delande, Jean Claude Garreau, PRL, 89, 224101 (2002) f

First Interpretation The higher harmonics in the excitation spectrum are responsible of the higher resolution: Þ (1) The resonance’s width is independent of the kick’s strength K Þ (2) If the pulse width is increased => the resonance’s width should increase as well Þ (3) The resonance’s width decay as 1/Texcitation sequence Experimental points at N 1=10, for t = 1, 2, 3 µs Assuming: Resonance width ×N 1 Fourier limit 1 µs 2 µs 3 µs K = 14 K = 28 K = 42 Pulse number N 1 Numerical evaluation of the resonance’s width as a function of time. The resonance width shrinks faster than the reciprocal length of the excitation time

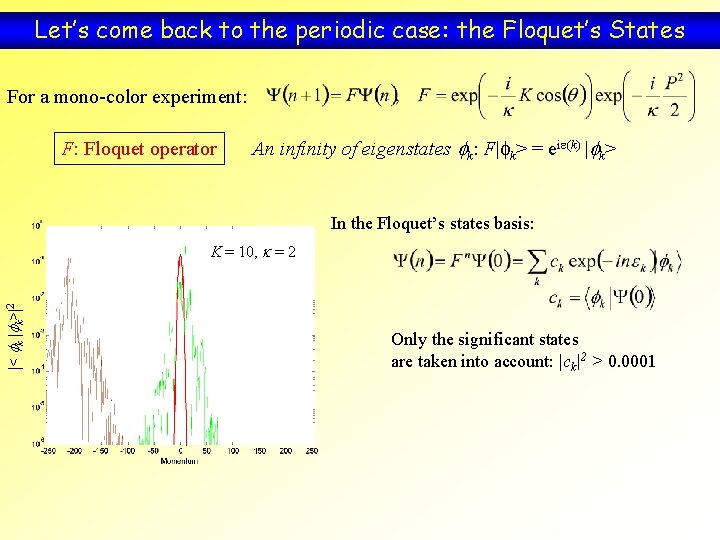
Let’s come back to the periodic case: the Floquet’s States For a mono-color experiment: F: Floquet operator An infinity of eigenstates fk: F|fk> = eie(k) |fk> In the Floquet’s states basis: |< fk |fk>|2 K = 10, k = 2 Only the significant states are taken into account: |ck|2 > 0. 0001

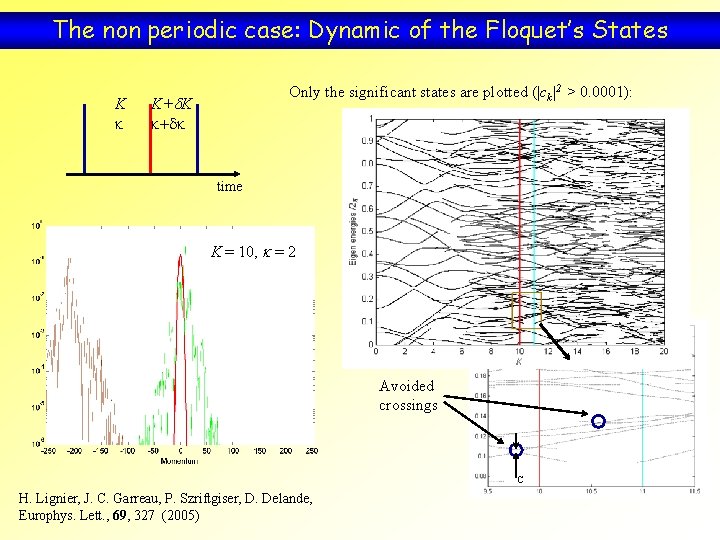
The non periodic case: Dynamic of the Floquet’s States K k Only the significant states are plotted (|ck|2 > 0. 0001): K+d. K k+dk time K = 10, k = 2 Avoided crossings C H. Lignier, J. C. Garreau, P. Szriftgiser, D. Delande, Europhys. Lett. , 69, 327 (2005)

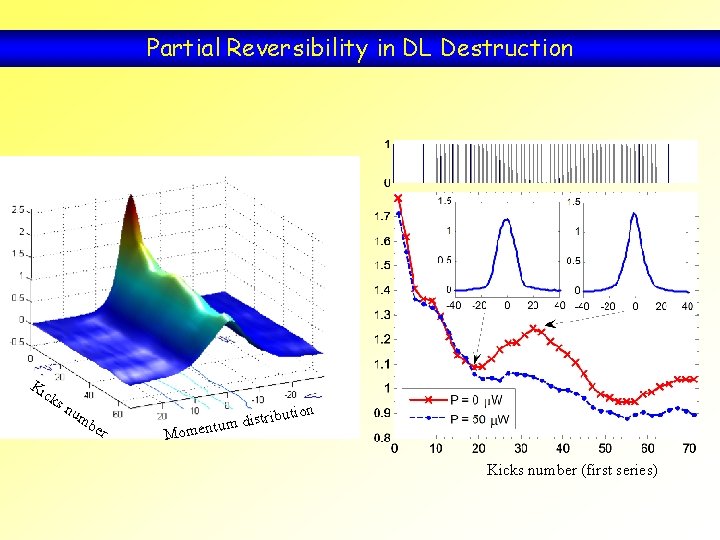
Partial Reversibility in DL Destruction Ki ck sn tion um be r stribu i d m u t omen M Kicks number (first series)

Conclusion Dynamical localization destruction Complex dynamics – unexpected results Observation of a partial reconstruction of DL

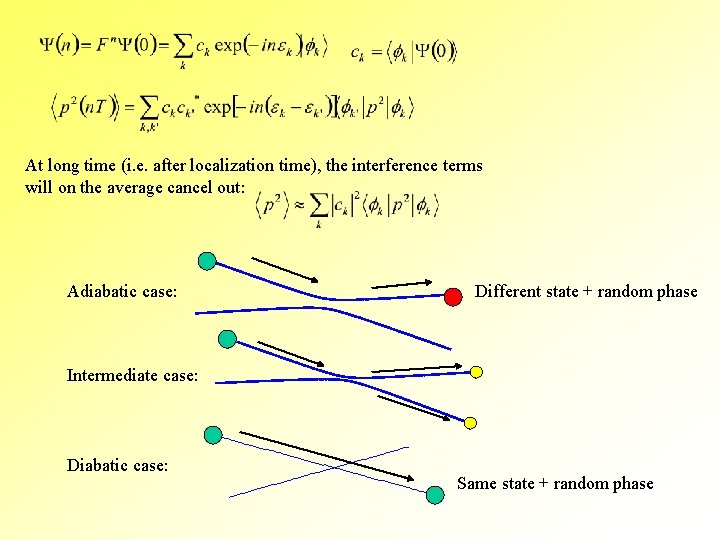
At long time (i. e. after localization time), the interference terms will on the average cancel out: Adiabatic case: Different state + random phase Intermediate case: Diabatic case: Same state + random phase