Dynamic Thread Mapping for High Performance PowerEfficient Heterogeneous

Dynamic Thread Mapping for High. Performance, Power-Efficient Heterogeneous Many-core Systems Guangshuo Liu Jinpyo Park Diana Marculescu Presented By Ravi Teja Arrabolu (vxa 132930)

Introduction • The problem of dynamic thread mapping in heterogeneous many-core systems is addressed via an efficient algorithm that maximizes performance under power constraints. Heterogeneous many-core systems are composed of multiple core types with different power-performance characteristics. • This paper proposes an iterative approach bounding the runtime as O(n 2/m) , for mapping multi-threaded applications on n cores comprising of m core types

Heterogeneous Core Types • A core type is defined by a tuple of microarchitecture features and associated nominal voltage/frequency. • For example, cores that differ in architectural parameters, such as issue width, cache size, number of function units, etc. , are considered as different core types. • In addition, even if two cores are designed identically in terms of microarchitecture but associated with different nominal frequencies, they are considered as distinct core types.

General Notations • The throughput matrix is denoted by T ∈ Rn×m. Each element Tij represents the throughput of thread i running on a core in type j. Throughput is defined as the total number of instructions committed per unit of time. • The power matrix is denoted by P ∈ Rn×m. Each element Pij represents the total power consumption for thread i running on a core in type j. • The assignment matrix X ∈ {0, 1}n×m represents the assignment of threads to each core type. Thread i is mapped to core type j if and only if Xij = 1.

Constraints • Objective function: Maximize performance defined by the total throughput, maximize ∑i, j Tij. Xij • First, the power budget needs to be satisfied, ∑i, j Pij. Xij ≤ total TDP of cores. • Second, a thread can be only mapped to a single core, ∀i : ∑j Xij ≤ 1. • The core count in each type is given, ∀j : ∑i Xij ≤ core countj. • Finally, the mapping is a 0 -1 assignment problem, and therefore ∀i, j : ∑i, j Xij ∈ {0, 1}.

Experiment Setup • Sniper multi-core simulator was used to conduct the simulation tests. • Sniper provides support of heterogeneous configurations and dynamic thread migration. • It employs Mc. PAT as the power estimation engine. • All the L 1 and L 2 caches are private to cores and there is no L 3 cache. • For the cases in which the number of cores of each type is identical, the network hierarchy is configured as a mesh of tiles. • If the core count is different in each type, we will have some tiles with fewer core types.

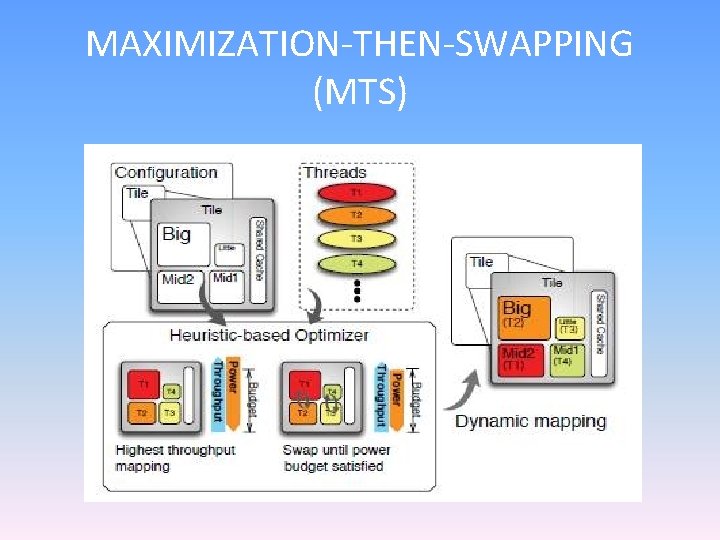
MAXIMIZATION-THEN-SWAPPING (MTS)

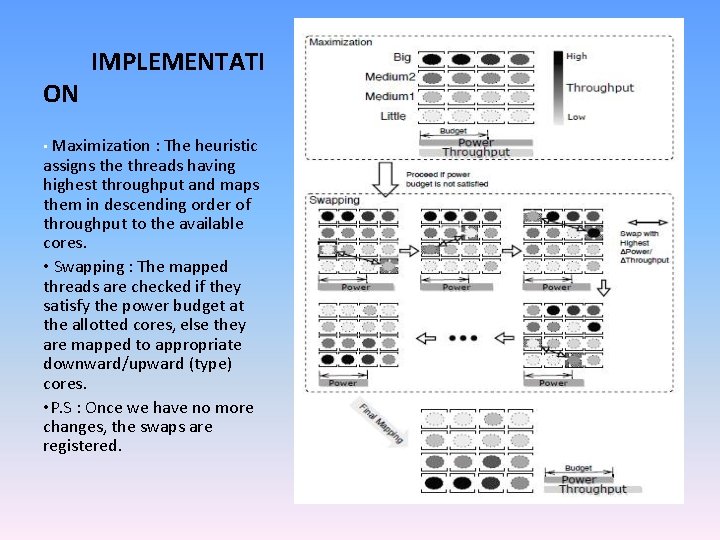
ON IMPLEMENTATI • Maximization : The heuristic assigns the threads having highest throughput and maps them in descending order of throughput to the available cores. • Swapping : The mapped threads are checked if they satisfy the power budget at the allotted cores, else they are mapped to appropriate downward/upward (type) cores. • P. S : Once we have no more changes, the swaps are registered.

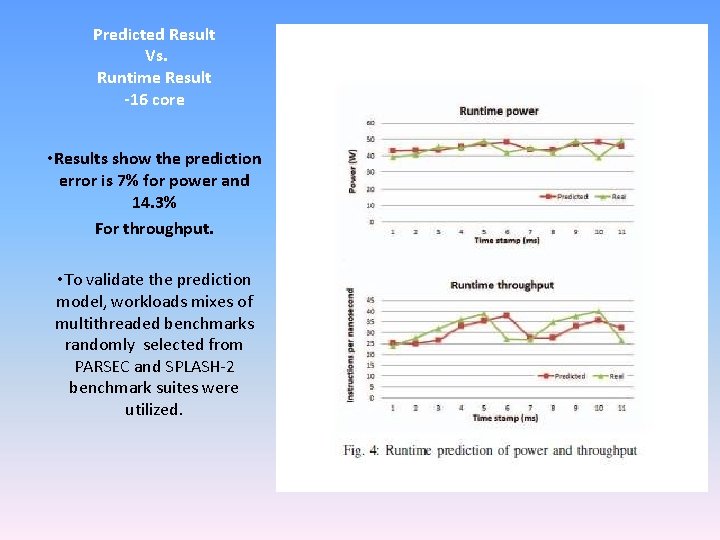
Predicted Result Vs. Runtime Result -16 core • Results show the prediction error is 7% for power and 14. 3% For throughput. • To validate the prediction model, workloads mixes of multithreaded benchmarks randomly selected from PARSEC and SPLASH-2 benchmark suites were utilized.

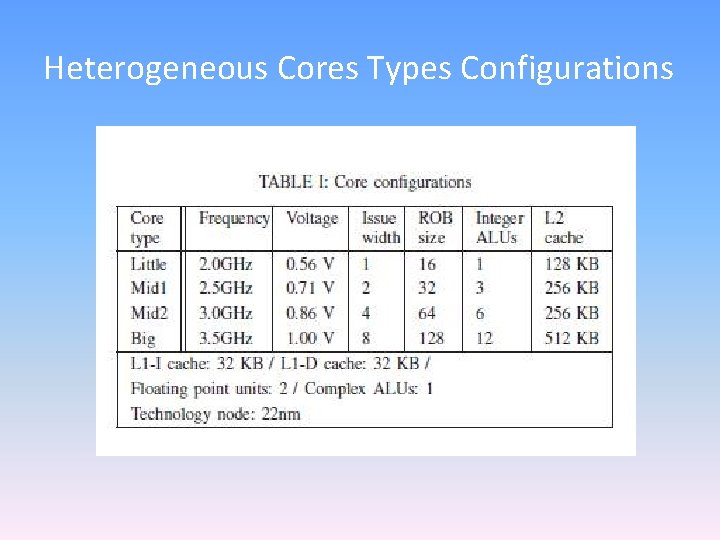
Heterogeneous Cores Types Configurations

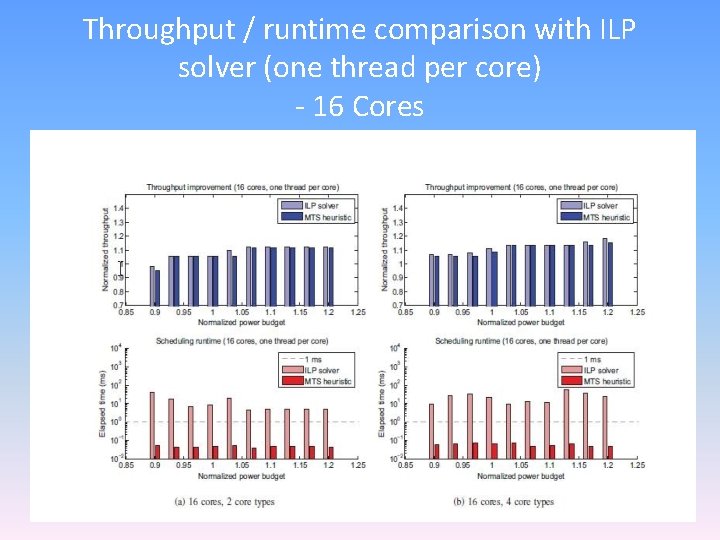
Throughput / runtime comparison with ILP solver (one thread per core) - 16 Cores

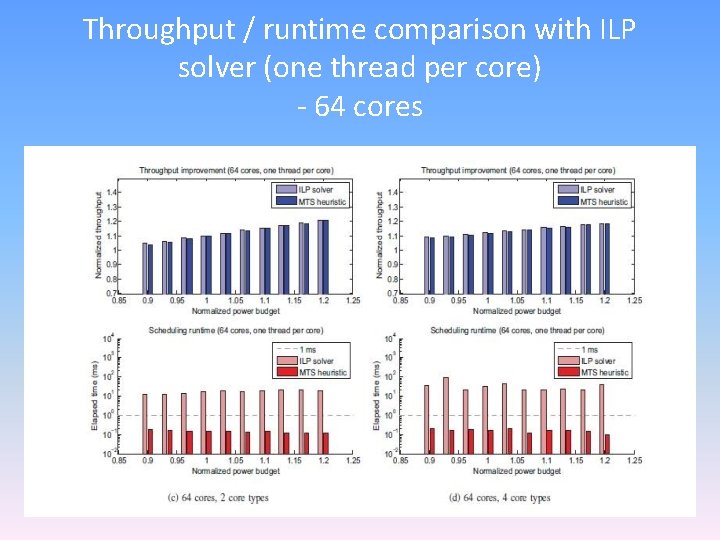
Throughput / runtime comparison with ILP solver (one thread per core) - 64 cores

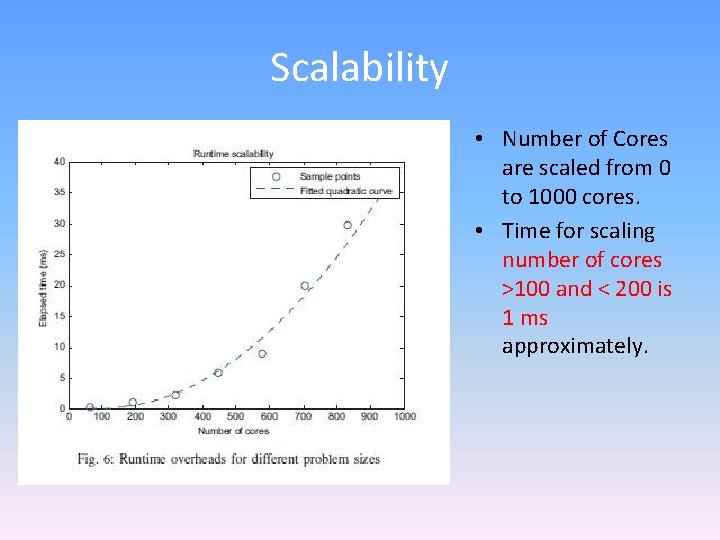
Scalability • Number of Cores are scaled from 0 to 1000 cores. • Time for scaling number of cores >100 and < 200 is 1 ms approximately.

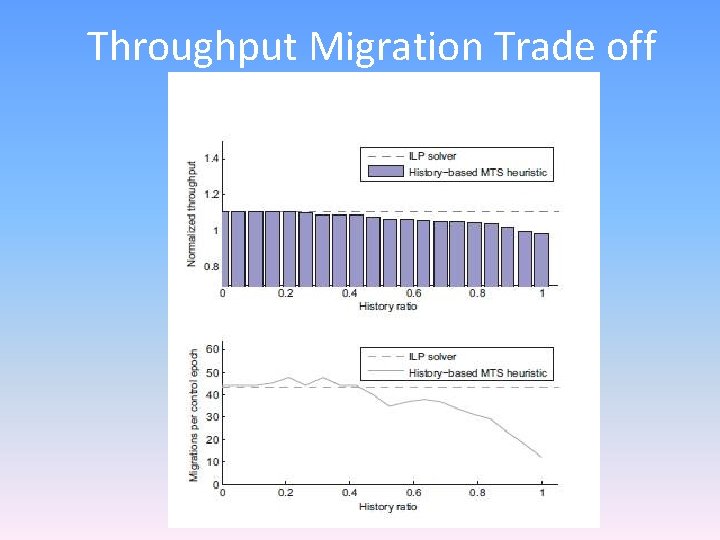
History Based MTS • To minimize migration cost, we further enable MTS heuristic to take the original mapping (history) into account. • history ratio is introduced, which ranges from 0 to 1 • the number of threads that are considered in the maximization phase is limited to n×(1−history ratio). • As history ratio increases, the migration cost can be reduced since fewer threads will be migrated between the original mapping and the final one.

Throughput Migration Trade off

Limitations • Load Balancing, No Simultaneous Multi threading The paper confines to single thread per core which limits task migration between cores, which implies that sharing the threads is not considered, resulting in some tasks may miss deadlines. • Fairness The paper does not consider each process's priority and workloads, but assigns the process to the cores depending on their types, which can result in CPU utilization loss, also effecting the Qo. S of such real time applications.