Dynamic System Modeling using Reliability Graph with General

Dynamic System Modeling using Reliability Graph with General Gates Lab Seminar Jan. 8 th, 2007 Seung Ki, Shin

Contents § Introduction § Two Types of Dynamic Fault Trees § Dynamic System modeling using RGGG (Reliability Graph with General Gates) § Quantification Example § Practical Application § Summary & Further Study § References Korea Advanced Institute of Science and Technology 1

Introduction § Dynamic fault tree is a time-dependent fault tree, so it can capture the dynamic behavior of the system failure mechanisms. § Dynamic properties of the system failure mechanisms can be divided into two types, so there exist two types of dynamic fault trees. § One type of dynamic failure mechanisms can be analyzed using RGGG. Korea Advanced Institute of Science and Technology 2

Two Types of Dynamic Fault Trees § Two types of dynamic failure mechanisms § Failure mechanism composed of sequence-dependent events § Failure mechanism of which configuration changes with time § Dynamic fault tree involving dynamic gates § It can model the failure mechanism composed of sequence-dependent events. § PAND (Priority-AND) , SEQ (Sequence Enforcing), FDEP (Functional Dependency), SPARE gates Korea Advanced Institute of Science and Technology 3

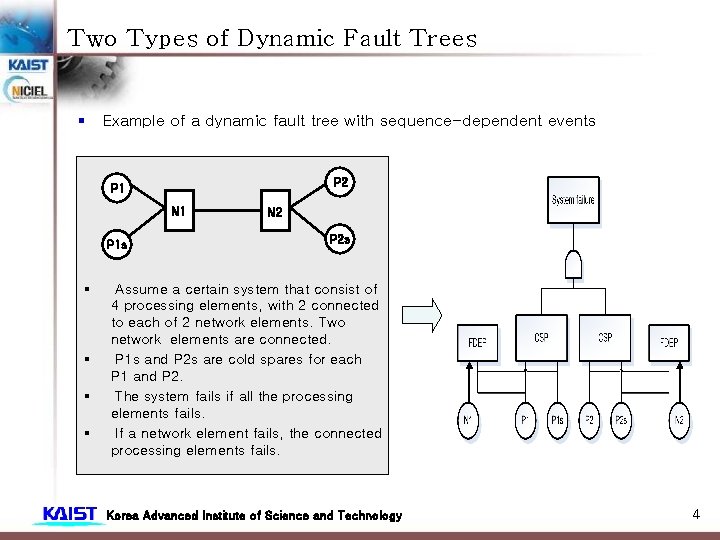
Two Types of Dynamic Fault Trees § Example of a dynamic fault tree with sequence-dependent events P 2 P 1 N 1 P 1 s § § N 2 P 2 s Assume a certain system that consist of 4 processing elements, with 2 connected to each of 2 network elements. Two network elements are connected. P 1 s and P 2 s are cold spares for each P 1 and P 2. The system fails if all the processing elements fails. If a network element fails, the connected processing elements fails. Korea Advanced Institute of Science and Technology 4

Two Types of Dynamic Fault Trees § Dynamic fault tree involving house events § It can model the failure mechanism whose configuration changes with time. § One fault tree can represent various configuration using house events. § House events are used to switch on and off respective parts of the integrated fault tree. Korea Advanced Institute of Science and Technology 5

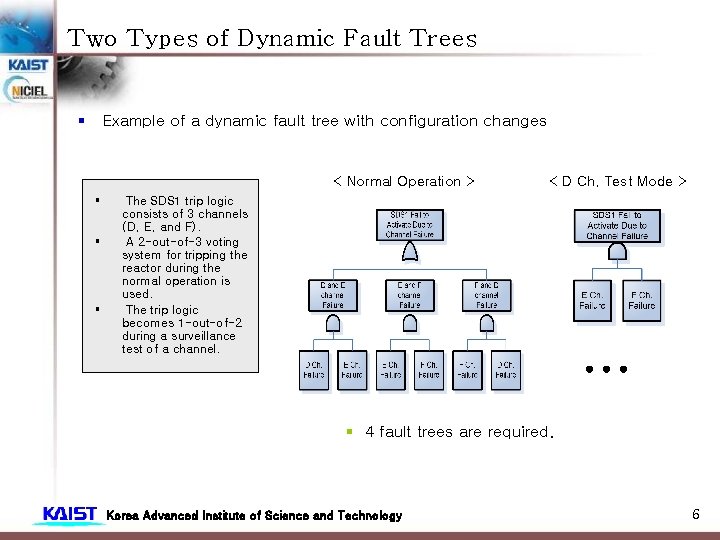
Two Types of Dynamic Fault Trees § Example of a dynamic fault tree with configuration changes < Normal Operation > § § § < D Ch. Test Mode > The SDS 1 trip logic consists of 3 channels (D, E, and F). A 2 -out-of-3 voting system for tripping the reactor during the normal operation is used. The trip logic becomes 1 -out-of-2 during a surveillance test of a channel. § 4 fault trees are required. Korea Advanced Institute of Science and Technology 6

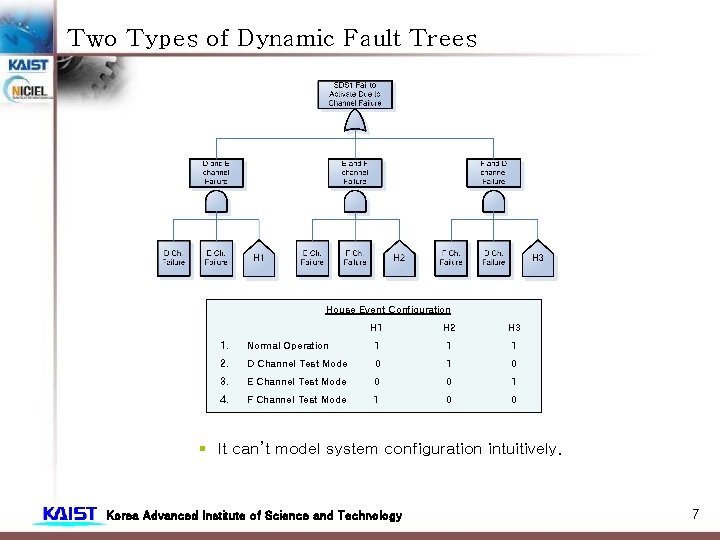
Two Types of Dynamic Fault Trees House Event Configuration H 1 H 2 H 3 1. Normal Operation 1 1 1 2. D Channel Test Mode 0 1 0 3. E Channel Test Mode 0 0 1 4. F Channel Test Mode 1 0 0 § It can’t model system configuration intuitively. Korea Advanced Institute of Science and Technology 7

Analysis of Dynamic System using RGGG § Reliability Graph § There exist various methods for system reliability analysis. § Reliability graph, Markov Chain, Fault tree analysis, Monte Carlo simulation § For a method for system reliability analysis to be intuitive, one of the most important things is the one-to-one match between the actual structure of a system and the model for the system. § A reliability graph is composed of nodes and arcs. § Node : Component in a system § Arc : Link between two components § Reliability graph is the most intuitive method to analyze the reliability of a system. Korea Advanced Institute of Science and Technology 8

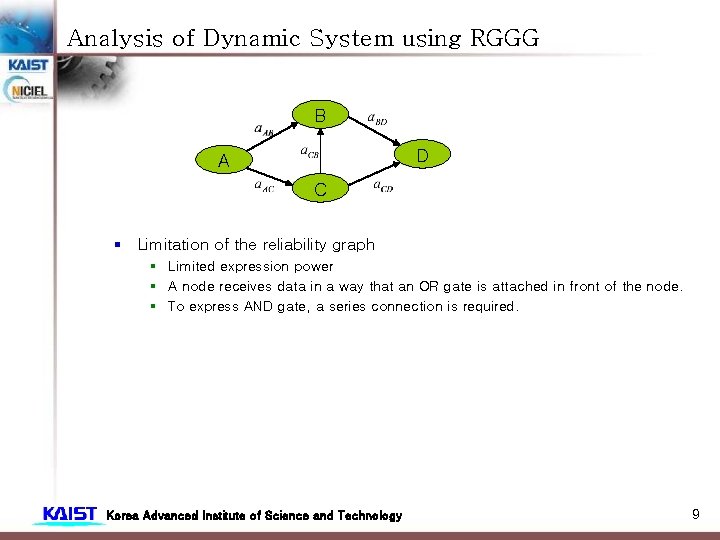
Analysis of Dynamic System using RGGG B D A C § Limitation of the reliability graph § Limited expression power § A node receives data in a way that an OR gate is attached in front of the node. § To express AND gate, a series connection is required. Korea Advanced Institute of Science and Technology 9

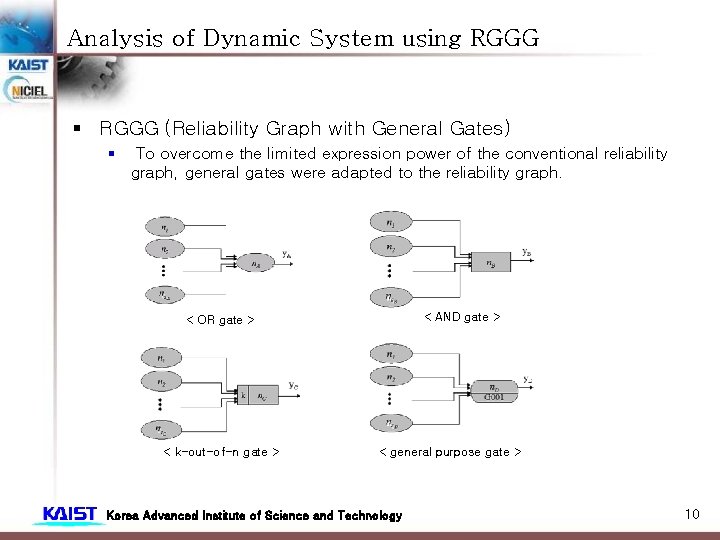
Analysis of Dynamic System using RGGG § RGGG (Reliability Graph with General Gates) § To overcome the limited expression power of the conventional reliability graph, general gates were adapted to the reliability graph. < AND gate > < OR gate > < k-out-of-n gate > < general purpose gate > Korea Advanced Institute of Science and Technology 10

Analysis of Dynamic System using RGGG § In order to transform RGGG to an equivalent Bayesian network, the probability table for each node should be determined. § OR gate § AND gate § K-out-of-n gate Korea Advanced Institute of Science and Technology 11

Analysis of Dynamic System using RGGG § Analysis of dynamic system using RGGG § Configuration change, one of the dynamic properties can be modeled using RGGG. § Procedure of calculating dynamic system unavailability § § Draw RGGG of system under normal operation. During the surveillance test of a certain component, let the reliability of appropriate arc be 0. § Make ‘reliability change table’ like the house event configuration table of dynamic fault tree. § Calculate the unavailability of each configuration, and derive unavailability of system regarding to each configuration time. Korea Advanced Institute of Science and Technology 12

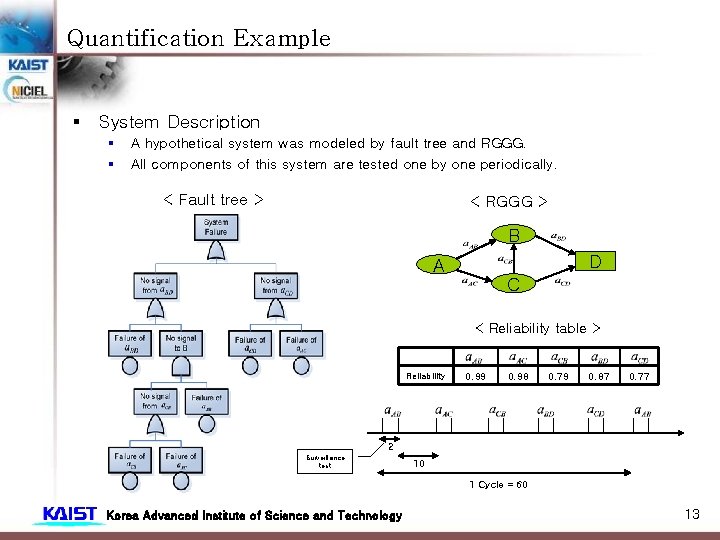
Quantification Example § System Description § § A hypothetical system was modeled by fault tree and RGGG. All components of this system are tested one by one periodically. < Fault tree > < RGGG > B D A C < Reliability table > Reliability 0. 99 0. 98 0. 79 0. 87 0. 77 2 Surveillance test 10 1 Cycle = 60 Korea Advanced Institute of Science and Technology 13

Quantification Example § Unavailability evaluation § Dynamic fault tree method < House event configuration > H_ab H_ac H_cb H_bd H_cd Normal operation 0 0 0 test 1 0 0 test 0 1 0 0 0 test 0 0 1 0 0 test 0 0 0 1 0 test 0 0 1 - Based on the minimal cutsets of each configuration, we can calculate unavailability of each configuration. - Then, derive system unavailability through following equation. Korea Advanced Institute of Science and Technology 14

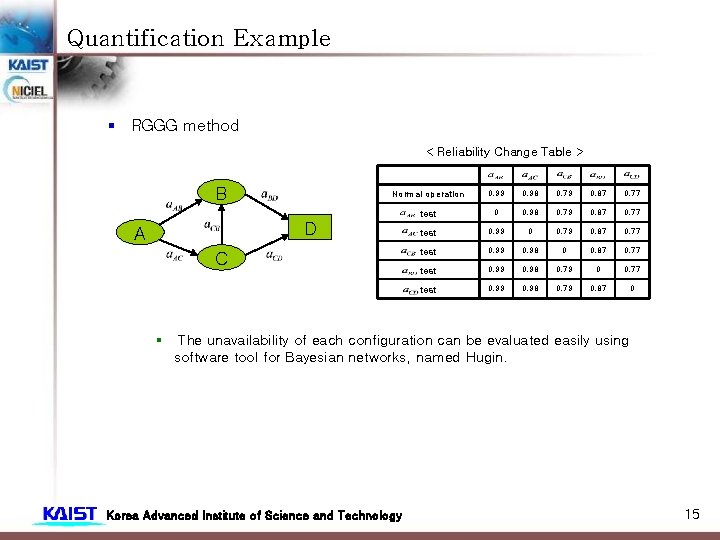
Quantification Example § RGGG method < Reliability Change Table > B Normal operation 0. 99 0. 98 0. 79 0. 87 0. 77 test 0. 99 0. 98 0. 79 0 0. 77 test 0. 99 0. 98 0. 79 0. 87 0 D A C § The unavailability of each configuration can be evaluated easily using software tool for Bayesian networks, named Hugin. Korea Advanced Institute of Science and Technology 15

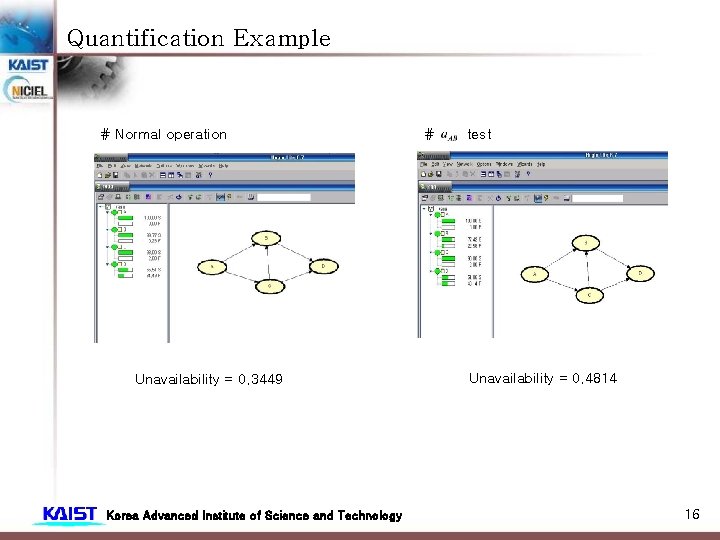
Quantification Example # Normal operation Unavailability = 0. 3449 Korea Advanced Institute of Science and Technology # test Unavailability = 0. 4814 16

Quantification Example < Result table > Unavailability Time 0. 3449 50 test 0. 4814 2 test 1 2 test 0. 3501 2 test 1 2 Normal operation Korea Advanced Institute of Science and Technology 17

Practical Application § System Description § § The SDS 1 trip logic consist of 3 channels (D, E, and F). A 2 -out-of-3 voting system for tripping the reactor during the normal operation is used. § The trip logic becomes 1 -out-of-2 during a surveillance test of a channel. Korea Advanced Institute of Science and Technology 18

Practical Application § RGGG modeling § Because trip logic changes from 2 -out-of-3 to 1 -out-of-2 logic, the node of RGGG has to change. § In this case, 2 or more graphs are required to model the system. § This situation can be avoided by making suitable reliability change table. § During the surveillance test of a certain component, let the reliability of appropriate arc be 1, not 0. Korea Advanced Institute of Science and Technology 19

Practical Application < Reliability change table > N 1 D D E F Normal operation N 2 E 2 G Ch. D test Ch. E test N 3 F Ch. F test 1 1 1 § During the surveillance test of channel D, reliability of D becomes 1. So, the RGGG means the 1 -out-of 2 logic whose inputs are E and F. § One RGGG can represent the configuration logic change from 2 -out-of 3 to 1 -out-of-2. Korea Advanced Institute of Science and Technology 20

Summary & Further Study § Two types of dynamic failure mechanisms. § § § Dynamic system whose configuration changes with time can be modeled using RGGG. § § Failure mechanism composed of sequence-dependent events Failure mechanism of which configuration changes with time RGGG is a very intuitive method and has expression power. RGGG can represent a dynamic system by adding reliability change table to original RGGG. It is more intuitive dynamic modeling method than dynamic fault tree or Markov chain method. Further Study § Intuitive method modeling failure mechanism composed of sequencedependent events Korea Advanced Institute of Science and Technology 21

References 1. 2. 3. 4. M. C. Kim, P. H. Seong, “Reliability graph with general gates : an intuitive and practical method for system reliability analysis”, RESS, 2002. S. W. Cho, Jin Jiang, “Comparison of the Unavailability Using FT Model and Markov Model of SDS 1”, NPIC&HMIT, 2006. Marko Cepin, Borut Mavko, “A dynamic fault tree”, RESS, 2002. Todd A. Stephenson, “An Introduction to Bayesian Network Theory and Usage”, IDIAP Research Report, 2000. Korea Advanced Institute of Science and Technology 22