Dynamic rectangular intersection with priorities K Molad Tarjan

Dynamic rectangular intersection with priorities K, Molad, Tarjan

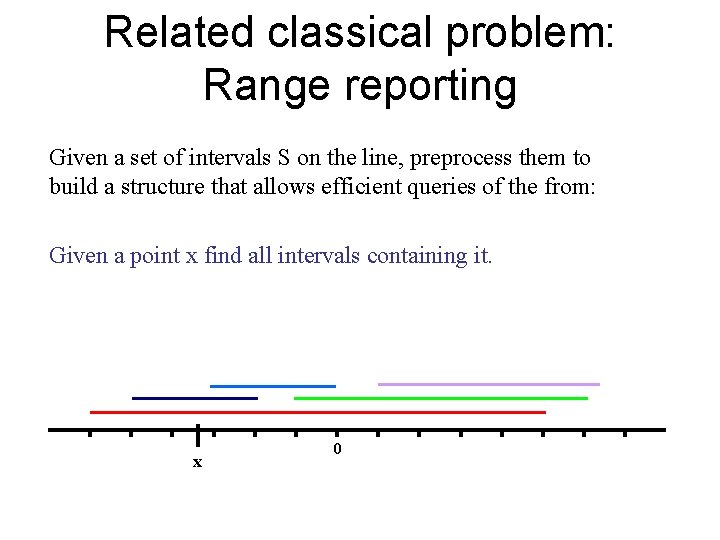
Related classical problem: Range reporting Given a set of intervals S on the line, preprocess them to build a structure that allows efficient queries of the from: Given a point x find all intervals containing it. x 0

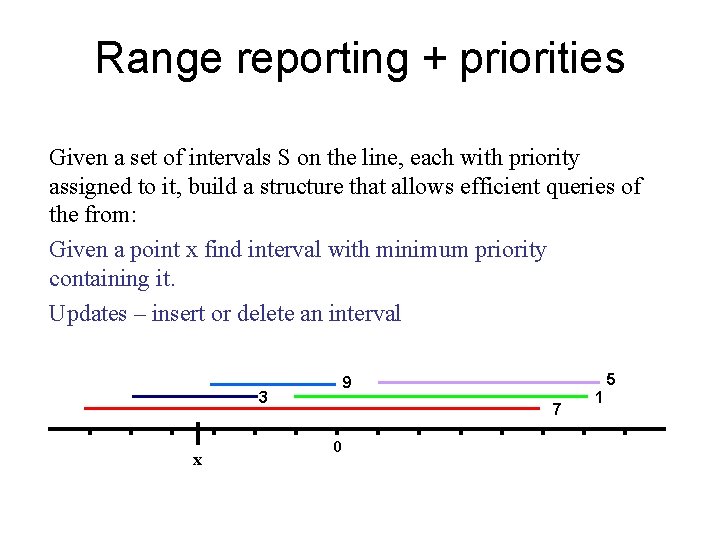
Range reporting + priorities Given a set of intervals S on the line, each with priority assigned to it, build a structure that allows efficient queries of the from: Given a point x find interval with minimum priority containing it. Updates – insert or delete an interval 3 x 5 9 7 0 1

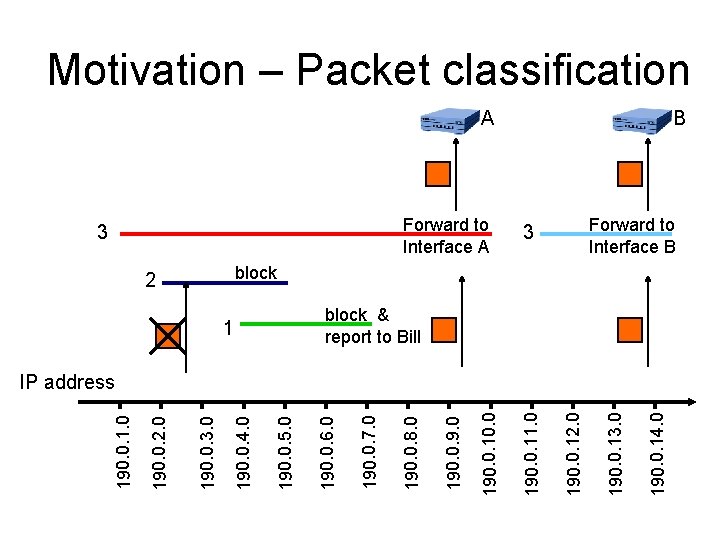
190. 0. 14. 0 3 190. 0. 13. 0 190. 0. 12. 0 Forward to Interface A 190. 0. 11. 0 190. 0. 10. 0 190. 0. 9. 0 3 190. 0. 8. 0 190. 0. 7. 0 1 190. 0. 6. 0 2 190. 0. 5. 0 190. 0. 4. 0 190. 0. 3. 0 190. 0. 2. 0 190. 0. 1. 0 Motivation – Packet classification A B Forward to Interface B block & report to Bill IP address

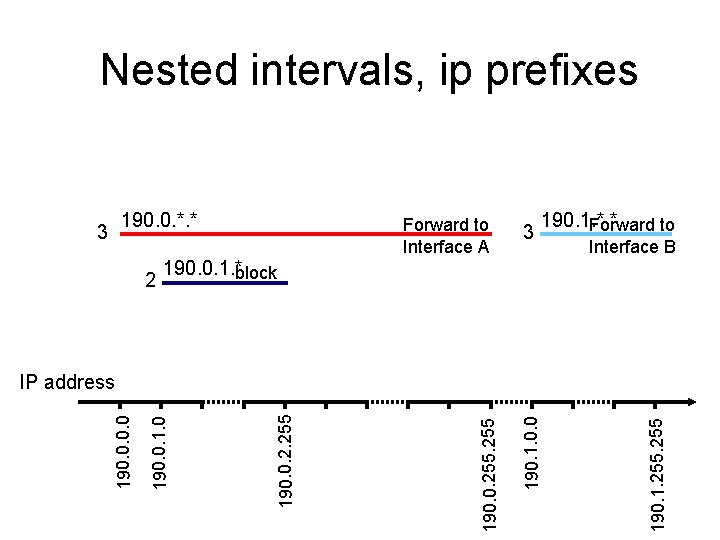
Nested intervals, ip prefixes 190. 0. *. * 3 2 Forward to Interface A 3 190. 1. *. * Forward to Interface B 190. 0. 1. *block 190. 1. 255 190. 1. 0. 0 190. 0. 255 190. 0. 2. 255 190. 0. 1. 0 190. 0 IP address

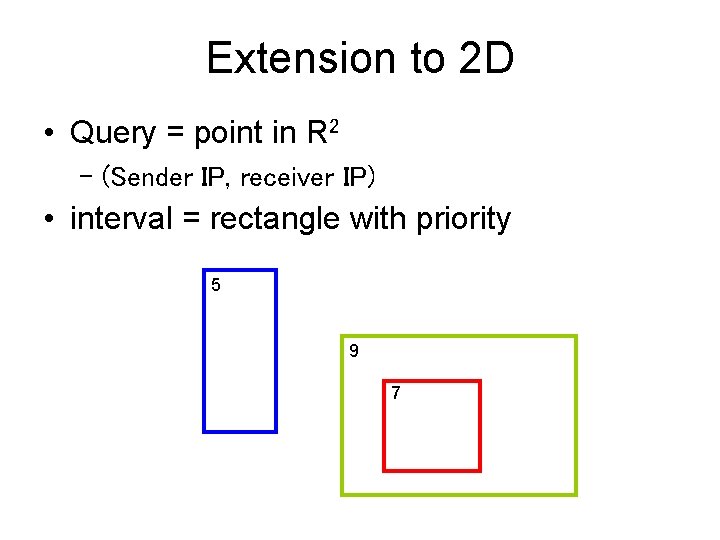
Extension to 2 D • Query = point in R 2 – (Sender IP, receiver IP) • interval = rectangle with priority 5 9 7

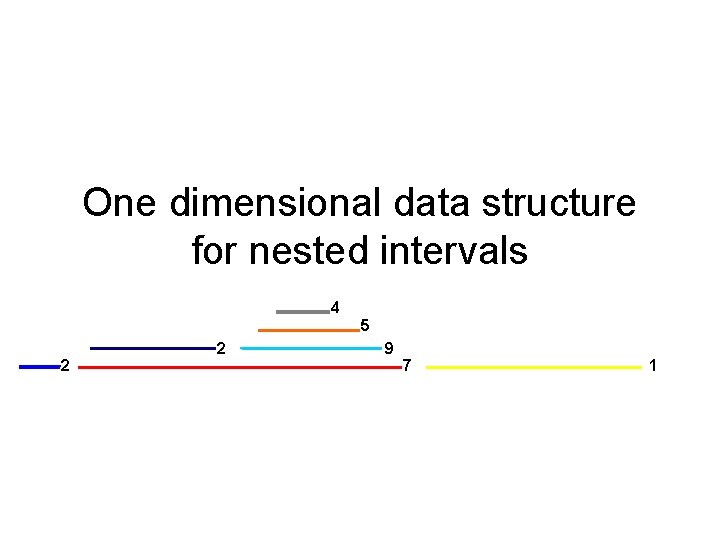
One dimensional data structure for nested intervals 4 5 2 2 9 7 1

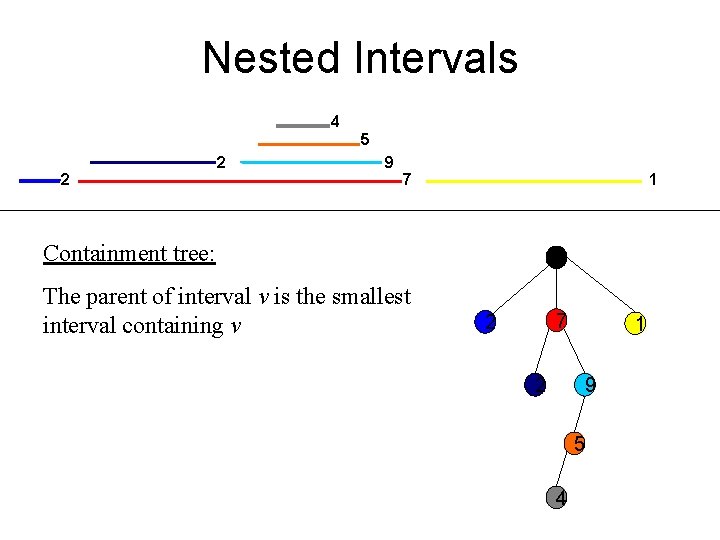
Nested Intervals 4 5 2 2 9 7 1 Containment tree: The parent of interval v is the smallest interval containing v 7 2 2 1 9 5 4

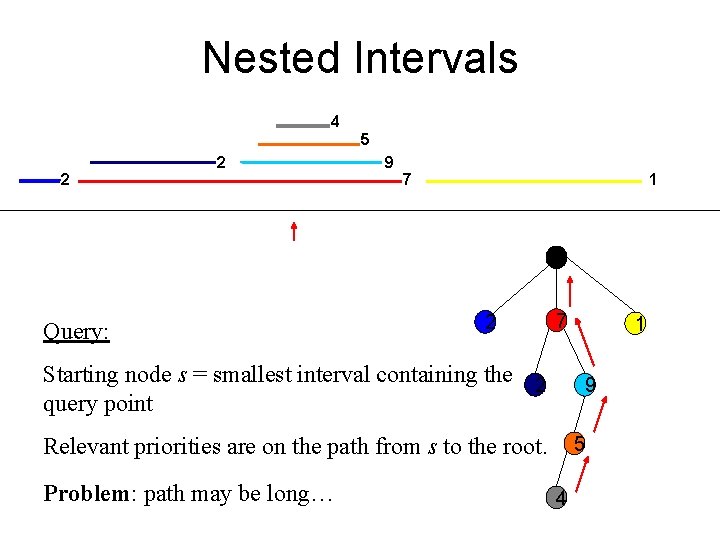
Nested Intervals 4 5 2 2 Query: 9 7 1 2 7 Starting node s = smallest interval containing the 2 query point 9 Relevant priorities are on the path from s to the root. Problem: path may be long… 1 5 4

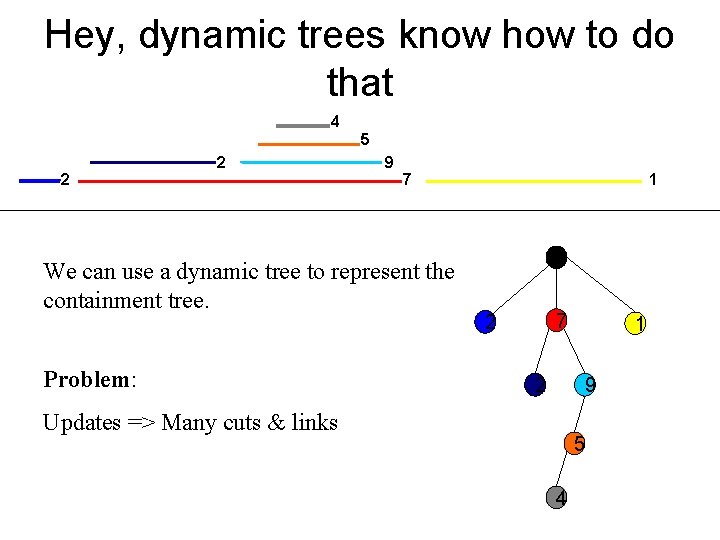
Hey, dynamic trees know how to do that 4 5 2 2 9 7 We can use a dynamic tree to represent the containment tree. Problem: 1 7 2 2 1 9 Updates => Many cuts & links 5 4

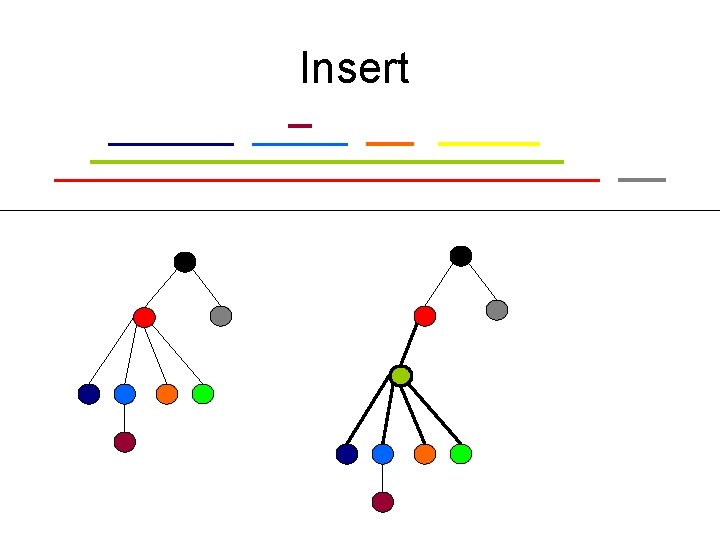
Insert

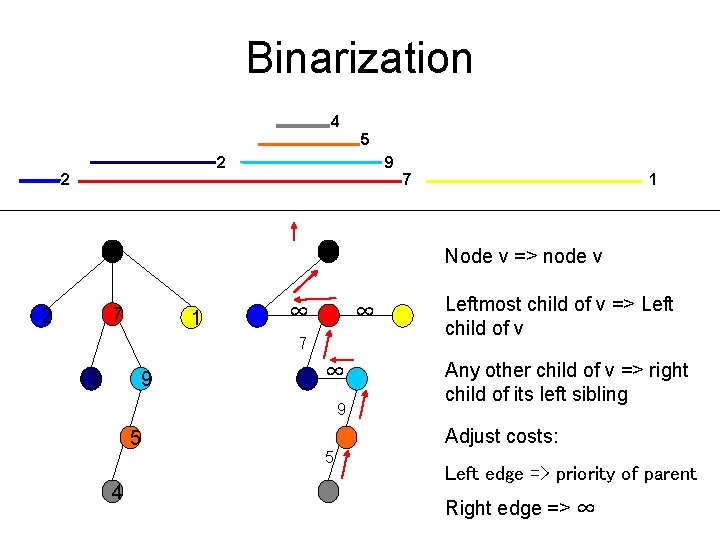
Binarization 4 5 9 2 2 7 1 Node v => node v 7 2 1 ∞ ∞ 7 2 9 ∞ 9 5 4 Leftmost child of v => Left child of v Any other child of v => right child of its left sibling Adjust costs: 5 Left edge => priority of parent Right edge => ∞

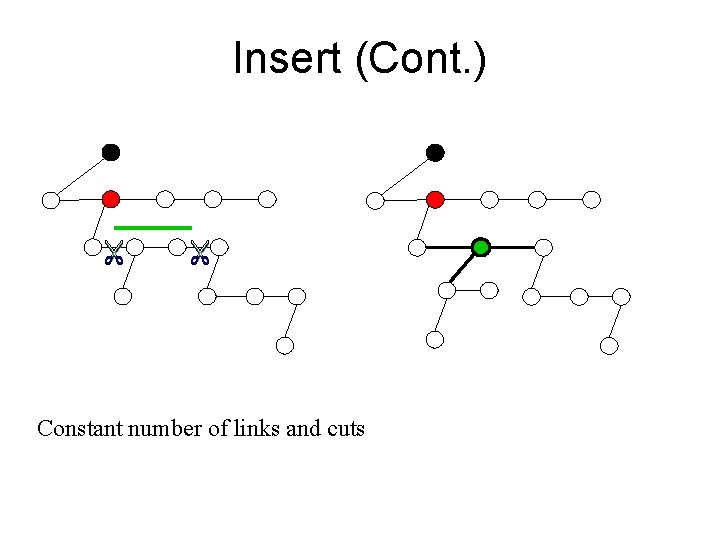
Insert (Cont. ) Constant number of links and cuts

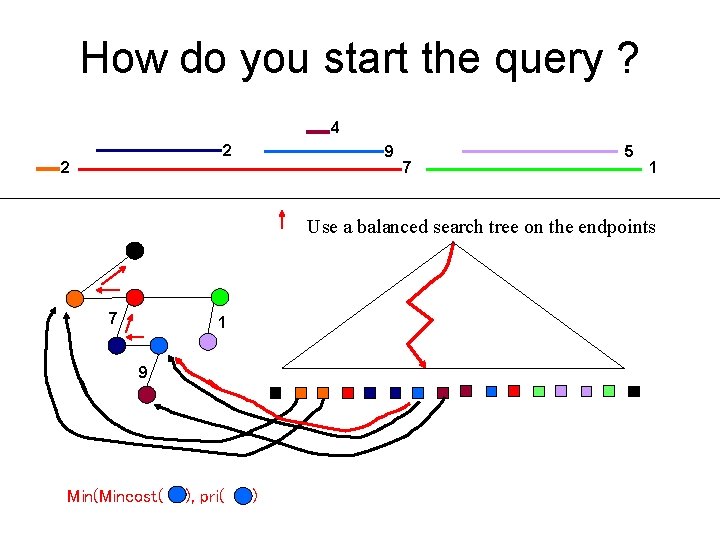
Summary • Containment tree C – Query = min cost on path from starting point to root • Represent C by binarized version B • Represent B by dynamic tree D • How do you find the point to start the query ? • How do you find the edges to cut ?

How do you start the query ? 4 2 2 9 7 5 1 Use a balanced search tree on the endpoints 7 1 9 Min(Mincost( ), pri( ))

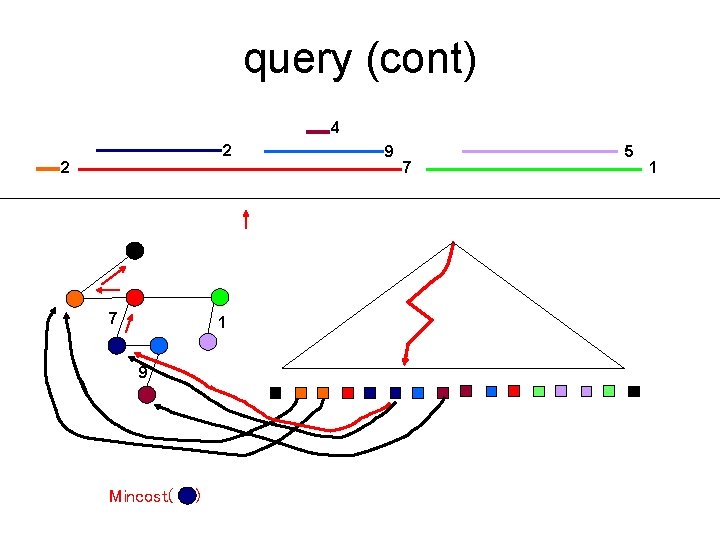
query (cont) 4 2 2 7 1 9 Mincost( ) 9 7 5 1