DYNAMIC PROGRAMMING Matrix Chain Multiplication Optimal Triangulation CSC

DYNAMIC PROGRAMMING: Matrix Chain Multiplication & Optimal Triangulation CSC 252 Algorithms Haniya Aslam

Presentation Overview w Understanding dynamic programming w Dynamic programming vs. Recursion and Demand & Conquer w Matrix chain multiplication w Optimal polygon triangulation w Acknowledgements

Dynamic Programming w w A generalization of iteration and recursion. “Dynamic Programming is recursion’s somewhat neglected cousin. …(It) is the basis of comparison and alignment routines. Bottom-up design: w n n Start at the bottom Solve small sub-problems Store solutions Reuse previous results for solving larger sub-problems

Dynamic Programming cont. Fibonacci: function Fibonacci(n: integer) : integer; var i : index; sum, interm 1, interm 2: integer; begin interm 1: = 0; {F 0} interm 2: = 1; {F 1} for i: =3 to n do sum : =interm 1 + interm 2; interm 1: =interm 2; interm 2: = sum; end {for} Fibonacci : = sum; end {Fibonacci}

Dynamic Programming vs. Recursion and Divide & Conquer w In a recursive program, a problem of size n is solved by first solving a sub-problem of size n-1. w In a divide & conquer program, you solve a problem of size n by first solving a sub-problem of size k and another of size k-1, where 1 < k < n. w In dynamic programming, you solve a problem of size n by first solving all sub-problems of all sizes k, where k < n.

Matrix Chain Multiplication w Given : a chain of matrices {A 1, A 2, …, An}. w Once all pairs of matrices are parenthesized, they can be multiplied by using the standard algorithm as a sub-routine. w A product of matrices is fully parenthesized if it is either a single matrix or the product of two fully parenthesized matrix products, surrounded by parentheses. [Note: since matrix multiplication is associative, all parenthesizations yield the same product. ]

Matrix Chain Multiplication cont. w For example, if the chain of matrices is {A, B, C, D}, the product A, B, C, D can be fully parenthesized in 5 distinct ways: (A ( B ( C D ))), (A (( B C ) D )), ((A B ) ( C D )), ((A ( B C )) D), ((( A B ) C ) D ). w The way the chain is parenthesized can have a dramatic impact on the cost of evaluating the product.

Matrix Chain Multiplication Optimal Parenthesization w Example: A[30][35], B[35][15], C[15][5] minimum of A*B*C A*(B*C) = 30*35*5 + 35*15*5 = 7, 585 (A*B)*C = 30*35*15 + 30*15*5 = 18, 000 w How to optimize: n n Brute force – look at every possible way to parenthesize : Ω(4 n/n 3/2) Dynamic programming – time complexity of Ω(n 3) and space complexity of Θ(n 2).

Matrix Chain Multiplication Structure of Optimal Parenthesization w For n matrices, let Ai. . j be the result of Ai. Ai+1…. Aj w An optimal parenthesization of Ai. Ai+1…An splits the product between Ak and Ak+1 where 1 k < n. w Example, k = 4 (A 1 A 2 A 3 A 4)(A 5 A 6) Total cost of A 1. . 6 = cost of A 1. . 4 plus total cost of multiplying these two matrices together.

Matrix Chain Multiplication Overlapping Sub-Problems w Overlapping sub-problems helps in reducing the running time considerably. n n n Create a table M of minimum Costs Create a table S that records index k for each optimal sub-problem Fill table M in a manner that corresponds to solving the parenthesization problem on matrix chains of increasing length. Compute cost for chains of length 1 (this is 0) Compute costs for chains of length 2 A 1. . 2, A 2. . 3, A 3. . 4, …An-1…n n Compute cost for chain of length n A 1. . n Each level relies on smaller sub-strings

Optimal Polygon Triangulation w A triangulation of a polygon is a set of T chords of the polygon that divide the polygon into disjoint triangles. In a triangulation, no chords intersect (except at end-points) and the set T of chords is maximal: every chord not in T intersects some chord in T. The sides of triangles produced by the triangulation are either chords in the triangulation or sides of the polygon. Every triangulation of an n-vertex convex polygon has n-3 chords and divides the polygon into n-2 triangles. a. b.

Optimal Polygon Triangulation cont. w In the optimal polygon triangulation problem , we are given a polygon P = {v 0, v 1, v 2, …. , vn-1} and a weight function w defined on triangles formed by sides and chords of P. w The problem is to find a triangulation that minimizes the sum of the weights of the triangles in the triangulation. w This problem, like matrix chain multiplication, uses parenthesization. A full parenthesization corresponds to a full binary tree also called a parse tree.

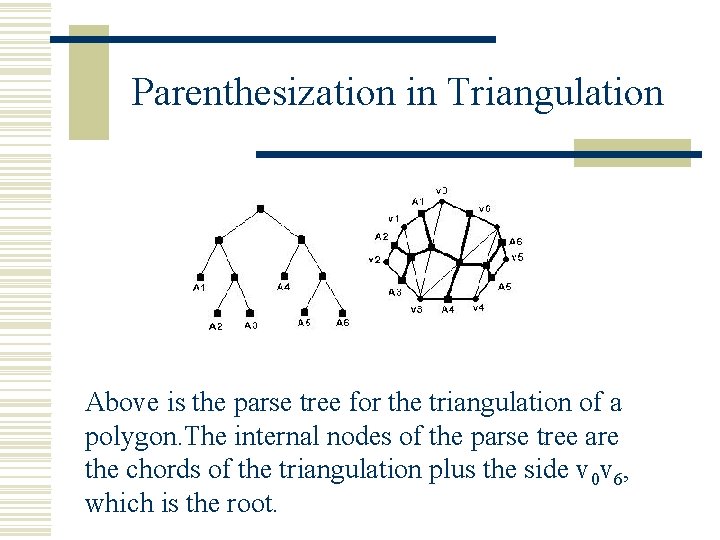
Parenthesization in Triangulation Above is the parse tree for the triangulation of a polygon. The internal nodes of the parse tree are the chords of the triangulation plus the side v 0 v 6, which is the root.

Triangulation and Matrix Chain Multiplication w Since a fully parenthesized product of n matrices corresponds to a parse tree with n leaves, it therefore also corresponds to a triangulation of an (n+1)-vertex polygon. w Each matrix Ai in a product of A 1 A 2…An corresponds to side vi-1 vi of an (n+1)-vertex polygon. w The matrix chain is actually a special case of the optimal triangulation problem.

Triangulation and Matrix Chain Multiplication cont. w Given a matrix chain product A 1 A 2…. AN, we define an (n+1)-vertex convex polygon p = {v 0, v 1, …. , vn}. If matrix Ai has dimensions pi-1 x pi, for I = 1, 2, …, n, the weight function for the triangulation is defined as w(Δvivjvk) = pipjpk w An optimal triangulation of P with respect to this weight function gives the parse tree for an optimal parenthesization of A 1 A 2…. An.

Substructure of an optimal triangulation w Given: an optimal triangulation T of an (n+1)vertex polygon P that includes the triangle Δv 0 vkvn, where 1 k n-1. w The weight of T is the sum of the weights of Δv 0 vkvn and triangles in the triangulation of the two sub-polygons {v 0, v 1, …. vk} and {vk, vk+1, …. vn}. w The triangulation of the sub-polygons determined by T , therefore, must be optimal, since a lesserweight triangulation of either sub-polygon would contradict the minimality of the eight of T.

A Recursive Solution w Given, for 1 I j n: l T[i, j] is the weight of an optimal triangulation of the polygon {vi-1, vi, …. . vj} [Since m[i, j] is the minimum cost of computing the matrix chain sub-product Ai. Ai+1…. Aj] w In the case of a 2 -vertex polygon: t[i, i] = 0 for i = 1, 2, …, n. w To minimize over all vertices vk, where k = i, i+1, …j-1, the weight of Δvi 1 vkvj plus the weights of the optimal triangulation of the polygons {vi-1, vi, …. , vk} and {vk, vk+1, …, vj}. w The recursive solution then is: If i < j, T[i, j] = min {t[i, k] + t[k+1, j] + w(Δvi-1 vkvj)} i k j-1

Acknowledgments w w w w http: //www-cse/uta/edu/~holder/courses/cse 5311/lectures/18/node 18. html http: //www. middlebury. edu/~dickerso/ccsc/ugcg. html http: //www. eecs. harvard. edu/~nr/cs 152/readings/dynamic. html http: //www. catalase. com/dprog. htm http: //mail. informs. org/classes/dynamic/node 1. html http: //cse. hanyang. ac. kr/~jmchoi/c… 6 -2/algorithm/classnote/node 6. html http: //people. bu. edu/rlynch/cs 566/sld 002. htm