Dynamic Programming for Pairwise Alignment 2 Dr Alexei

Dynamic Programming for Pairwise Alignment 2 Dr Alexei Drummond Department of Computer Science alexei@cs. auckland. ac. nz Semester 2, 2006

Dynamic Programming for Pairwise Alignment Review Dynamic programming algorithm for global alignment (Needleman & Wunsch) Given sequences: F(i, j) = score of best alignment between and 2

Dynamic Programming for Pairwise Alignment Principle of Optimality Optimal alignment 3

Dynamic Programming for Pairwise Alignment Principle of Optimality Optimal alignment Looks like …… 4

Dynamic Programming for Pairwise Alignment Principle of Optimality Optimal alignment Looks like …… or …………… 5

Dynamic Programming for Pairwise Alignment Principle of Optimality Optimal alignment Looks like …… or …………… 6

Dynamic Programming for Pairwise Alignment Principle of Optimality Optimal alignment Looks like …… or …………… so …………… 7

Dynamic Programming for Pairwise Alignment Basis 8

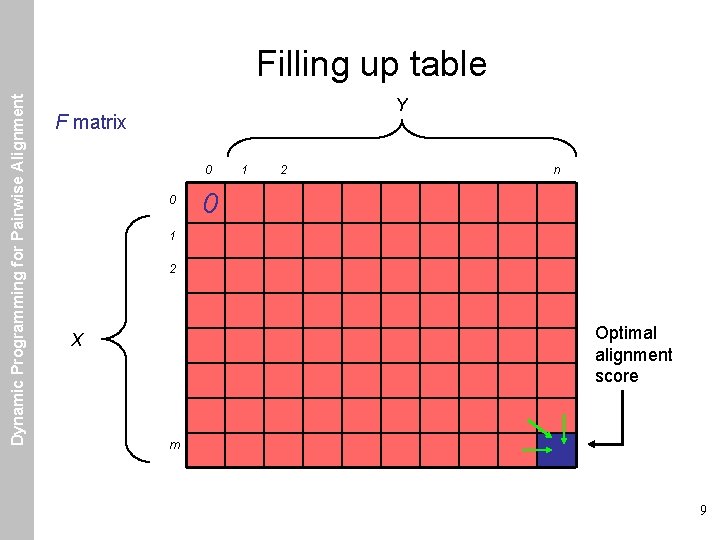
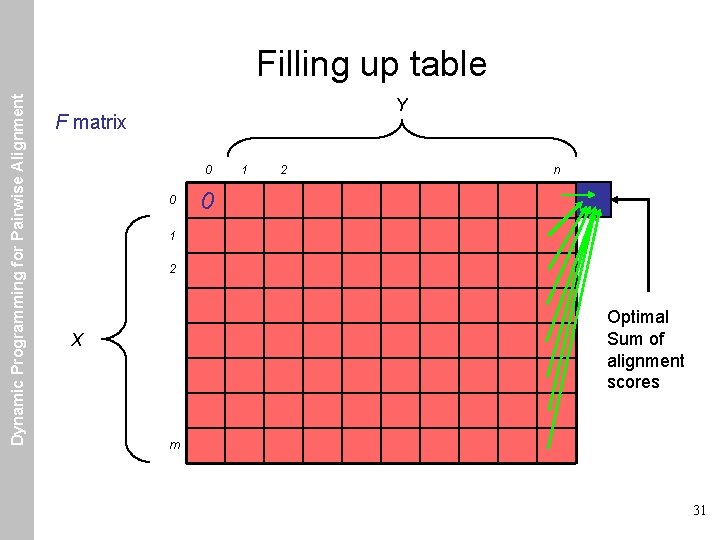
Dynamic Programming for Pairwise Alignment Filling up table Y F matrix 0 0 1 2 n 0 1 2 Optimal alignment score X m 9

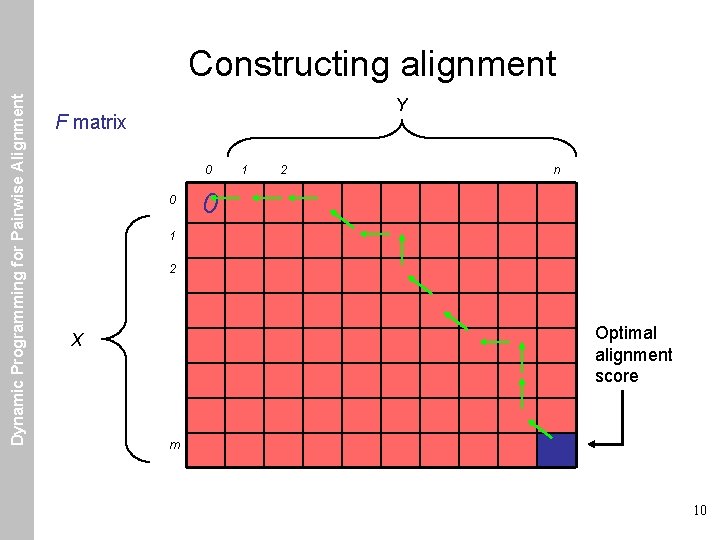
Dynamic Programming for Pairwise Alignment Constructing alignment Y F matrix 0 0 1 2 n 0 1 2 Optimal alignment score X m 10

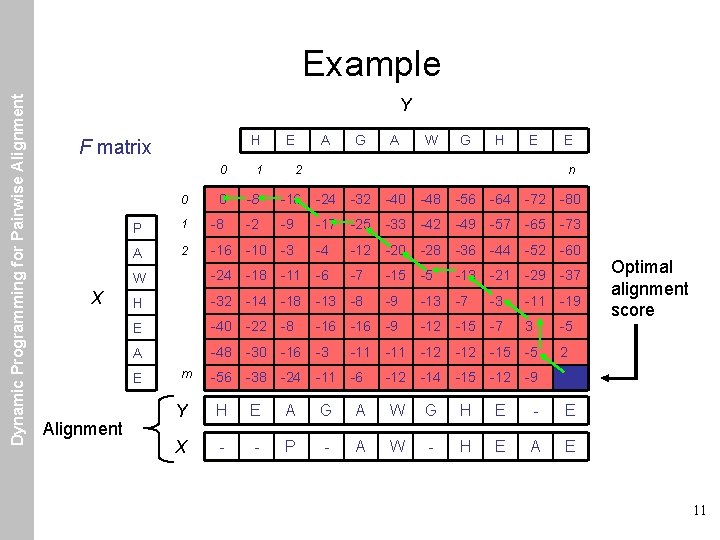
Dynamic Programming for Pairwise Alignment Example Y H F matrix 0 X 1 A G A W G H E E 2 n 0 0 -8 -16 -24 -32 -40 -48 -56 -64 -72 -80 P 1 -8 -2 -9 -17 -25 -33 -42 -49 -57 -65 -73 A 2 -16 -10 -3 -4 -12 -20 -28 -36 -44 -52 -60 W -24 -18 -11 -6 -7 -15 -5 -13 -21 -29 -37 H -32 -14 -18 -13 -8 -9 -13 -7 -3 -11 -19 E -40 -22 -8 -16 -9 -12 -15 -7 3 -5 A -48 -30 -16 -3 -11 -12 -15 -5 2 -56 -38 -24 -11 -6 -12 -14 -15 -12 -9 1 Y H E A G A W G H E - E X - - P - A W - H E A E E Alignment E m Optimal alignment score 11

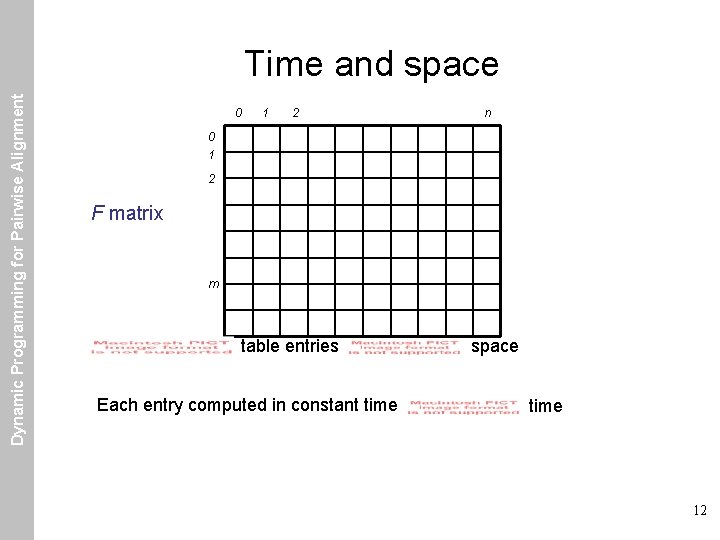
Dynamic Programming for Pairwise Alignment Time and space 0 1 2 n 0 1 2 F matrix m table entries Each entry computed in constant time space time 12

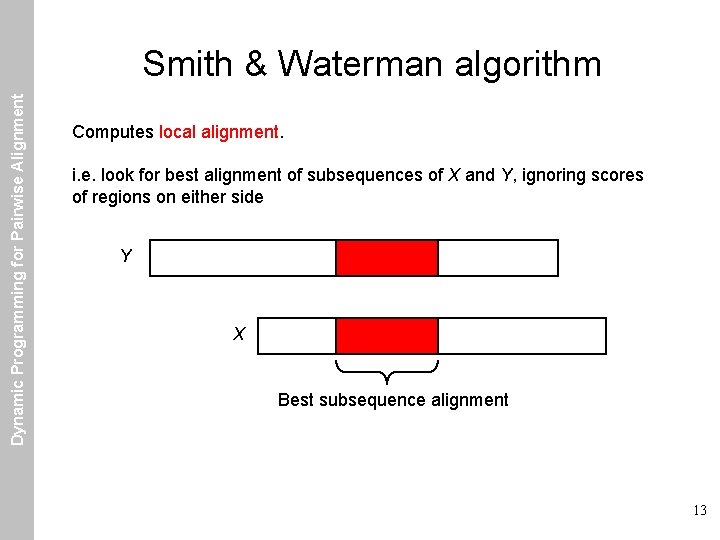
Dynamic Programming for Pairwise Alignment Smith & Waterman algorithm Computes local alignment. i. e. look for best alignment of subsequences of X and Y, ignoring scores of regions on either side Y X Best subsequence alignment 13

Dynamic Programming for Pairwise Alignment Recurrences Basis: 14

Dynamic Programming for Pairwise Alignment Example 15

Dynamic Programming for Pairwise Alignment Example Alignment Y A W G H E X A W H E 16

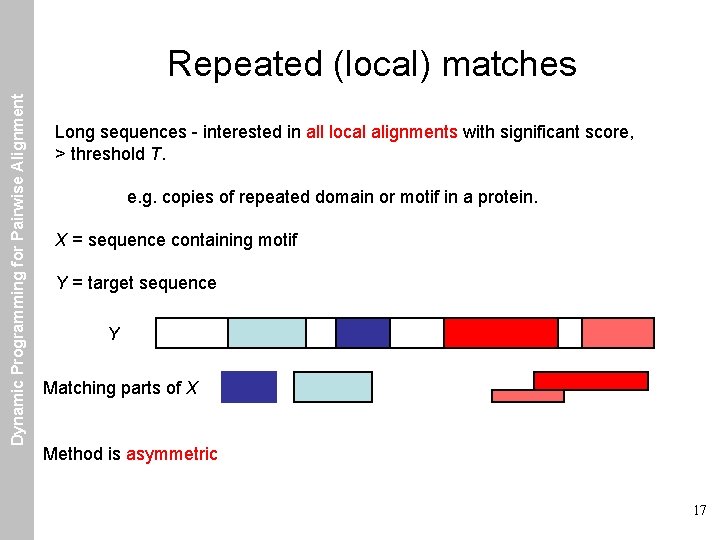
Dynamic Programming for Pairwise Alignment Repeated (local) matches Long sequences - interested in all local alignments with significant score, > threshold T. e. g. copies of repeated domain or motif in a protein. X = sequence containing motif Y = target sequence Y Matching parts of X Method is asymmetric 17

Dynamic Programming for Pairwise Alignment Principle of Optimality Given sequences Define F(i, j) (i ≥ 1) = best sum of match scores in and assuming is in a matched region and match ends in or 18

Dynamic Programming for Pairwise Alignment Ends of matches best sum of completed match scores to assuming that is not in a matched region Row 0 therefore marks unmatched regions and ends of matches in Y. 19

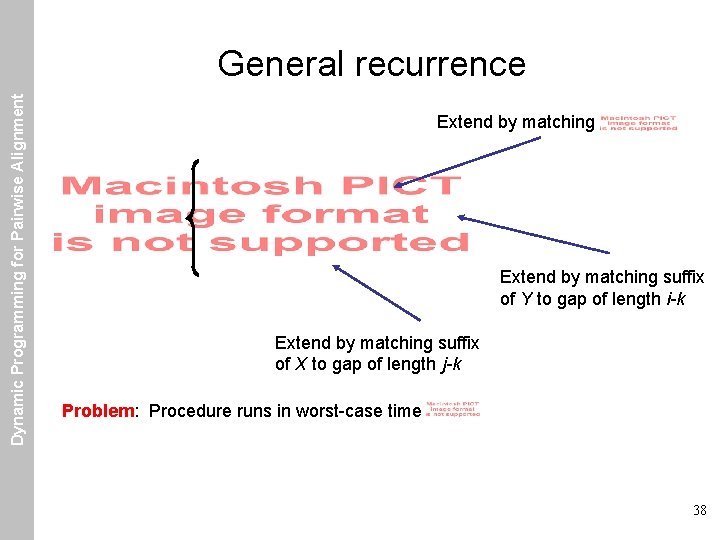
Dynamic Programming for Pairwise Alignment General recurrence Start of new match Extension of previous match 20

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 21

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 22

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 23

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 24

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 25

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 26

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 27

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 28

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 29

Dynamic Programming for Pairwise Alignment Filling up table F matrix Y 0 0 1 2 n 0 1 2 X m 30

Dynamic Programming for Pairwise Alignment Filling up table Y F matrix 0 0 1 2 n 0 1 2 Optimal Sum of alignment scores X m 31

Dynamic Programming for Pairwise Alignment Example Extra cell for final total score 32

Dynamic Programming for Pairwise Alignment Example Extra cell for final total score Alignment Y H E A G A W G H E E X H E A . A W - H E . 33

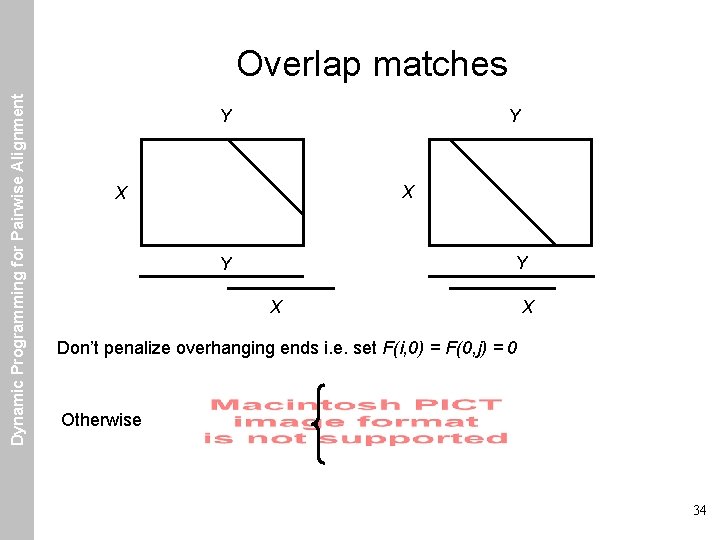
Dynamic Programming for Pairwise Alignment Overlap matches Y Y X X Don’t penalize overhanging ends i. e. set F(i, 0) = F(0, j) = 0 Otherwise 34

Dynamic Programming for Pairwise Alignment Example 35

Dynamic Programming for Pairwise Alignment Example Alignment Y G A W G H E E X P A W H E A 36

Dynamic Programming for Pairwise Alignment Affine gap penalities g(g) = -d - (g-1)e • Affine score: gap-open penality gap-extension penalty • Different penalties associated with extending alignment with gap symbol Y=CCTWP X=CSTW- different from Y=CCTWP X=CST-- 37

Dynamic Programming for Pairwise Alignment General recurrence Extend by matching suffix of Y to gap of length i-k Extend by matching suffix of X to gap of length j-k Problem: Procedure runs in worst-case time 38

Dynamic Programming for Pairwise Alignment version Extra variables 39

Dynamic Programming for Pairwise Alignment Recurrences aligned to start of gap aligned to continuation of gap Procedure runs in worstcase time 40

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 41

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 42

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 43

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 44

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 45

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 46

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 47

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 48

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 49

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 50

Dynamic Programming for Pairwise Alignment Linear space alignment Y F matrix 0 1 2 n 0 1 2 X m 51

Dynamic Programming for Pairwise Alignment Linear space algorithm From top + From bottom = k such that is maximized k is on path of optimal alignment 52

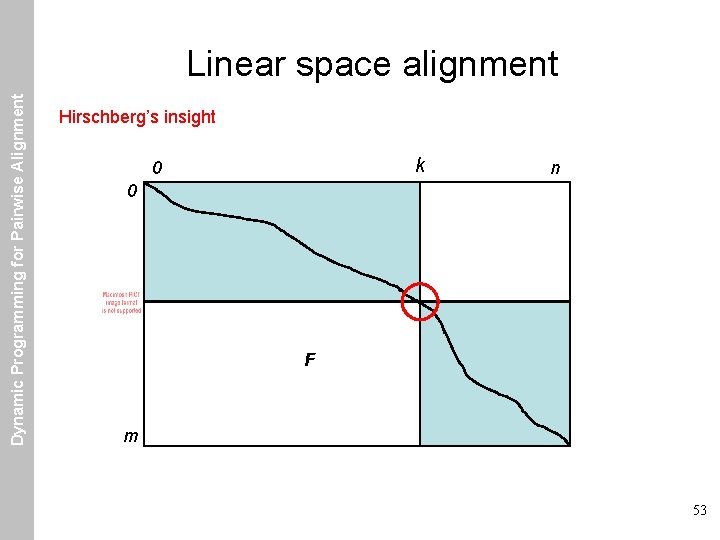
Dynamic Programming for Pairwise Alignment Linear space alignment Hirschberg’s insight k 0 n 0 F m 53

Dynamic Programming for Pairwise Alignment Linear space alignment Hirschberg’s insight k 0 n 0 F m 54

Dynamic Programming for Pairwise Alignment Software for pairwise alignment Pure D. P. runs in time Example 100 million residues in database Search sequence of length 10, 000 # F matrix cells to be calculated: Computer speed: 10 million cells a second Total time: 100, 000 seconds = 28 hours (approx. ) 55

Dynamic Programming for Pairwise Alignment Heuristic methods FASTA (Pearson & Lipman, 1988) Position in X Position in Y Words in X and Y (length ktup) cgtta . . . • • …, ( i, j ), … . . . sort matches on j - i extend best matches (ungapped) join neighbouring matches by inserting gaps realign best matches by dynamic programming 56

Dynamic Programming for Pairwise Alignment Sensitivity Tradeoff High values of ktup: faster search, but may miss significant matches Low values of ktup: catches more matches, but slower ktup = 1 for sensitivity close to dynamic programming Available from http: //www. fasta. bioch. virginia. edu/ 57

Dynamic Programming for Pairwise Alignment Example Input sequences Output matches 58

Dynamic Programming for Pairwise Alignment Example More matches 59

Dynamic Programming for Pairwise Alignment BLAST Developed by Altschul & al (1990) Preprocesses query sequence Makes list of “neighbourhood words” with match > T Tries to extend “seed” matches (ungapped) in database sequences GAPPED-BLAST looks for gapped alignments 60

Dynamic Programming for Pairwise Alignment Genetics Computer Group package GCG at University of Wisconsin Commercial package (http: //www. gcg. com/) 61

Dynamic Programming for Pairwise Alignment GAP (“Global Alignment Program” ? ) Needleman & Wunsch algorithm Input in GCG format Use GETSEQ !!NA_SEQUENCE 1. 0 GETSEQ from gcg, August 14, 19103 12: 19. Length: 389 August 14, 19103 12: 19 Type: N Check: 9580 1 AAATGATAAA CTATTTTACT TTATGTCTAA GGTCTTTCAT AATATGAAAT 51 AGAATGTAGA TATTGCAACA ATAGCATTTT TGGAGACAGC TACCTCCTTT 101 ACCAGGAATA ATCTTTGCAT GTCACATTTA GAGATAAAGC TCAAAATGCA 151 AATCCTTCCC CTGAGAGTGG GAAAGCATTA ACAAATGAGA GTGGGAAAAG 201 CATTAACAAA GCATTAACAC AGGTCTTTAC ATATTCAAAA TATTAAACTA 251 ATGCTAGGAT TATAGACTTG ATTTTAAGAC ATGGTAGTTA ATAGAAAAGT 301 TCTAGATTGA AAACAATTTT GCAAAAATAT ACATTTGGTA TATGTGTATA 351 TATGTG GTATAT ATCNACTAGG GAAAATATA . . 62

Dynamic Programming for Pairwise Alignment Example 63

Dynamic Programming for Pairwise Alignment Display file 64

Dynamic Programming for Pairwise Alignment Bestfit Smith & Waterman algorithm Local alignment Same interface as GAP 65

Dynamic Programming for Pairwise Alignment Bestfit display file 66

Dynamic Programming for Pairwise Alignment Wordsearch Algorithm similar to algorithm of Wilbur and Lipman (1983). Compares one sequence (the query) to any group of sequences. Comparisons can be viewed as set of dot-plots. Search finds registers of comparison (diagonals) that have the largest number of short perfect matches (words). Best segment of similarity along each diagonal viewed with program SEGMENTS. 67

Dynamic Programming for Pairwise Alignment Wordsearch example 68

Dynamic Programming for Pairwise Alignment Short 1. word contents 69

Dynamic Programming for Pairwise Alignment Run SEGMENTS 70

Dynamic Programming for Pairwise Alignment Short 1. pairs contents 71

Dynamic Programming for Pairwise Alignment Short 1. pairs (continued) 72

Dynamic Programming for Pairwise Alignment EMBOSS 73

Dynamic Programming for Pairwise Alignment Suite of programs 74