Dynamic Programming Fibonacci sequence 0 1 1 2

Dynamic Programming Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, …

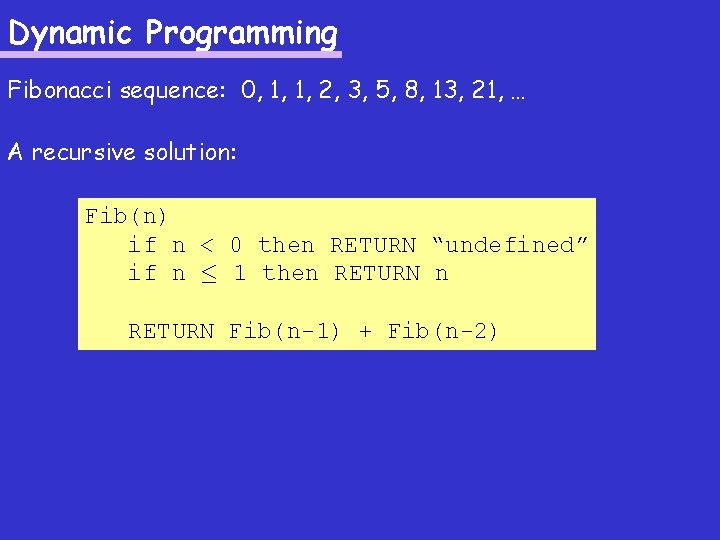
Dynamic Programming Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, … A recursive solution: Fib(n) if n < 0 then RETURN “undefined” if n · 1 then RETURN Fib(n-1) + Fib(n-2)

Dynamic Programming Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, … A recursive solution: Fib(n) if n < 0 then RETURN “undefined” if n · 1 then RETURN Fib(n-1) + Fib(n-2) Can do better (faster) ?

Dynamic Programming Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, … A recursive solution: Fib(n) if n < 0 then RETURN “undefined” if n · 1 then RETURN Fib(n-1) + Fib(n-2) Can do better (faster) ? YES ! Just store Fib[k] in an array !

Dynamic Programming Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, … A recursive solution: Fib(n) Fib[0] = 0; Fib[1] = 1; for i=2 to n do Fib[i] = Fib[i-1] + Fib[i-2]; RETURN Fib[n]; Can do better (faster) ? YES ! Just store Fib[k] in an array !

KNAPSACK – divisible Input: a number W and a set of n items, the i-th item has a weight wi and a cost ci Output: a subset of items with total weight · W Objective: maximize cost Version 1: Items are divisible.

KNAPSACK – divisible Input: a number W and a set of n items, the i-th item has a weight wi and a cost ci Output: a subset of items with total weight · W Objective: maximize cost Version 1: Items are divisible. GREEDY!

KNAPSACK – divisible: a greedy solution KNAPSACK-DIVISIBLE(n, c, w, W) sort items in decreasing order of ci/wi; i = 1; current. W = 0; while (current. W + wi < W) { take item of weight wi and cost ci; current. W += wi; i++; } take W-current. W portion of item i

KNAPSACK – indivisible Assumption 2: Items are indivisible. Does previous algorithm work for this version of KNAPSACK?

KNAPSACK – indivisible: a dyn-prog solution The heart of the algorithm:

KNAPSACK – indivisible: a dyn-prog solution The heart of the algorithm: S[k][v] =

KNAPSACK – indivisible: a dyn-prog solution The heart of the algorithm: S[k][v] = maximum cost of a subset of the first k items, where the weight of the subset equals v

KNAPSACK – indivisible: a dyn-prog solution The heart of the algorithm: S[k][v] = maximum cost of a subset of the first k items, where the weight of the subset equals v KNAPSACK-INDIVISIBLE(n, c, w, W) 1. init S[k][v] to -1 for every k=1, …, n and every v=0, …, W 2. init S[k][0]=0 for every k=1, …, n 3. for v=1 to W do 4. for k=1 to n do 5. S[k][v] = S[k-1][v] 6. if (wk · v) and (S[k-1][v-wk]+ck > S[k][v]) then 7. S[k][v] = S[k-1][v-wk]+ck 8. RETURN maxv S[N][v]

KNAPSACK – indivisible: a dyn-prog solution The heart of the algorithm: Running time: S[k][v] = maximum cost of a subset of the first k items, where the weight of the subset equals v KNAPSACK-INDIVISIBLE(n, c, w, W) 1. init S[k][v] to -1 for every k=1, …, n and every v=0, …, W 2. init S[k][0]=0 for every k=1, …, n 3. for v=1 to W do 4. for k=1 to n do 5. S[k][v] = S[k-1][v] 6. if (wk · v) and (S[k-1][v-wk]+ck > S[k][v]) then 7. S[k][v] = S[k-1][v-wk]+ck 8. RETURN maxv S[N][v]

KNAPSACK – indivisible: a dyn-prog solution The heart of the algorithm: How to output a solution? S[k][v] = maximum cost of a subset of the first k items, where the weight of the subset equals v KNAPSACK-INDIVISIBLE(n, c, w, W) 1. init S[k][v] to -1 for every k=1, …, n and every v=0, …, W 2. init S[k][0]=0 for every k=1, …, n 3. for v=1 to W do 4. for k=1 to n do 5. S[k][v] = S[k-1][v] 6. if (wk · v) and (S[k-1][v-wk]+ck > S[k][v]) then 7. S[k][v] = S[k-1][v-wk]+ck 8. RETURN maxv S[N][v]

Longest Common Subsequence Input: two strings, u and v Output: a common substring Objective: maximize length of the substring Example: carrot party

Longest Common Subsequence Input: two strings, u and v Output: a common substring Objective: maximize length of the substring The heart of the solution:

Longest Common Subsequence Input: two strings, u and v Output: a common substring Objective: maximize length of the substring The heart of the solution: S[j][k] =

Longest Common Subsequence Input: two strings, u and v Output: a common substring Objective: maximize length of the substring The heart of the solution: S[j][k] = the length of the longest common substring of strings u[1…j] and v[1…k]

Longest Common Subsequence S[j][k] = the length of the longest common substring of strings u[1…j] and v[1…k] LONGEST-COMMON-SUBSEQUENCE(u, v) 1. init S[j][k] to 0 for every j=0, …, |u| and every k=0, …, |v| 2. for j=1 to |u| do 3. for k=1 to |v| do 4. S[j][k] = max{ S[j-1][k], S[j][k-1] } 5. if (u[j] = v[k]) then 6. S[j][k] = S[j-1][k-1]+1 7. RETURN S[|u|][|v|]