Dynamic Programming Fibonacci numbers 0 1 1 2

Dynamic Programming

Fibonacci numbers • 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . • Each number is the sum of the preceding two. • Recursive definition: – F(0) = 0; – F(1) = 1; – F(n) = F(n-1)+ F(n-2);

Recursive Fibonacci

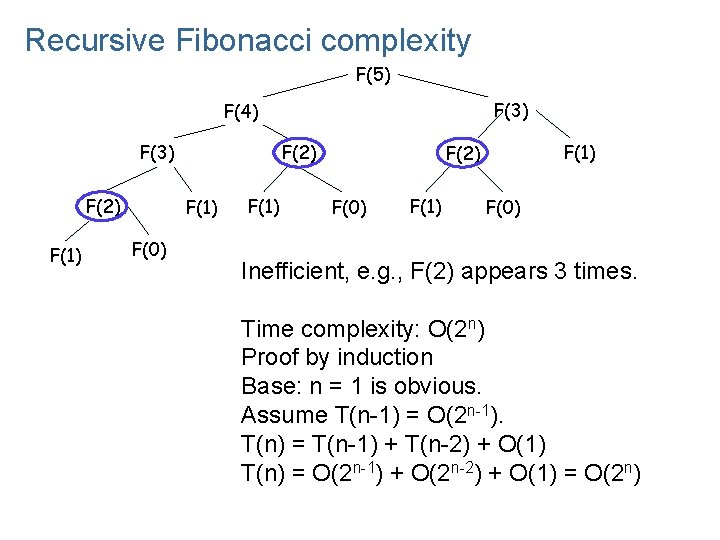
Recursive Fibonacci complexity F(5) F(3) F(4) F(3) F(2) F(1) F(0) F(1) F(2) F(0) F(1) F(0) Inefficient, e. g. , F(2) appears 3 times. Time complexity: O(2 n) Proof by induction Base: n = 1 is obvious. Assume T(n-1) = O(2 n-1). T(n) = T(n-1) + T(n-2) + O(1) T(n) = O(2 n-1) + O(2 n-2) + O(1) = O(2 n)

Dynamic Fibonacci Space complexity: O(n) Time complexity: O(n) Improve space to O(1)? • Set up a recurrence to relate a bigger solution to smaller solutions. • Solve smaller instances once. • Record solutions in a table. • Extract bigger solutions from these records.

Edit Distance: Example TGCATAT ATCCGAT in 5 steps TGCATAT TGCATA TGCAT ATCCAT ATCCGAT (delete last T) (delete last A) (insert A at front) (change G to C) (insert G before last A) (Done) Can it be done in less number of steps?

Class Ex. What is the distance between “informatik” and “information”? Given: two strings A = a 1 a 2. . am and B = b 1 b 2. . . bn Edit operations: 1. Replace one character in A by a character from B 2. Delete one character from A 3. Insert one character from B Wanted: minimal cost D(A, B) for a sequence of edit operations to transform A into B. How to transform “informatik” into “information” using the least number of edit operations?

Similarity of strings What is the distance between “informatik” and “interpolation”? i i n n f t - e r - o r p o l m - a a t t i i k o n Given: two strings A = a 1 a 2. . am and B = b 1 b 2. . . bn Edit operations: 1. Replace one character in A by a character from B 2. Delete one character from A 3. Insert one character from B Wanted: minimal cost D(A, B) for a sequence of edit operations to transform A into B.

Cost model:

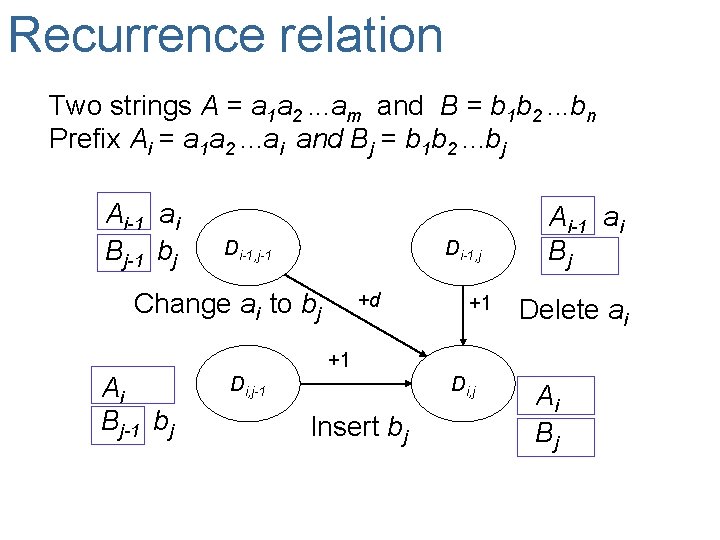
Recurrence relation Two strings A = a 1 a 2. . . am and B = b 1 b 2. . . bn Prefix Ai = a 1 a 2. . . ai and Bj = b 1 b 2. . . bj Ai-1 ai Bj-1 bj Di-1, j-1 Di-1, j Change ai to bj +d +1 Ai-1 ai Bj Delete ai +1 Ai Bj-1 bj Di, j-1 Di, j Insert bj Ai Bj

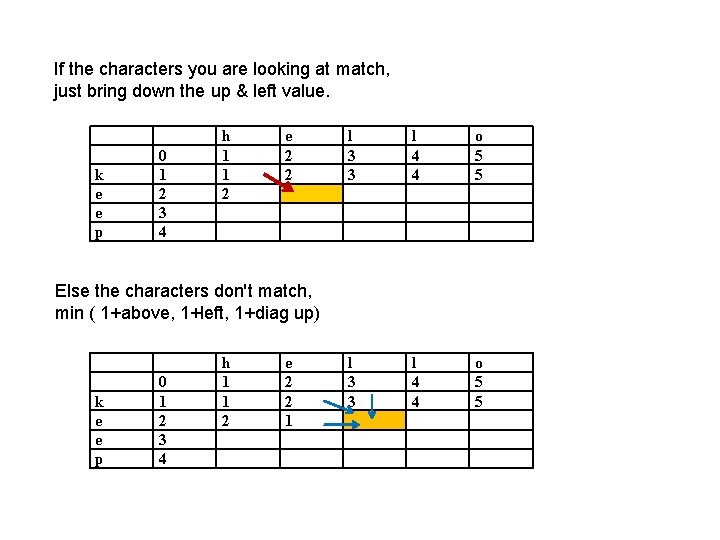
If the characters you are looking at match, just bring down the up & left value. k e e p 0 1 2 3 4 h 1 1 2 e 2 2 l 3 3 l 4 4 o 5 5 Else the characters don't match, min ( 1+above, 1+left, 1+diag up) k e e p 0 1 2 3 4 h 1 1 2 e 2 2 1

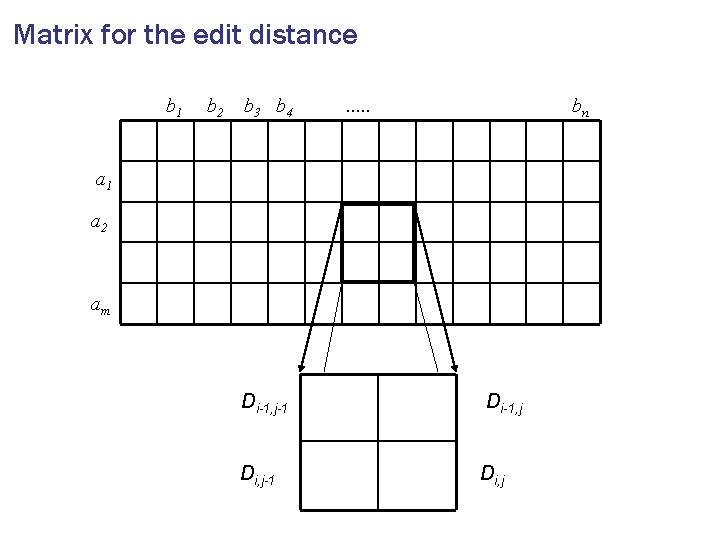
Matrix for the edit distance b 1 b 2 b 3 b 4 . . . bn a 1 a 2 am Di-1, j-1 Di-1, j Di, j-1 Di, j

Algorithm for the edit distance Algorithm edit_distance Input: two strings A = a 1. . am and B = b 1. . . bn Output: the matrix D = (Dij) O(n 2) time. It can be improved to use 1 D[0, 0] : = 0 linear space 2 for i : = 1 to m do D[i, 0] = i 3 for j : = 1 to n do D[0, j] = j 4 for i : = 1 to m do 5 for j : = 1 to n do 6 D[i, j] : = min( D[i - 1, j] + 1, 7 D[i, j - 1] + 1, 8 D[i – 1, j – 1] + c(ai, bj))

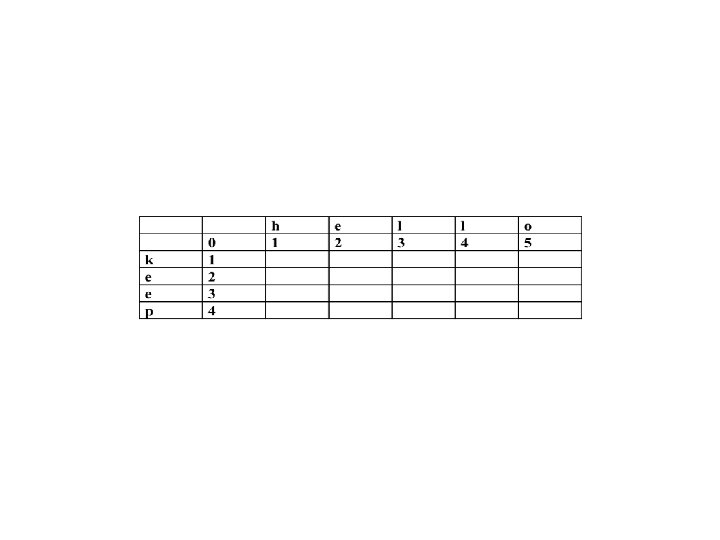
Algorithm edit_distance Input: two strings A = a 1. . am and B = b 1. . . bn Output: the matrix D = (Dij) 1 D[0, 0] : = 0 Class Ex. 2 for i : = 1 to m do D[i, 0] = i Distance between 3 for j : = 1 to n do D[0, j] = j “hello” and “keep” 4 for i : = 1 to m do 5 for j : = 1 to n do 6 D[i, j] : = min( D[i - 1, j] + 1, 7 D[i, j - 1] + 1, 8 D[i – 1, j – 1] + c(ai, bj))

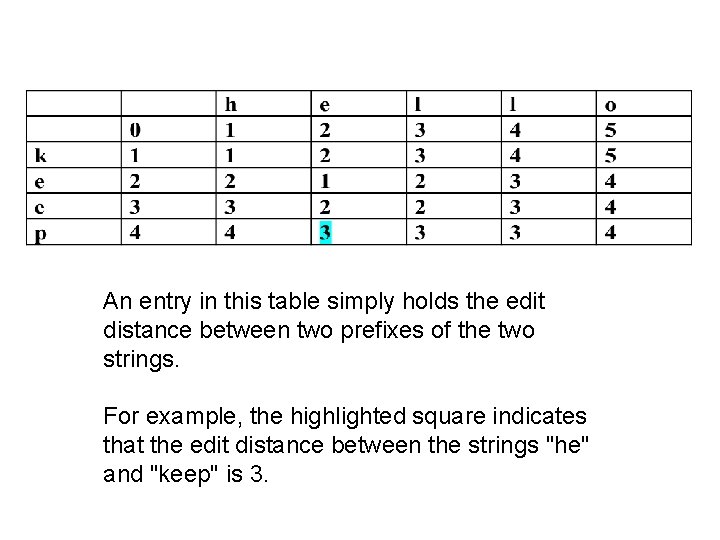
An entry in this table simply holds the edit distance between two prefixes of the two strings. For example, the highlighted square indicates that the edit distance between the strings "he" and "keep" is 3.

Summary 1. Dynamic programming is a technique for solving problems with overlapping subproblems. 2. These subproblems arise from a recurrence relating a solution to a given problem with solutions to its smaller subproblems of the same type. 3. Dynamic programming suggests solving each smaller subproblem once and recording the results in a table from which a solution to the original problem can be then obtained. 4. Principle of optimality: an optimal solution to any optimization problem is composed of optimal solutions to its subproblems.