Dynamic Programming Expected Outcomes n Students should be

Dynamic Programming

Expected Outcomes n Students should be able to n n Write down the four steps of dynamic programming Compute a Fibonacci number and the binomial coefficients by dynamic programming Compute the longest common subsequence and the shortest common supersequence of two given sequences by dynamic programming Solve the invest problem by dynamic programming

Dynamic Programming n n Dynamic Programming is a general algorithm design technique. Invented by American mathematician Richard Bellman in the 1950 s to solve optimization problems Main idea: n solve several smaller (overlapping) subproblems n record solutions in a table so that each subproblem is only solved once n final state of the table will be (or contain) solution Dynamic programming vs. divide-and-conquer n partition a problem into overlapping subproblems and independent ones n store and not store solutions to subproblems

Frame of Dynamic Programming n Problem solved n n Solution can be expressed in a recursive way Sub-problems occur repeatedly Subsequence of optimal solution is an optimal solution to the sub-problem Frame n n Characterize the structure of an optimal solution Recursively define the value of an optimal solution Compute the value of an optimal solution in a bottom-up fashion Construct an optimal solution from computed information

Three basic components n The development of a dynamic programming algorithm has three basic components: n n n A recurrence relation (for defining the value/cost of an optimal solution); A tabular computation (for computing the value of an optimal solution); A backtracing procedure (for delivering an optimal solution).

Example: Fibonacci numbers • Recall definition of Fibonacci numbers: f(0) = 0 f(1) = 1 f(n) = f(n-1) + f(n-2) • Computing the nth Fibonacci number recursively (top-down): f(n) f(n-1) f(n-2) + + f(n-3) . . . f(n-2) f(n-3) + f(n-4)

Example: Fibonacci numbers Computing the nth fibonacci number using bottom-up iteration: • f(0) = 0 • f(1) = 1 • f(2) = 0+1 = 1 • f(3) = 1+1 = 2 • f(4) = 1+2 = 3 • f(5) = 2+3 = 5 • • f(n-2) = • f(n-1) = • f(n) = f(n-1) + f(n-2) ALGORITHM Fib(n) F[0] 0, F[1] 1 for i 2 to n do F[i] F[i-1] + F[i-2] return F[n] extra space

Examples of Dynamic Programming § § § Computing binomial coefficients Compute the longest common subsequence Compute the shortest common supersquence Warshall’s algorithm for transitive closure Floyd’s algorithms for all-pairs shortest paths Some instances of difficult discrete optimization problems: § knapsack

Computing Binomial Coefficients n n n A binomial coefficient, denoted C(n, k), is the number of combinations of k elements from an n-element set (0 ≤ k ≤ n). Recurrence relation (a problem 2 overlapping subproblems) n C(n, k) = C(n-1, k-1) + C(n-1, k), for n > k > 0, and n C(n, 0) = C(n, n) = 1 Dynamic programming solution: n Record the values of the binomial coefficients in a table of n+1 rows and k+1 columns, numbered from 0 to n and 0 to k respectively. 1 1 1 … 1 2 3 4 5 1 3 6 10 1 4 10 1 5 1

Dynamic Binomial Coefficient Algorithm for i = 0 to n do for j = 0 to minimum( i, k ) do if j = 0 or j = i then Bi. Coeff[ i, j ] = 1 else Bi. Coeff[ i, j ] = Bi. Coeff[ i-1, j-1 ] + Bi. Coeff[ i-1, j ] end if end for j end for i

Longest Common Subsequence (LCS) n n A subsequence of a sequence S is obtained by deleting zero or more symbols from S. For example, the following are all subsequences of “president”: pred, sdn, predent. The longest common subsequence problem is to find a maximum length common subsequence between two sequences.

LCS For instance, Sequence 1: president Sequence 2: providence Its LCS is priden. president providence

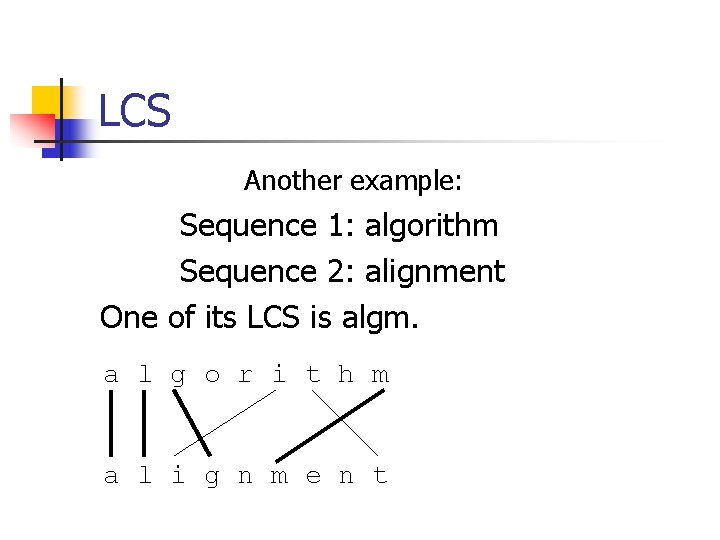
LCS Another example: Sequence 1: algorithm Sequence 2: alignment One of its LCS is algm. a l g o r i t h m a l i g n m e n t

How to compute LCS? n n n Let A=a 1 a 2…am and B=b 1 b 2…bn. len(i, j): the length of an LCS between a 1 a 2…ai and b 1 b 2…bj With proper initializations, len(i, j) can be computed as follows.

Running time and memory: O(mn) and O(mn).

The backtracing algorithm

Shortest common super-sequence n n n Definition: Let X and Y be two sequences. A sequence Z is a super-sequence of X and Y if both X and Y are subsequence of Z. Shortest common super-sequence problem: Input: two sequences X and Y. Output: a shortest common super-sequence of X and Y. Example: X=abc and Y=abb. Both abbc and abcb are the shortest common super-sequences for X and Y.

How to compute SCS? Recursive Equation: n Let len[i, j] be the length of an SCS of X[1. . . i] and Y[1. . . j]. n len[i, j] can be computed as follows: j i len[i, j] = len[i-1, j-1]+1 min{len[i, j-1]+1, len[i-1, j]+1} if i=0, if j=0, if i, j>0 and xi=yj, if i, j>0 and xi yj.

Solution: ABDCABDAB

Exercise n Consider the algorithm for LCS as an example, write down the SCS algorithm and analyze it.

An interesting example: Investment Problem Suppose there are m dollars，and n products. Let fi(x) be the profit of investing x dollars to product i. How to arrange the investment such that the total profit f 1(x 1) + f 2(x 2) + … + fn(xn) is maximized. Instance： 5 thousand dollars，4 products x 0 f 1(x) 0 f 2(x) 0 f 3(x) 0 f 4(x) 0 1 11 0 2 20 2 12 5 10 21 3 13 10 30 22 4 14 15 32 23 5 15 20 40 24

• Fk(x) optimum profit for investing x thousand dollars into producing the first k products. • xk(x) dollars invested on product k in Fk(x) Dynamic Programming Table x F 1(x) x 1(x) F 2(x) 1 11 0 20 1 2 12 0 13 1 31 1 3 13 3 16 2 30 3 33 1 4 14 4 21 3 41 3 50 1 5 15 5 26 4 43 4 61 1 Solution: x 1 =1, x 2(x) F 3(x) x 2 =0, x 3=3, x 3(x) F 4(x) x 4 =1 x 4(x) F 4(5) = 61

Algorithm for Investment n n n for y 1 to m F 1(y)=f 1(y) for k 2 to n for y 1 to m Fk(y) max 0<=xk<=y{fk(xk)+Fk-1(y-xk)} return Fn(m)

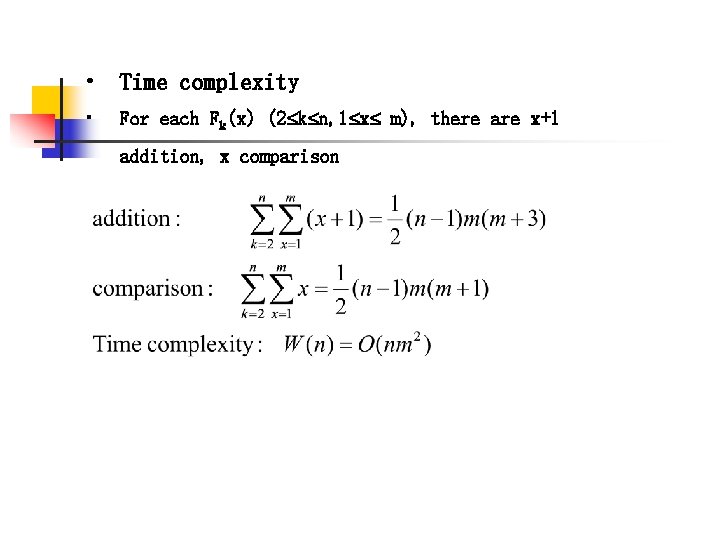
• Time complexity • For each Fk(x) (2 k n, 1 x m), there are x+1 addition, x comparison