Dynamic Programming CSCI 385 Data Structures Analysis of

Dynamic Programming CSCI 385 Data Structures & Analysis of Algorithms Lecture note Sajedul Talukder

Dynamic Programming Idea • You are given a box of coins and you have to count the total number of coins in it. • Now, you are provided with another box and now you have to calculate the total number of coins in both boxes. Total = 91 coins Don’t count the number of coins in the first box again

Dynamic Programming • An approach to problem solving that decomposes a large problem into a number of smaller problems for finding optimal solution. • Used for problems that are in multistage in nature. • No standard mathematical formulation, just store the values of the already calculated results. • But are we sacrificing anything for the speed? Yes, memory. Dynamic programming basically trades time with memory. Thus, we should take care that not an excessive amount of memory is used while storing the solutions.

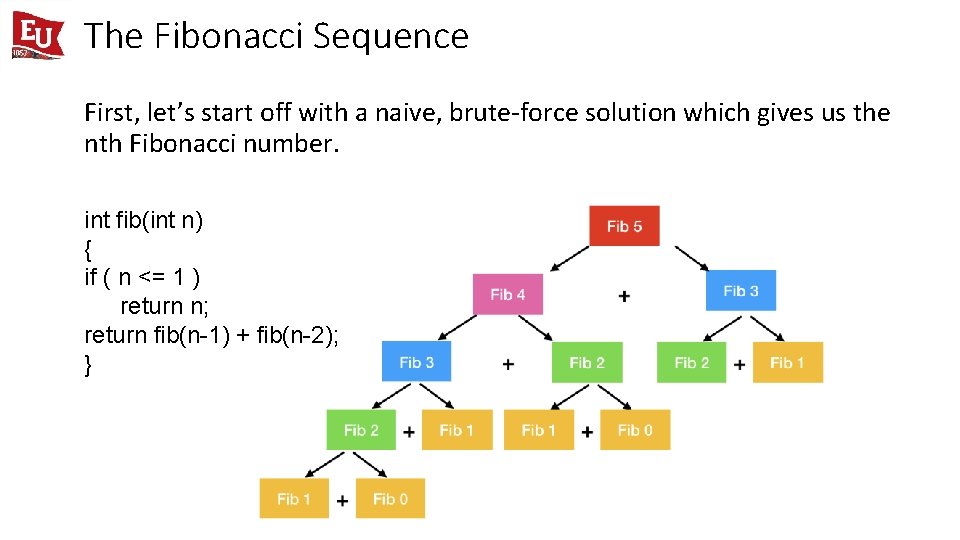
The Fibonacci Sequence First, let’s start off with a naive, brute-force solution which gives us the nth Fibonacci number. int fib(int n) { if ( n <= 1 ) return n; return fib(n-1) + fib(n-2); }

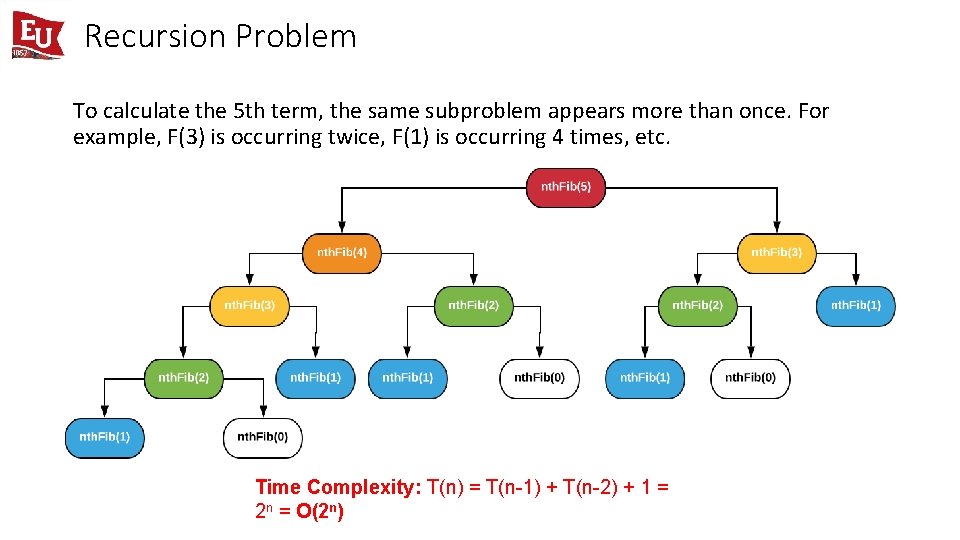
Recursion Problem To calculate the 5 th term, the same subproblem appears more than once. For example, F(3) is occurring twice, F(1) is occurring 4 times, etc. Time Complexity: T(n) = T(n-1) + T(n-2) + 1 = 2 n = O(2 n)

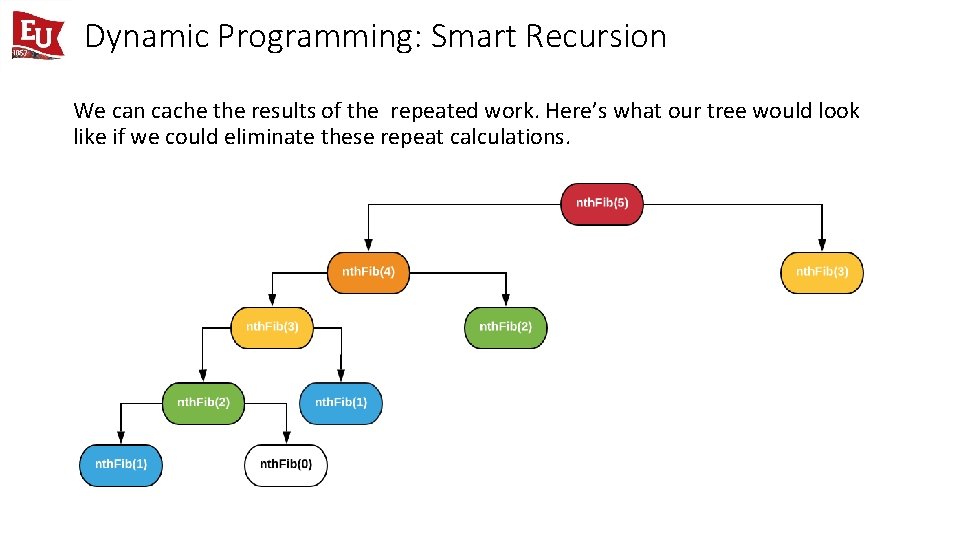
Dynamic Programming: Smart Recursion We can cache the results of the repeated work. Here’s what our tree would look like if we could eliminate these repeat calculations.

DP Properties • The reason we’ve eliminated so much of the tree is because we are checking our cache each time to see if some work has already been done. If it has, we simply return the value. If not, as is the case of our first branch, we run the calculation. • This simple change is the difference between an exponential time complexity and a linear time complexity. • Following are the two main properties of a problem that suggest that the given problem can be solved using Dynamic Programming. • Optimal Substructure • Overlapping Subproblems

Optimal Substructure • The first thing we need in a dynamic programming problem is optimal substructure. • Optimal substructure indicates that the optimal solution for our current problem can be constructed from the optimal solution to subproblems. For example: Fib(n) = Fib(n-1) + Fib(n-2). • Like Divide and Conquer, Dynamic Programming also combines solutions to sub-problems. • In dynamic programming, computed solutions to subproblems are stored in a table so that these don’t have to recomputed.

Overlapping Subproblems • The second prerequisite is overlapping subproblems. This implies that we have some sort of repeated work. • Dynamic Programming is mainly used when solutions of same subproblems are needed again and again. • Even with a small tree, it’s amazing how much work is unnecessary. Imagine how many Fib(2) calculations we would have for a problem like Fib(100). • Dynamic Programming is not useful when there are no common (overlapping) subproblems because there is no point storing the solutions if they are not needed again.

Memoization vs Tabulation • Dynamic Programming is an algorithmic paradigm that solves a given complex problem by breaking it into simple subproblems and stores the results of subproblems to avoid computing the same results again. • Memoization is an optimization technique used to speed up programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again. • Tabulation is an approach where you solve a dynamic programming problem by first filling up a table, and then compute the solution to the original problem based on the results in this table. 9

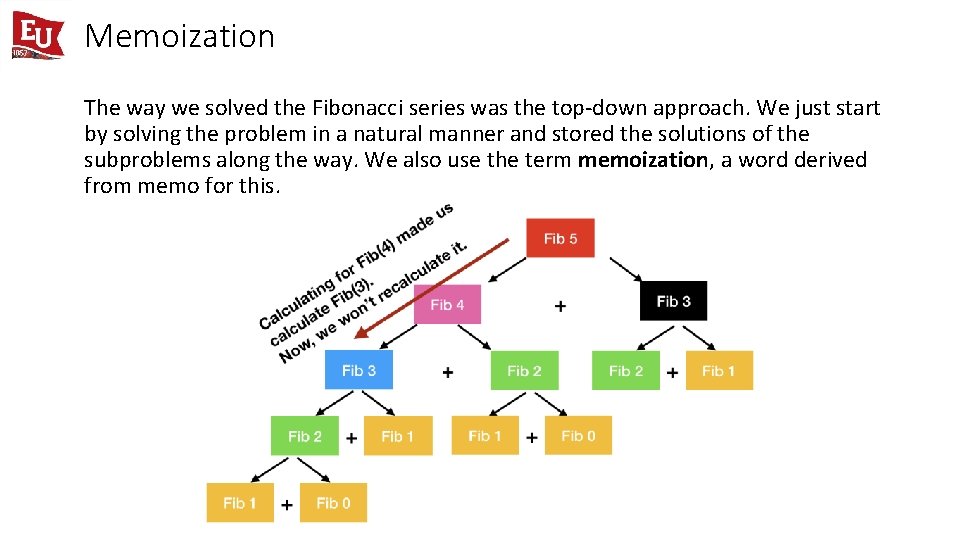
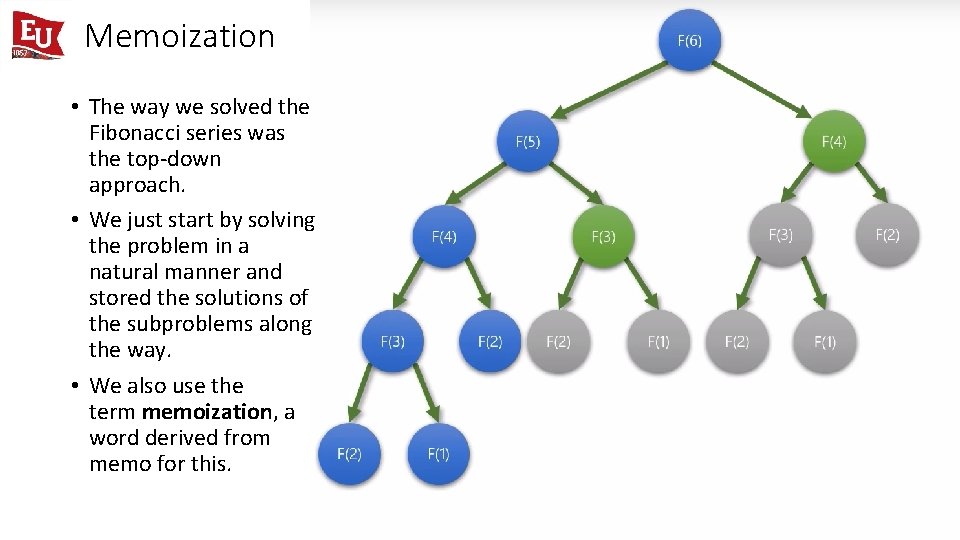
Memoization The way we solved the Fibonacci series was the top-down approach. We just start by solving the problem in a natural manner and stored the solutions of the subproblems along the way. We also use the term memoization, a word derived from memo for this.

Memoization • The way we solved the Fibonacci series was the top-down approach. • We just start by solving the problem in a natural manner and stored the solutions of the subproblems along the way. • We also use the term memoization, a word derived from memo for this.

Memoization Steps • We can use a global array or a lookup table of size N+1 to store the solution of the different sub-problems. let's say F[N+1]. • Initialize all the values in the array to -1 (As the value of Fibonacci can’t be negative). This could help us to check whether the solution of the sub-problem has been already computed or not. • We can do the following modification in the recursive solution: • If(F[N] < 0), it means the value of Fibonacci of N has not been computed yet. We need to calculate the solution recursively and store it at the Nth index of the table F[N] = fib(N-1) + fib(N-2). • If (F[N] > 0), then just return the value stored at F[N] (Because we have already computed the F[N] during the recursion). • N= 0 and N=1 are the base cases because we already know the value for this and we can directly store the solution at F[0] and F[1].

Memoization Code Initialize an array F[N+1] with negative values. int fib(int N) { if( F[N] < 0 ) { if( N <= 1 ) F[N] = N else F[N] = fib(N-1) + fib(N-2) } return F[N] }

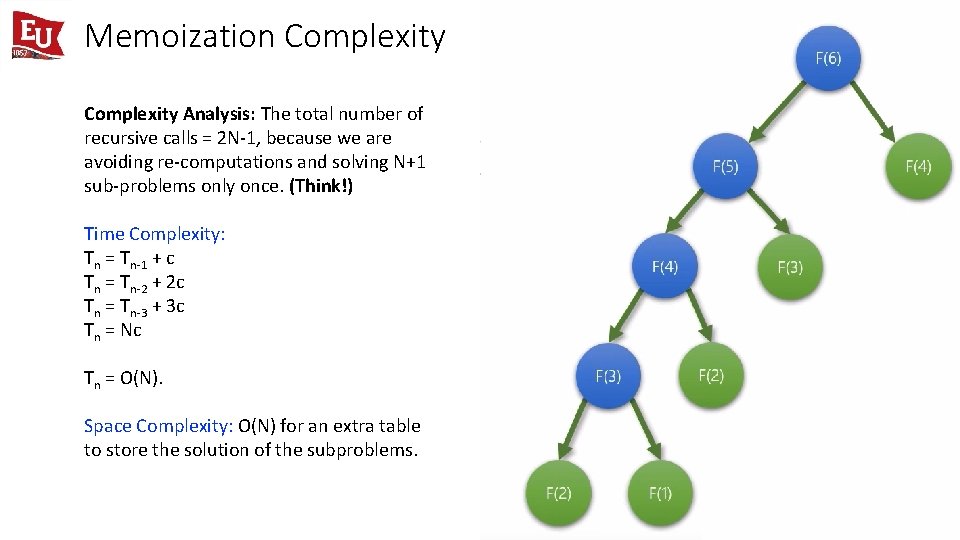
Memoization Complexity Analysis: The total number of recursive calls = 2 N-1, because we are avoiding re-computations and solving N+1 sub-problems only once. (Think!) Time Complexity: Tn = Tn-1 + c Tn = Tn-2 + 2 c Tn = Tn-3 + 3 c Tn = Nc Tn = O(N). Space Complexity: O(N) for an extra table to store the solution of the subproblems.

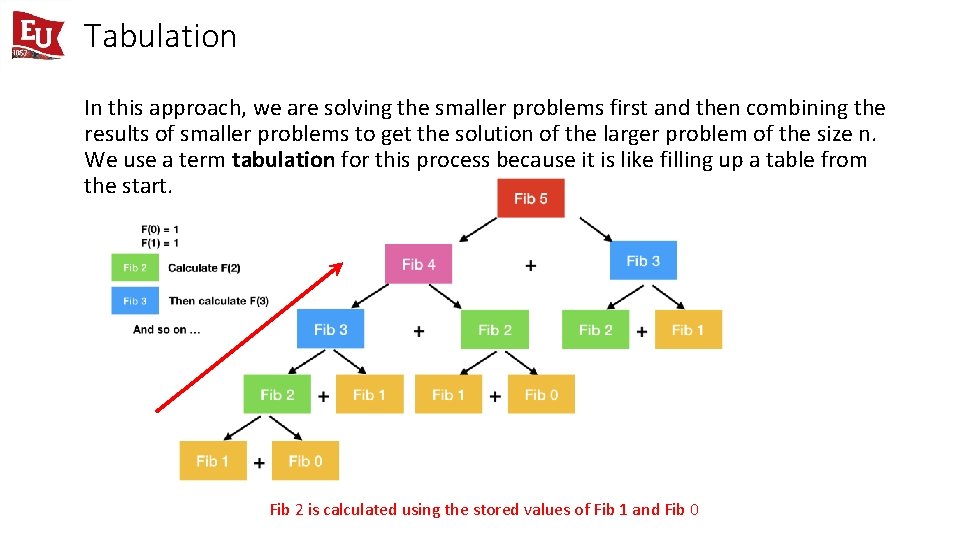
Tabulation In this approach, we are solving the smaller problems first and then combining the results of smaller problems to get the solution of the larger problem of the size n. We use a term tabulation for this process because it is like filling up a table from the start. Fib 2 is calculated using the stored values of Fib 1 and Fib 0

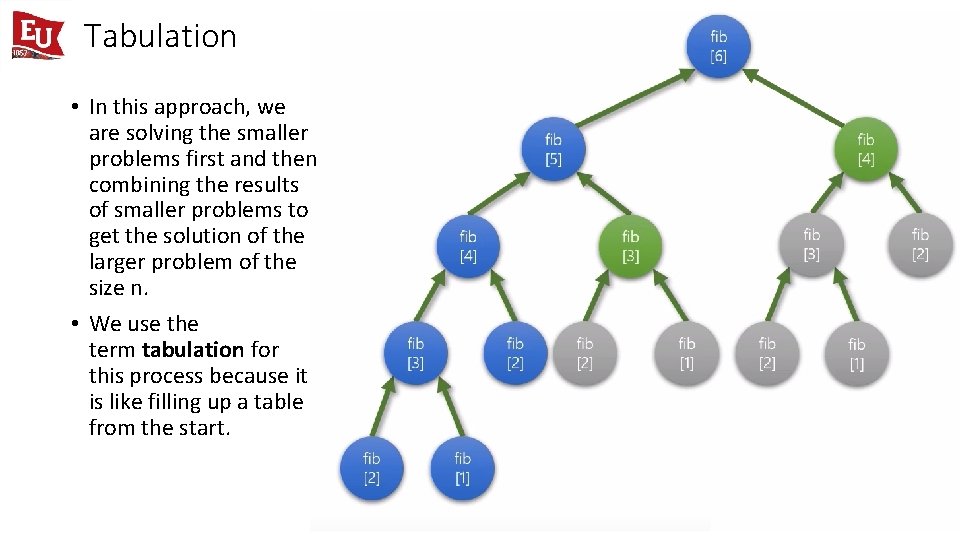
Tabulation • In this approach, we are solving the smaller problems first and then combining the results of smaller problems to get the solution of the larger problem of the size n. • We use the term tabulation for this process because it is like filling up a table from the start.

Tabulation Steps • Define Table Structure and Size: To store the solution of smaller sub-problems in a bottom-up approach, we need to define the table structure and its size. • Table Structure: The table structure is defined by the number of problem variables. Here we have only one variable on which the state of the problem depends i. e. which is n here. (The value of n is decreasing after every recursive call). So, we can construct a one-dimensional array to store the solution of the sub-problems. • Table Size: The size of this table is defined by the total number of different subproblems. If we observe the recursion tree, there can be total (n+1) sub-problems of different sizes. (Think!) • Initialize the table with the base case: We can initialize the table by using the base cases. This could help us to fill the table and build the solution for the larger sub-problem. F[0] = 0 and F[1] = 1 • Iterative Structure to fill the table: We should define the iterative structure to fill the table by using the recursive structure of the recursive solution. • Recursive Structure: fib(n) = fib(n-1) + fib(n-2) • Iterative structure: F[i] = F[i-1] + F[i-2] • Termination and returning final solution: After storing the solution in a bottom-up manner, our final solution gets stored at the last Index of the array i. e. return F[N].

Tabulation Code int F[N+1] // array(memory to store results) int fib(int N) { F[0] = 0 // base cases F[1] = 1 // base cases for( i = 2 to N ) F[i] = F[i-1] + F[i-2] return F[N] }

Tabulation Complexity Analysis: Similar as memorization approach! Time Complexity: O(N). Space Complexity: O(N) for an extra table to store the solution of the subproblems.

Memoization vs Tabulation • Ease of Coding - Memoization is easy to code i. e. you just add an array or a lookup table to store down the results and never recomputes the result of the same problem. But in the tabulation, you have to come up with ordering or iterative structure to fill the table. • Speed - Memoization can be slower than tabulation because of large recursive calls. • Stack Space - With memoization, if the recursion tree is very deep, you will run out of stack space, which will crash your program. • Subproblem Solving - In Tabulation, all subproblems must be solved at least once but in Memoization, all problems need not be solved at all, the memoized solution has the advantage of solving those sub-problems that are definitely required.

The general approach • Define your subproblem. • Break down your original problem into smaller parts. • Look for subproblems which are trivial or have obvious solutions. • Define relation between subproblem solutions. • Try defining a relation between the trivial/obvious subproblem and the next trivial/obvious subproblem. • Define the recurrence relationship which solves the actual problem. • Generalize the relation you found for N. • Write a DP algorithm for recurrence relation. • Apply memoization, or, • Do Tabulation. • Time complexity = (Number of Subproblems to actually solve ) x (Time taken to solve a subproblem)