Dynamic programming algorithms for allpairs shortest path and

Dynamic programming algorithms for all-pairs shortest path and longest common subsequences • We will study a new technique—dynamic programming algorithms (typically for optimization problems) • Ideas: – Characterize the structure of an optimal solution – Recursively define the value of an optimal solution – Compute the value of an optimal solution in a bottomup fashion (using matrix to compute) – Backtracking to construct an optimal solution from computed information. 1

Floyd-Warshall algorithm for shortest path: • Use a different dynamic-programming formulation to solve the all-pairs shortest-paths problem on a directed graph G=(V, E). • The resulting algorithm, known as the Floyd. Warshall algorithm, runs in O (V 3) time. – negative-weight edges may be present, – but we shall assume that there are no negativeweight cycles. 2

The structure of a shortest path: • We use a new characterization of the structure of a shortest path • Different from that for matrix-multiplication-based all-pairs algorithms. • The algorithm considers the “intermediate” vertices of a shortest path, where an intermediate vertex of a simple path p=<v 1, v 2, …, vk> is any vertex in p other than v 1 or vk, that is, any vertex in the set {v 2, v 3, …, vk-1} 3

Continue: • Let the vertices of G be V={1, 2, …, n}, and consider a subset {1, 2, …, k} of vertices for some k. • For any pair of vertices i, j V, consider all paths from i to j whose intermediate vertices are all drawn from {1, 2, …, k}, and let p be a minimum-weight path from among them. • The Floyd-Warshall algorithm exploits a relationship between path p and shortest paths from i to j with all intermediate vertices in the set {1, 2, …, k-1}. 4

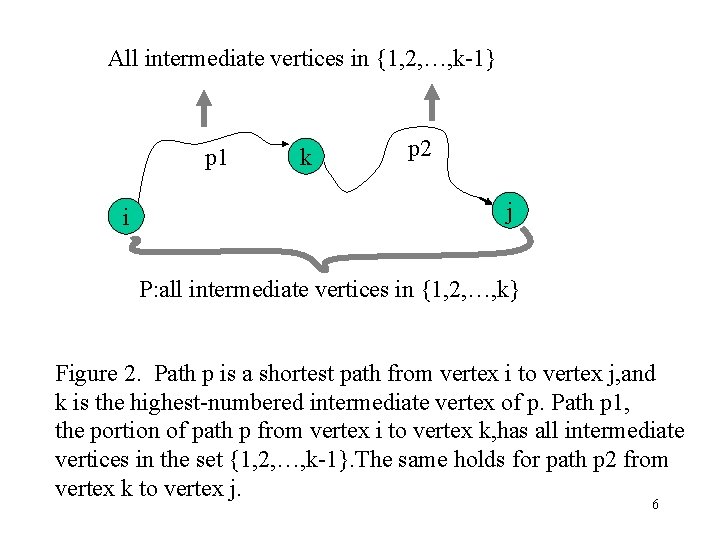
Relationship: • The relationship depends on whether or not k is an intermediate vertex of path p. • Case 1: k is not an intermediate vertex of path p – Thus, a shortest path from vertex i to vertex j with all intermediate vertices in the set {1, 2, …, k-1} is also a shortest path from i to j with all intermediate vertices in the set {1, 2, …, k}. • Case 2: k is an intermediate vertex of path p – we break p down into i k j as shown Figure 2. – p 1 is a shortest path from i to k with all intermediate vertices in the set {1, 2, …, k-1}, so is p 2. 5

All intermediate vertices in {1, 2, …, k-1} p 1 i k p 2 j P: all intermediate vertices in {1, 2, …, k} Figure 2. Path p is a shortest path from vertex i to vertex j, and k is the highest-numbered intermediate vertex of p. Path p 1, the portion of path p from vertex i to vertex k, has all intermediate vertices in the set {1, 2, …, k-1}. The same holds for path p 2 from vertex k to vertex j. 6

A recursive solution to the allpairs shortest paths problem: • Let dij(k) be the weight of a shortest path from vertex i to vertex j with all intermediate vertices in the set {1, 2, …, k}. A recursive definition is given by • dij(k)= wij if k=0, • min(dij(k-1), dik(k-1)+dkj(k-1)) if k 1. • The matrix D(n)=(dij(n)) gives the final answer-dij(n)= for all i, j V-because all intermediate vertices are in the set {1, 2, …, n}. 7

Computing the shortest-path weights bottom up: • • FLOYD-WARSHALL(W) n rows[W] D(0) W for k 1 to n do for i 1 to n do for j 1 to n dij(k) min(dij(k-1), dik(k-1)+dkj(k-1)) • return D(n) 8

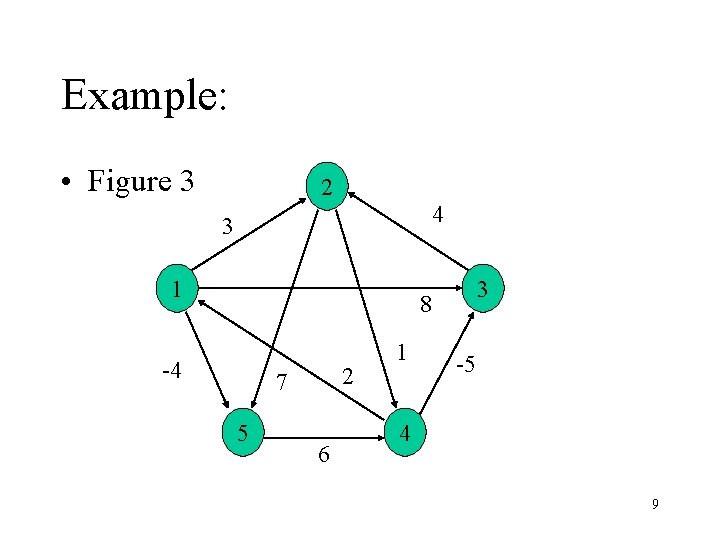
Example: • Figure 3 2 4 3 1 3 8 -4 2 7 5 6 1 -5 4 9

D(0)= D(1)= (0)= (1)= 10

D(2)= D(3)= (2)= (3)= 11

D(4)= D(5)= (4)= (5)= 12

Longest common subsequence • Definition 1: Given a sequence X=x 1 x 2. . . xm, another sequence Z=z 1 z 2. . . zk is a subsequence of X if there exists a strictly increasing sequence i 1 i 2. . . ik of indices of X such that for all j=1, 2, . . . k, we have xij=zj. • Example 1: If X=abcdefg, Z=abdg is a subsequence of X. X=abcdefg, Z=ab d g 13

• Definition 2: Given two sequences X and Y, a sequence Z is a common subsequence of X and Y if Z is a subsequence of both X and Y. • Example 2: X=abcdefg and Y=aaadgfd. Z=adf is a common subsequence of X and Y. X=abc defg Y=aaaadgfd Z=a d f 14

• Definition 3: A longest common subsequence of X and Y is a common subsequence of X and Y with the longest length. (The length of a sequence is the number of letters in the seuqence. ) • Longest common subsequence may not be unique. • Example: abcd acbd Both acd and abd are LCS. 15

Longest common subsequence problem • Input: Two sequences X=x 1 x 2. . . xm, and Y=y 1 y 2. . . yn. • Output: a longest common subsequence of X and Y. • A brute-force approach Suppose that m n. Try all subsequence of X (There are 2 m subsequence of X), test if such a subsequence is also a subsequence of Y, and select the one with the longest length. 16

Charactering a longest common subsequence • Theorem (Optimal substructure of an LCS) • Let X=x 1 x 2. . . xm, and Y=y 1 y 2. . . yn be two sequences, and • Z=z 1 z 2. . . zk be any LCS of X and Y. • 1. If xm=yn, then zk=xm=yn and Z[1. . k-1] is an LCS of X[1. . m-1] and Y[1. . n-1]. • 2. If xm yn, then zk xm implies that Z is an LCS of X[1. . m-1] and Y. • 2. If xm yn, then zk yn implies that Z is an LCS of X and Y[1. . n-1]. 17

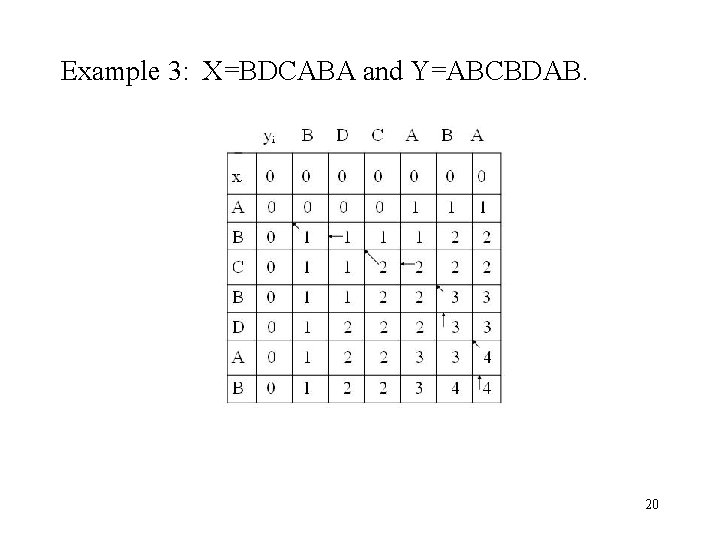
The recursive equation • Let c[i, j] be the length of an LCS of X[1. . . i] and X[1. . . j]. • c[i, j] can be computed as follows: 0 if i=0 or j=0, c[i, j]= c[i-1, j-1]+1 if i, j>0 and xi=yj, max{c[i, j-1], c[i-1, j]} if i, j>0 and xi yj. Computing the length of an LCS • There are n m c[i, j]’s. So we can compute them in a specific order. 18

The algorithm to compute an LCS • • • • 1. for i=1 to m do 2. c[i, 0]=0; 3. for j=0 to n do 4. c[0, j]=0; 5. for i=1 to m do 6. for j=1 to n do 7. { 8. if x[I] ==y[j] then 9. c[i, j]=c[i-1, j-1]=1; 10 b[i, j]=1; 11. else if c[i-1, j]>=c[i, j-1] then 12. c[i, j]=c[i-1, j] 13. b[i, j]=2; 14. else c[i, j]=c[i, j-1] 15. b[i, j]=3; 14 } 19

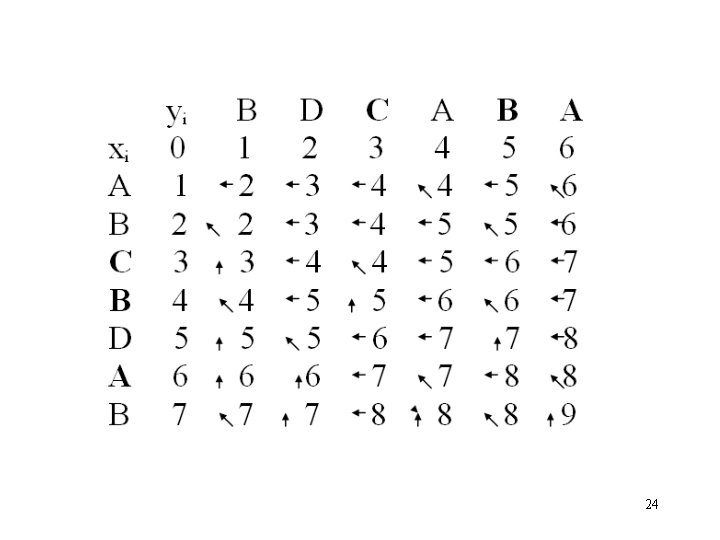
Example 3: X=BDCABA and Y=ABCBDAB. 20

Constructing an LCS (back-tracking) • We can find an LCS using b[i, j]’s. • We start with b[n, m] and track back to some cell b[0, i] or b[i, 0]. • The algorithm to construct an LCS 1. 2. 3. 4. i=m j=n; if i==0 or j==0 then exit; if b[i, j]==1 then { i=i-1; j=j-1; print “xi”; } 5. if b[i, j]==2 i=i-1 6. if b[i, j]==3 j=j-1 7. Goto Step 3. • The time complexity: O(nm). 21

Shortest common supersequence • Definition: Let X and Y be two sequences. A sequence Z is a supersequence of X and Y if both X and Y are subsequence of Z. • Shortest common supersequence problem: Input: Two sequences X and Y. Output: a shortest common supersequence of X and Y. • Example: X=abc and Y=abb. Both abbc and abcb are the shortest common supersequences for X and Y. 22

Recursive Equation: • Let c[i, j] be the length of an LCS of X[1. . . i] and X[1. . . j]. • c[i, j] can be computed as follows: c[i, j]= j if i=0 i if j=0, c[i-1, j-1]+1 if i, j>0 and xi=yj, min{c[i, j-1]+1, c[i-1, j]+1} if i, j>0 and xi yj. 23

24