Dynamic Programming Algorithmic Strategies Divide and Conquer Greedy

Dynamic Programming

Algorithmic Strategies • Divide and Conquer • Greedy Approach • Dynamic Programming

Algorithm Strategies: Key Differences • Divide and Conquer – Divide a problem into “disjoint” sub-problems – Solve the sub-problems first (bottom-up solution) – Combine the results somehow • Greedy Approach – Apply a greedy choice first – The choice will create sub-problems to solve (top-down solution) – Hopefully, local optimal will lead to global optimal

Algorithm Strategies: Key Differences (Cont’d) • Dynamic Programming – Divide a problem into sub-problems – Solve the sub-problems first, and then combine them to solve larger problem (bottom-up solution) Uses more space to save time – The sub-problems are overlapping • Divide and conquer will solve the same sub-problem again ad again • Dynamic programming will solve each sub-problem once, and remembers the answer – Similar to Greedy approach, it solves optimization problems

Dynamic Programming • Trades space (to save the sub-problems solutions) to save time • Can reduce exponential-time complexity to polynomial because of this extra storage • Tries to search all possible combinations. At each step it will select the best combination for each sub-problem

Rod Cutting

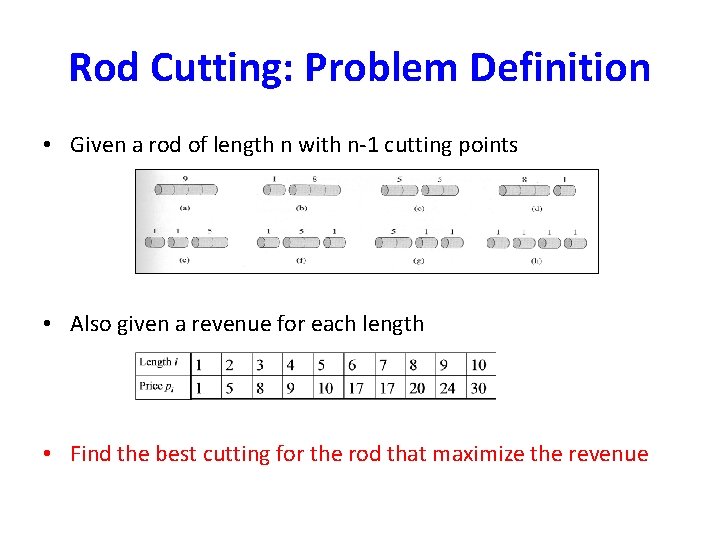
Rod Cutting: Problem Definition • Given a rod of length n with n-1 cutting points • Also given a revenue for each length • Find the best cutting for the rod that maximize the revenue

Example: Rod of size 4 • How many possible cuttings? – Exponential 2(n-1) = 23 = 8 • Each cutting point is a random variable (0 or 1) – We have n-1 cutting points – The total possibilities is 2(n-1) • Naïve Approach (exponential) – Try all possibilities and select the maximum – Best choice: Two pieces each of size 2 revenue = 5 + 5 = 10

Rod Cutting: Optimization Problem • Rod cutting is an optimization problem • Has the optimal sub-structure property – You must has the optimal cut for each sub-problem to get the global optimal • Has recursive exponential solution • Has polynomial dynamic programming solution

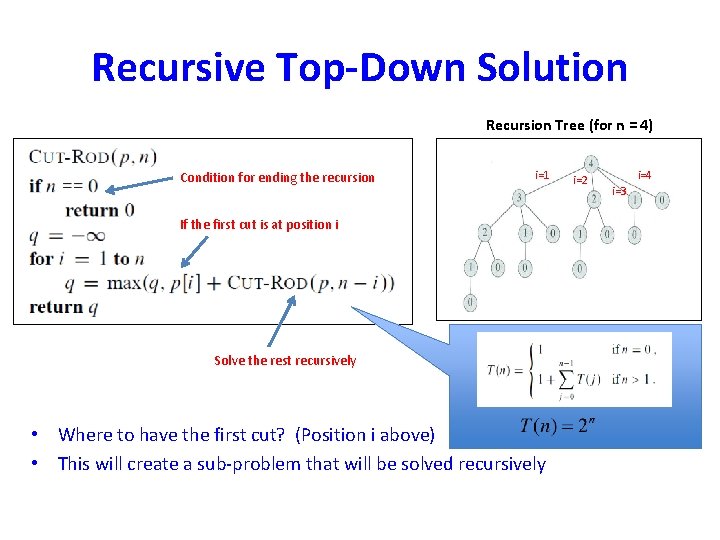
Recursive Top-Down Solution • Where to have the first cut? (Position i above) • This will create a sub-problem that will be solved recursively

Recursive Top-Down Solution Recursion Tree (for n = 4) Condition for ending the recursion i=1 If the first cut is at position i Solve the rest recursively • Where to have the first cut? (Position i above) • This will create a sub-problem that will be solved recursively i=2 i=4 i=3

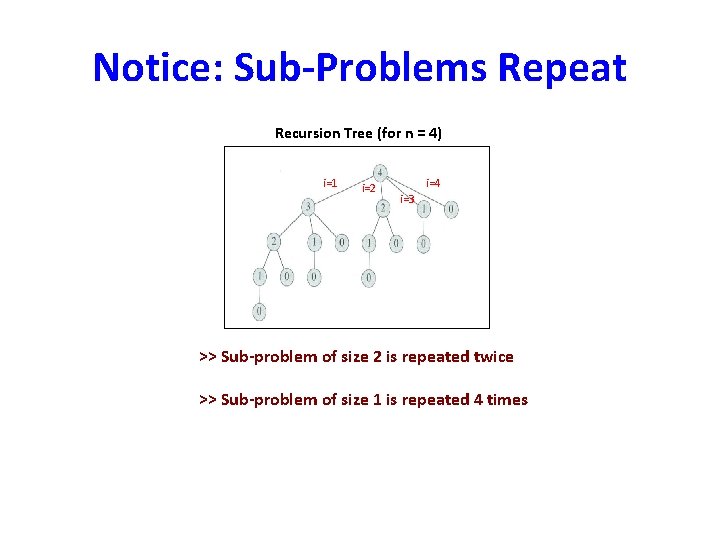
Notice: Sub-Problems Repeat Recursion Tree (for n = 4) i=1 i=2 i=4 i=3 >> Sub-problem of size 2 is repeated twice >> Sub-problem of size 1 is repeated 4 times

Dynamic Programming Solution • Store sub-problem results, don’t re-compute – Time vs. Memory trade-off • Turn a exponential-time solution into a polynomialtime solution

Version 1: Top-down with Memoization r[x] is the best revenue for size x If this size is solved before, just return its optimal solution Same as before (i is the first-cut position, the rest is solved recursively)

Version 2: Bottom-Up Without Recursion • Solve the sub-problems in order (smaller to larger) Size 0 has revenue 0 Increment the problem size by 1 each time This loop gets the maximum among all possible cuts All smaller sub-problems are already computed Time Complexity O( n 2) Space Complexity O(n)

Reconstructing The Optimal Solution • So far, the algorithm tells you the optimal revenue • But, does not tell how to get it Tells you for size 4, the optimal revenue is 10 !! • We need extra space Only store the 1 st-cut position for each size (not all positions) – S[4] = 2 // meaning the 1 st-cut position for size 4 is 2 – Now we have pieces, each of size 2 • To know their cut, go to S[2]

Code Extension Problem size Max revenue 1 st cut position