Dynamic Modeling and Stochastic Simulation of Metabolic Networks

Dynamic Modeling and Stochastic Simulation of Metabolic Networks Emalie Clement Dr. Paul Davis, Dr. Tadeusz Wysocki, Dr. Beata Wysocki Research and Creative Activity Fair March 2, 2018 1

Introduction ● Sugar = Glucose ● Essential in energy production and sustaining life ● Glucose metabolism disrupted in disease: cancer, diabetes ● Comprehension of “diseased” states 2

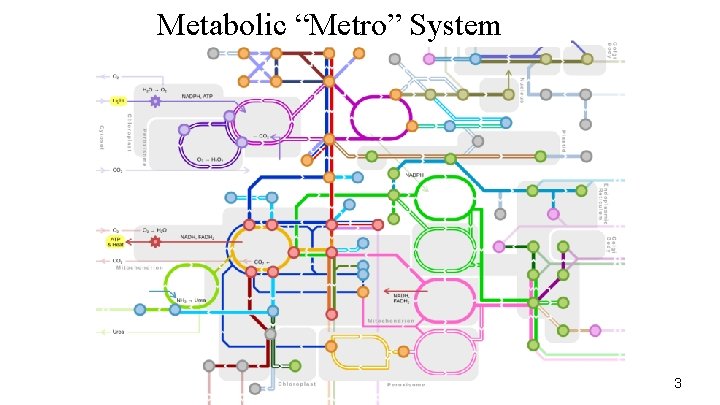
Metabolic “Metro” System 3

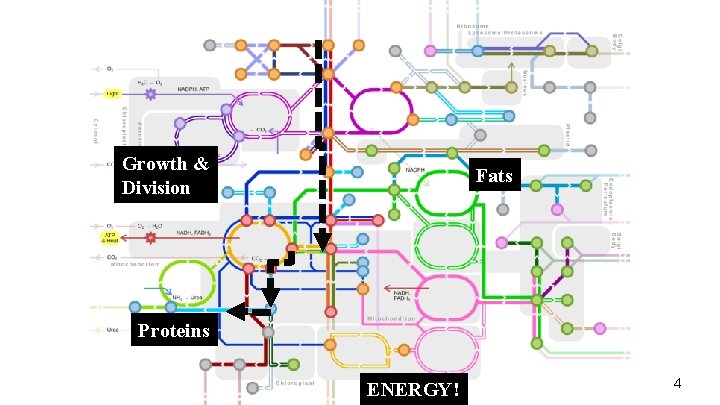
Growth & Division Fats Proteins ENERGY! 4

Human Metabolism Map 5

6

Why Model Biological Systems? ● Use computers to understand disease ● Goal: Represent real systems with computers by the currently known relationships ● Investigation of the characteristics of complex systems 7

Biological variation • Variation is inherent in biology. • Modeling variation is more realistic. 8

Modeling Random Variation ● Significantly more complicated ● Significant time increase 9

The Internet Goal: model cells like we model the internet. 10

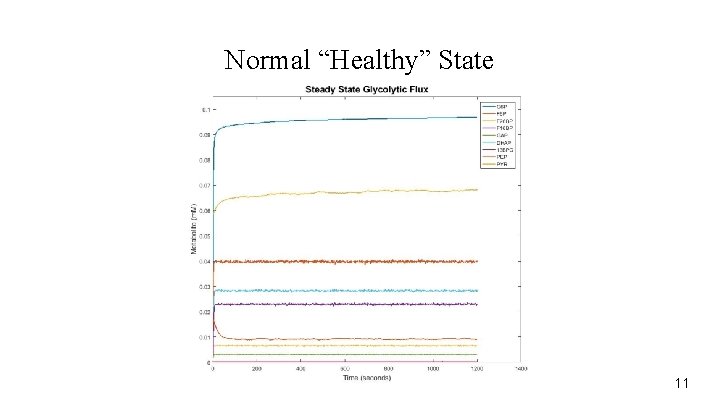
Normal “Healthy” State 11

Replicate Outcomes of Cancer Drugs ● FK 866 is under being tested as a potential caner treatment ● Inhibits Glucose metabolism ○ Treated cells with FK 866 ○ Ovarian cancer cell line ○ Colorectal cancer cell line 12

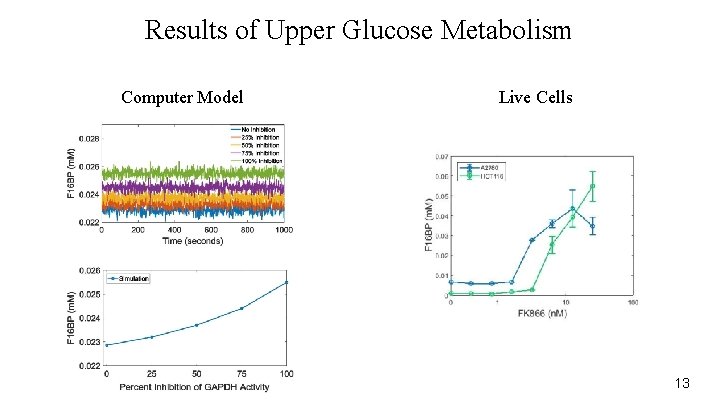
Results of Upper Glucose Metabolism Computer Model Live Cells 13

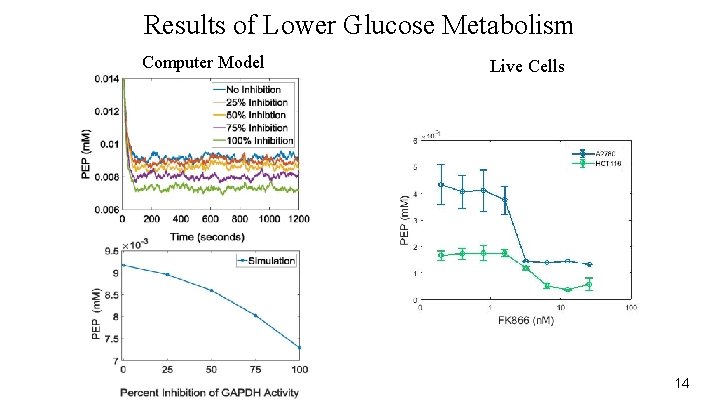
Results of Lower Glucose Metabolism Computer Model Live Cells 14

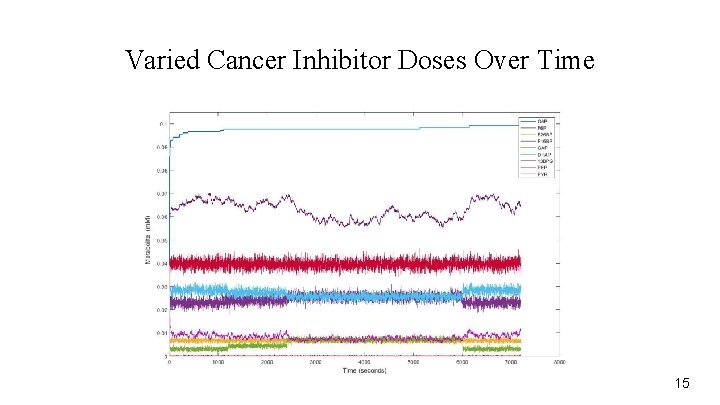
Varied Cancer Inhibitor Doses Over Time 15

Conclusion ● Modeling can help in understanding disease ● The model presented is an efficient method of modeling randomness that is seen in biological systems ● With better knowledge we can begin looking to treat, prevent, and even cure diseases 16

Thank You!!! 17

References [1] N. Tomar and R. De, “A Comprehensive View on Metabolic Pathway Analysis Methodologies, ” Curr. Bioinforma. , vol. 9, no. 3, pp. 295– 305, May 2014. [2] E. O. Voit, “The best models of metabolism: The best models of metabolism, ” Wiley Interdiscip. Rev. Syst. Biol. Med. , p. e 1391, May 2017. [3] S. K. Hahl and A. Kremling, “A Comparison of Deterministic and Stochastic Modeling Approaches for Biochemical Reaction Systems: On Fixed Points, Means, and Modes, ” Front. Genet. , vol. 7, Aug. 2016. [4] J. Wu, B. Vidakovic, and E. O. Voit, “Constructing stochastic models from deterministic process equations by propensity adjustment, ” BMC Syst. Biol. , vol. 5, no. 1, p. 187, 2011. [5] D. T. Gillespie, “Stochastic Simulation of Chemical Kinetics, ” Annu. Rev. Phys. Chem. , vol. 58, no. 1, pp. 35– 55, May 2007. [6] D. Guo et al. , “Endosomal trafficking of nanoformulated antiretroviral therapy facilitates drug particle carriage and HIV clearance, ” J. Virol. , vol. 88, no. 17, pp. 9504– 9513, Sep. 2014. [7] A. T. Sharp, A. K. Pannier, B. J. Wysocki, and T. A. Wysocki, “A novel telecommunications-based approach to HIV modeling and simulation, ” Nano Commun. Netw. , vol. 3, no. 2, pp. 129– 137, Jun. 2012. [8] T. Martin, B. Wysocki, T. Wysocki, and A. Pannier, “Identifying Intracellular p. DNA Losses From a Model of Nonviral Gene Delivery, ” IEEE Trans. Nanobioscience, Jan. 2015. [9] V. P. Evstigneev, M. G. Holyavka, S. V. Khrapatiy, and M. P. Evstigneev, “Theoretical description of metabolism using queueing theory, ” Bull. Math. Biol. , vol. 76, no. 9, pp. 2238– 2248, Sep. 2014. [10] A. J. Jezewski, J. J. Larson, B. Wysocki, P. H. Davis, and T. Wysocki, “A novel method for simulating insulin mediated GLUT 4 translocation, ” Biotechnol. Bioeng. , vol. 111, no. 12, pp. 2454– 2465, Dec. 2014. [11] B. Tan et al. , “Pharmacological Inhibition of Nicotinamide Phosphoribosyltransferase (NAMPT), an Enzyme Essential for NAD + Biosynthesis, in Human Cancer Cells: METABOLIC BASIS AND POTENTIAL CLINICAL IMPLICATIONS, ” J. Biol. Chem. , vol. 288, no. 5, pp. 3500– 3511, Feb. 2013. 18