Dynamic Lot Sizing 35 E 00100 Service Operations

Dynamic Lot Sizing 35 E 00100 Service Operations and Strategy #6 Fall 2015

Topics Demand management Lot sizing policies Order management Key points Useful material: Hopp, W. & Spearman, M. (2000), Factory Physics, Chapter 2. 1 -2. 4 and 3. 1. 6 Nahmias, S. (2002) “Alternative Lot Sizing Schemes” Ch 7. 2 in Production and Operations Analysis Vollmann, T. , W. Berry & C. Whybark (1997) “Mc. Laren’s Order Moment” in Manufacturing Planning and Control Systems 35 E 00100 Service Operations and Strategy #6 2 Aalto/BIZ Logistics

Demand management is a part of the MPC system! MPC boundary Resource planning Production planning Demand management Master production scheduling Marketplace (customers and other demand sources) Front end Engine Back end 35 E 00100 Service Operations and Strategy #6 3 Vollmann et al. 1997, 313 Aalto/BIZ Logistics

Need for capacity management depends on the market situation Sales forecasts Business plan FGI and Backlog Define production plan rates Orders Master schedule rough cut Approvals Master schedule Vollmann et al. 1997 35 E 00100 Service Operations and Strategy #6 4 Aalto/BIZ Logistics

Capacity and Demand Control Tools Ways to manage capacity n “Stretch” production capacity - Speed up the process - Schedule downtime (e. g. maintenance) during periods of low demand - Squeeze more people in or rent / share extra facilities equipment n Workforce management - Employ part-timers, seasonal workers, flexible work force - Cross-train employees - Prepare intelligent schedules for both workers and equipment Strategies for managing demand n Organize better - Avoid needless division of work (finance, customer service, transport planning, etc. ) - Design rules and procedures for providing flexibility n Manage service levels - Adjust delivery promises continuously - Utilize different pricing methods n Communicate capabilities 35 E 00100 Service Operations and Strategy #6 5 Aalto/BIZ Logistics

Lot Sizing Schemes 35 E 00100 Service Operations and Strategy #6 6 Aalto/BIZ Logistics

Example 1 Comparison of Lot Sizing Policies A component used in a manufacturing facility is ordered from an outside supplier. Because the component is used in a variety of end products, the demand is high. Estimated demand (in thousands) over the next 10 weeks is: Cost per component is 0. 65. The interest rate used to compute holding costs is 0. 5 % per week. The fixed ordering cost is estimated to be 200. n What ordering policy you recommend and why? n Which method would result in the lowest-cost policy for this problem? 35 E 00100 Service Operations and Strategy #6 7 Aalto/BIZ Logistics

Lot for Lot Ordering Basic principle of LFL n Production quantity = time-phased net requirements n No inventory carried from one period to another Normal assumption in MRP examples n For convenience and ease of use Rarely the optimal production rule 35 E 00100 Service Operations and Strategy #6 8 e. g. Hopp and Spearman 2000, 125 Aalto/BIZ Logistics

Economic Order Quantity (EOQ) The principle n Production quantity = EOQ quantity n Information required - Fixed setup/ ordering cost A - Holding cost h - Demand rate D Shortcomings are due to the assumptions of the modell n Instantaneous production n Immediate delivery n Deterministic and constant demand over time n Fixed setup cost n Products can be analyzed individually 35 E 00100 Service Operations and Strategy #6 9 e. g. Hopp and Spearman 2000, 49 -56 Aalto/BIZ Logistics

Periodic Order Quantity (POQ) The principle n Calculate the time between orders (TBO) using EOQ formula TBO = EOQ / D n TBO (rounded to closest integer) shows for how many periods products should be produced or ordered. Fixed order period (FOP) is a similar method. n Periods with no demand are skipped. 35 E 00100 Service Operations and Strategy #6 10 e. g. Hopp and Spearman 2000, 126 -127 Aalto/BIZ Logistics

Part Period Balancing (PPB) The principle n Definition of a part-period - [# of parts in a lot] * [# of period they are carried in inventory] n Combines the procedure of Wagner-Whitin with the mechanics of the EOQ - Set the order horizon equal to the number of periods that most closely matches the total holding cost with the set-up cost over that period n Steps of the procedure - Calculate holding costs per different number of periods - Compare when holding cost is closest to set-up costs - Stop and repeat 35 E 00100 Service Operations and Strategy #6 11 e. g. Hopp and Spearman 2000, 127 -128 Aalto/BIZ Logistics

Mc. Laren’s Order Moment (MOM) The principle n Evaluates the set-up cost for an integral number of future periods n Applies part period (=an unit of inventory carried for one period) accumulation principle directly n Lot size is determined by matching the number of accumulated part periods to the number that would be incurred if an order for an EOQ were placed under conditions of constant demand n Calculate order moment target (OMT) T* = largest integer less than or equal to TBO K = period currently under consideration rj = requirement/demand for period j n Two tests are used - Tentatively order covers the requirements of periods (r) for which - Once accumulated parts reach or exceed the OMT, test if one more period should be included 35 E 00100 Service Operations and Strategy #6 12 e. g. Vollman et al. 1997, 445 -446 Aalto/BIZ Logistics

Least Unit Cost (LUC) The principle n Choose order horizon that minimizes the cost per unit of demand n Define C(T) as the average holding and set-up cost per unit if the current order spans the next T periods n Let (r 1, …, rj) be the requirements over the j-period horizon -. -. 35 E 00100 Service Operations and Strategy #6 13 e. g. Nahmias 2001, 369 -370 Aalto/BIZ Logistics

Silver-Meal Heuristic (S-M) The principle n Minimize average cost period over T-period order horizon n Define C(T) as the average holding and set-up cost period if the current order spans the next T periods If we place an order in period 1, for… n r 1 : n r 2: n r 3: n In general rn: Once Cj > Cj-1 stop, and set Q 1 = r 1 + r 2 +…+ rj-1 and begin process again starting at period j 35 E 00100 Service Operations and Strategy #6 14 e. g. Nahmias 2001, 368 -369 Aalto/BIZ Logistics

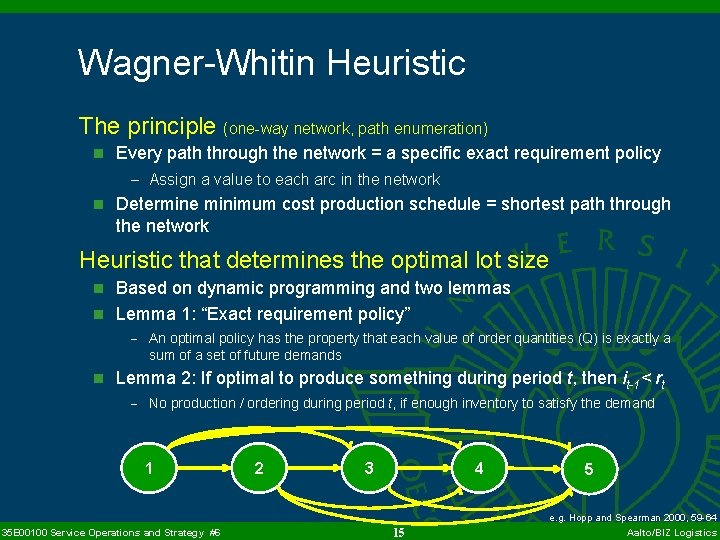
Wagner-Whitin Heuristic The principle (one-way network, path enumeration) n Every path through the network = a specific exact requirement policy - Assign a value to each arc in the network n Determine minimum cost production schedule = shortest path through the network Heuristic that determines the optimal lot size n Based on dynamic programming and two lemmas n Lemma 1: “Exact requirement policy” - An optimal policy has the property that each value of order quantities (Q) is exactly a sum of a set of future demands n Lemma 2: If optimal to produce something during period t, then it-1< rt - No production / ordering during period t, if enough inventory to satisfy the demand 1 35 E 00100 Service Operations and Strategy #6 2 3 4 15 5 e. g. Hopp and Spearman 2000, 59 -64 Aalto/BIZ Logistics

Example 1 Comparison of Lot Sizing Policies A component used in a manufacturing facility is ordered from an outside supplier. Because the component is used in a variety of end products, the demand is high. Estimated demand (in thousands) over the next 10 weeks is: Cost per component is 0. 65. The interest rate used to compute holding costs is 0. 5 % per week. The fixed ordering cost is estimated to be 200. n What ordering policy you recommend and why? n Which method would result in the lowest-cost policy for this problem? 35 E 00100 Service Operations and Strategy #6 16 Aalto/BIZ Logistics

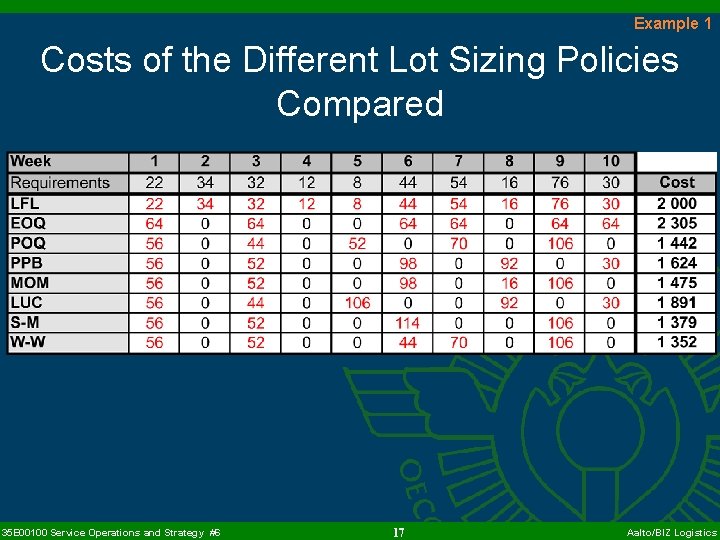
Example 1 Costs of the Different Lot Sizing Policies Compared 35 E 00100 Service Operations and Strategy #6 17 Aalto/BIZ Logistics

Example 1 Ranking of the Policies 1. 2. 3. 4. 5. 6. 7. 8. Wagner-Whitin (W-W) 1352 Silver-Meal (S-M) Periodic Order Quantity (POQ) Mc. Laren's Order Moment (MOM) Part Period Balancing (PPB) Least Unit Cost (LUC) Lot-for-Lot (LFL) 1379 1442 1475 1624 1891 2000 Economic Order Quantity (EOQ) 2305 35 E 00100 Service Operations and Strategy #6 18 Aalto/BIZ Logistics

Differences in Lot Sizing Policies Lot-for-lot n Cost estimation or calculation is not required n Least likely to result in capacity problems n Likely to cause high changeover costs (produced / ordered every period) EOQ n A simple calculation technique n Likely to produce cost-wise inefficient solutions if demand is not stable Wagner-Whitin n Gives the optimal solution for static problems at one level of the product structure - Under some other conditions the optimality is lost n Relatively much calculations required S-M, LUC, PPB, MOM n Similar methods that give a reasonable compromise between the simple LFL scheduling and the W-W heuristic n PPB is easiest in terms of calculations n S-M seems to provide the most cost effective solutions on average, and it involves less work than the W-W heuristic 35 E 00100 Service Operations and Strategy #6 19 Aalto/BIZ Logistics

Elements of Marketing Planning Capacity on cti ele Sc he t S du un lin co g Ac Orders 35 E 00100 Service Operations and Strategy #6 Forecasting 20 Customers Aalto/BIZ Logistics

Manufacturing-Marketing Collaboration 35 E 00100 Service Operations and Strategy #6 21 Shapiro 1977, 105 Aalto/BIZ Logistics

Why Orders Fall through the Cracks? 35 E 00100 Service Operations and Strategy #6 22 Shapiro et al. 1992, 105 Aalto/BIZ Logistics

Key Points Lot sizing policies n Consider the trade-off between holding inventory and changeover - By adjusting setup costs, the planner can trade inventory for capacity n Simple methods are popular in practice - People prefer to understand the solution - Heuristics are good because those are relatively robust and intuitive n Costs versus responsiveness Order management n Information sharing and incentive alignment important n Separate orders from customers 35 E 00100 Service Operations and Strategy #6 23 Aalto/BIZ Logistics

Abbreviations Used EOQ = economic order quantity FOP LUC MOM MRP OMT PPB POQ S-M TBO W-W = = = = = fixed order period least unit cost Mc. Laren’s order moment material requirements planning order moment target part period balancing periodic order quantity Silver-Meal heuristic time between orders Wagner-Whitin heuristic 35 E 00100 Service Operations and Strategy #6 24 Aalto/BIZ Logistics