Dynamic Data Structures for Simplicial Thickness Queries Danny

Dynamic Data Structures for Simplicial Thickness Queries Danny Z. Chen and Haitao Wang Computer Science and Engineering University of Notre Dame Indiana, USA

Outline n n Problem definitions Related work Our solutions Further discussions

Simplicial thickness n n Given: A set S of simplices in d-D space (d>1 is fixed), a point p The simplicial thickness of p: The number of simplices in S containing p 2 3 1

Simplicial thickness query n n Given: A set P of n points and a simplex set S in d-space (S=Ø initially) Objective: Design a data structure to support n n n Simplex insertion: Insert a simplex to S Simplex deletion: Delete a simplex from S Simplicial thickness query: Given a query simplexσ, report the point with the minimum simplicial thickness among all points inσ∩P

Related work n n No previous work on the problem Simplex range searching [Chazelle 90, Matousek 92, 93] Dynamic versions supporting point insertions and deletions [Matousek 92] Standard dynamic data structure design techniques [Overmars 83]

Our solution n We propose a data structure with the following bounds: n n n O(n logn) time and O(n) space Support the simplex insertion, deletion, simplicial thickness query in O(n 1 -1/d(logn)O(1)) time each (e. g. , n 1/2(log n)O(1) when d=2) Based on simplicial partitions [Matousek 92]

Simplicial partition [Matousek] n Given a point set P, its simplicial partition is ∏={(P 1, △ 1)…(Pm, △m)}: n n Pi’s are pairwise disjoint subsets which form a partition of P Each △i is a simplex containing Pi

Special simplicial partition n n We call a simplicial partition special if max{|Pi|}<2 min{|Pi|} Given a half-space: n n Easy: Process the points in the simplices which do not intersect its boundary Problem: How to handle those simplices intersecting its boundary?

Partition tree [Matousek] n For a point set P, build a partition tree T by constructing special simplicial partitions on P recursively: n n Each internal node v corresponds to a subset Pv, a simplex △v, and a special simplicial partition ∏v of Pv Each leave corresponds to a constant size subset

A partition tree

Time and space n T can be constructed in O(n logn) time and O(n) space [Matousek 92]

Our new data structure T’ n n n T’ is similar to T But, in addition, we also store two values k 1(v) and k 2(v) at each node v Some new concepts are needed

Poke n A simplex s pokes another simplex s’ if s∩s’≠Ø and s does not contain s’ completely blue pokes red also pokes blue pokes red

Intersection set (IS) n For each node v, define IS(v) as the set of simplices in IS(parent(v)) which poke △v (if v is the root, IS(v)=S)

Definitions of k 1(v) and k 2(v) n n n k 1(v): The number of simplices in IS(parent(v)) which contain △v completely (k 1(v)=0 if v is the root) k 2(v): The minimum simplicial thickness among all points in Pv with respect to the simplices in IS(v) For each point pi in a leaf node v, we also store k 1(pi) as the number of simplices in IS(v) which contain pi

Construction time and space n n O(n) space O(nlogn) time

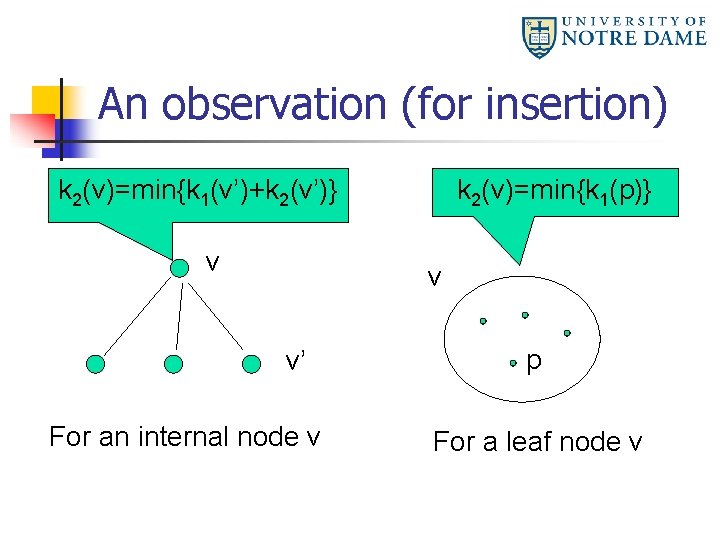
An observation (for insertion) k 2(v)=min{k 1(v’)+k 2(v’)} v k 2(v)=min{k 1(p)} v v’ For an internal node v p For a leaf node v

Simplex insertionσ n Update k 1 values: Beginning from the root, for each internal node v: n n n Ifσcontains △v, we increase k 1(v) by 1 If σpokes △v, we process all children of v recursively Update k 2 values: By the preceding observation

Simplex insertionσ(cont. ) n n The time complexity is O(n 1 -1/d(log n)O(1)) Simplex deletion can be handled analogously

An observation (for query) n n If we apply simplex insertion on the query simplexσ, the k 1 values of some nodes and points will be increased. We call those nodes and points the ending nodes

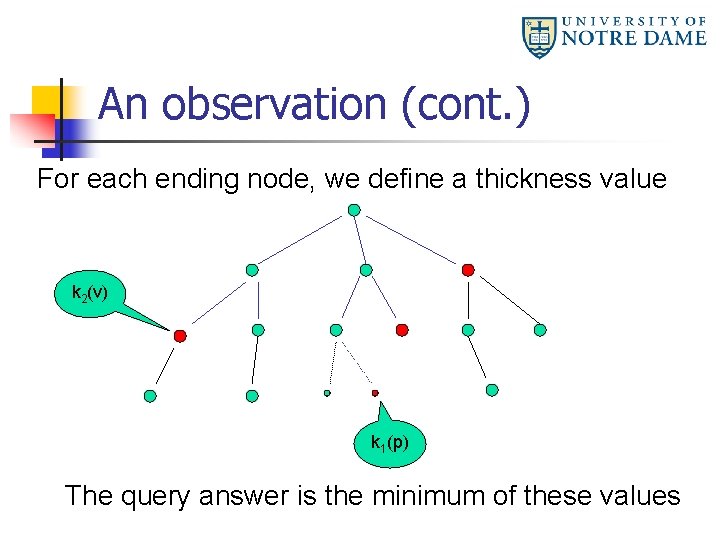
An observation (cont. ) For each ending node, we define a thickness value k 2(v) k 1(p) The query answer is the minimum of these values

Simplicial thickness queryσ n n n As we going down in the tree, we accumulate the sum of k 1 values from the root to the current node We also maintain the current minimum thickness value Query time is O(n 1 -1/d(log n)O(1))

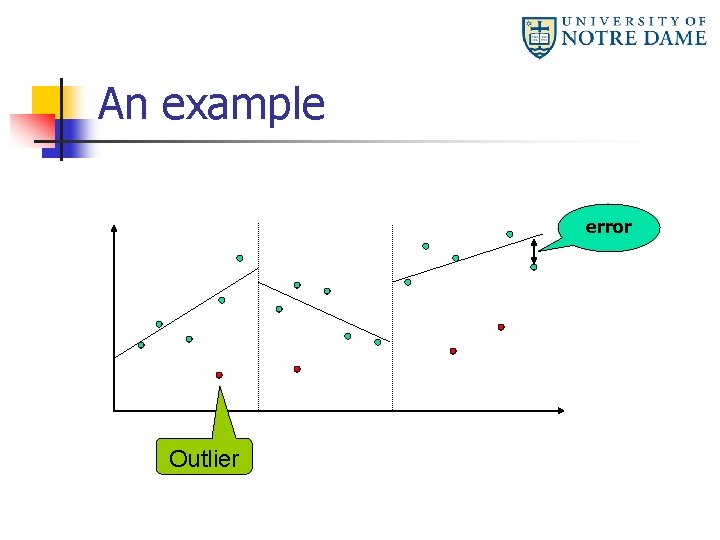
Applications Point approximation: n Input: A point set P in the plane, an integer g>0, andε>0 n Output: A piecewise linear function f to approximate P with g outliers, s. t. , n n n The complexity of f is minimized The maximum vertical point error is no more thanε The number of outliers is no more than g

An example error Outlier

A sub-problem Given P’ which is a subset of P, and an integer q (0≤q≤g) with P’=Ø initially, derive a data structure to support three operations: n Point insertion: Insert a point from PP’ to P’ n Point deletion: Delete a point from P’ n Feasibility test: Determine whethere exists a line segment to approximate the points in P’ with at most q violations and with error no more than the givenε

3 -D k-level lowest point query n n Given: A set P of n planes in 3 -D space, an integer k>0, a constantε>0, and P’ P Objective: A data structure to support the following operations n n n Plane insertion: Insert a plane of PP’ to P’ Plane deletion: Delete a plane from P’ k-level lowest point query: Determine whether the lowest point on the k-level of the plane arrangement of P’ has z-coordinate larger thanε

Further discussions n n Weighted version: Each simplex has a weight Max version: Query the point with the maximum simplicial thickness

Thank you