Dynamic Causal Modelling DCM for induced responses CC

Dynamic Causal Modelling (DCM) for induced responses CC Chen Wellcome Trust Centre for Neuroimaging Institute of Neurology, UCL, London Dr. James Kilnear , Dr. Stefan Kiebel, Prof. Karl Friston and Dr. Nick Ward

Contents • Evoked and Induced activities • Methods for frequency-based analyses • DCM for induced responses • One condition, Single subject result -- intrinsic nonlinearity and force modulation in motor system • Two conditions, group result -- functional asymmetries between forward and backward connections induced by face processing • Summary

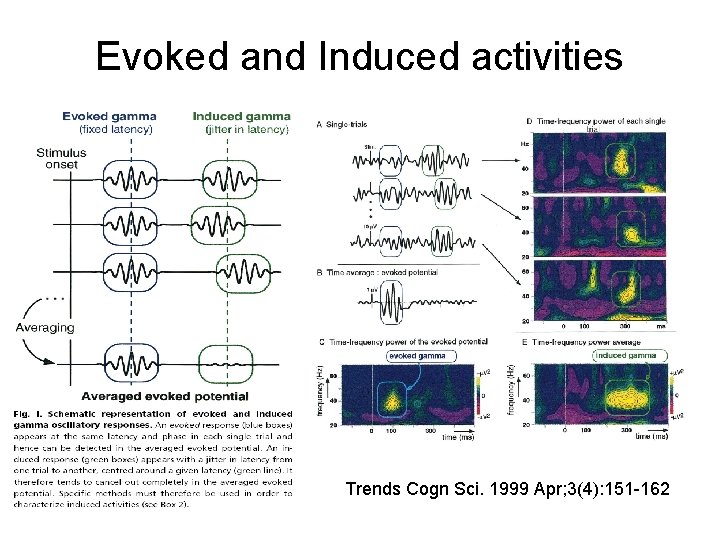
Evoked and Induced activities Trends Cogn Sci. 1999 Apr; 3(4): 151 -162

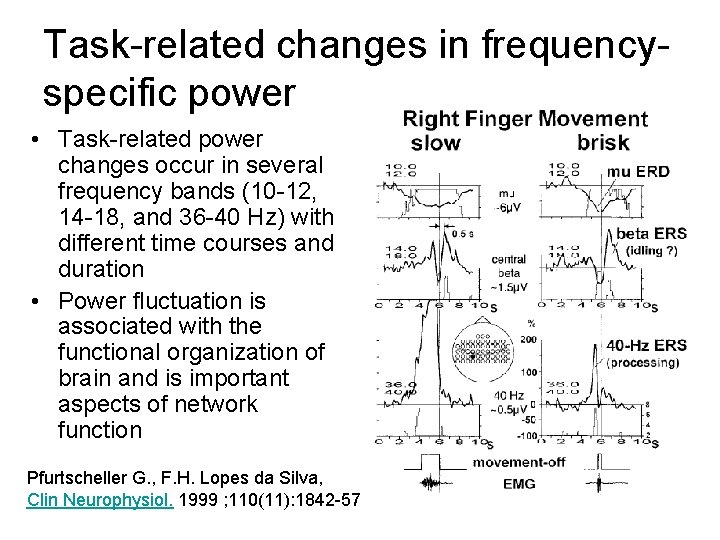
Task-related changes in frequencyspecific power • Task-related power changes occur in several frequency bands (10 -12, 14 -18, and 36 -40 Hz) with different time courses and duration • Power fluctuation is associated with the functional organization of brain and is important aspects of network function Pfurtscheller G. , F. H. Lopes da Silva, Clin Neurophysiol. 1999 ; 110(11): 1842 -57

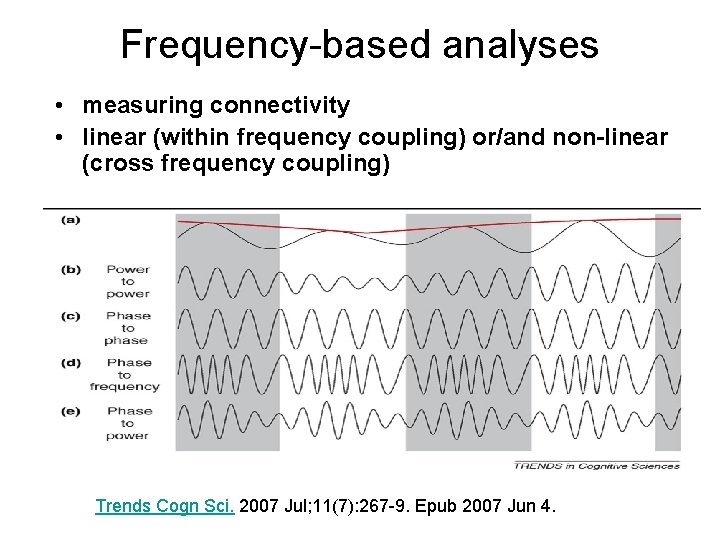
Frequency-based analyses • measuring connectivity • linear (within frequency coupling) or/and non-linear (cross frequency coupling) Trends Cogn Sci. 2007 Jul; 11(7): 267 -9. Epub 2007 Jun 4.

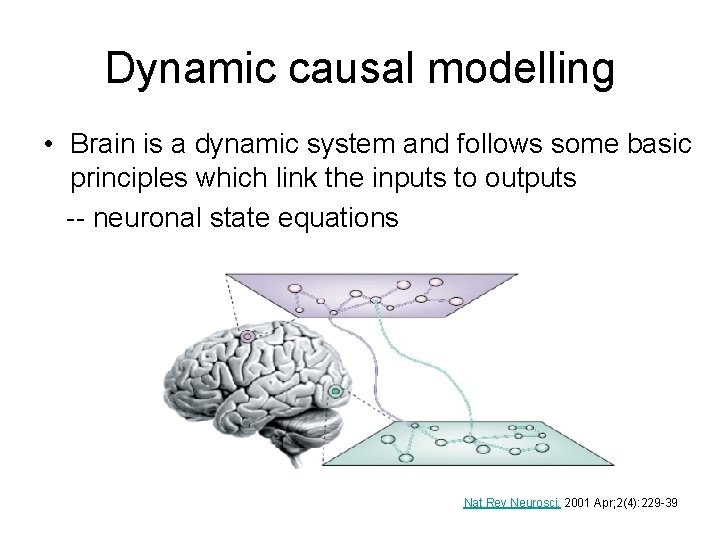
Dynamic causal modelling • Brain is a dynamic system and follows some basic principles which link the inputs to outputs -- neuronal state equations Nat Rev Neurosci. 2001 Apr; 2(4): 229 -39

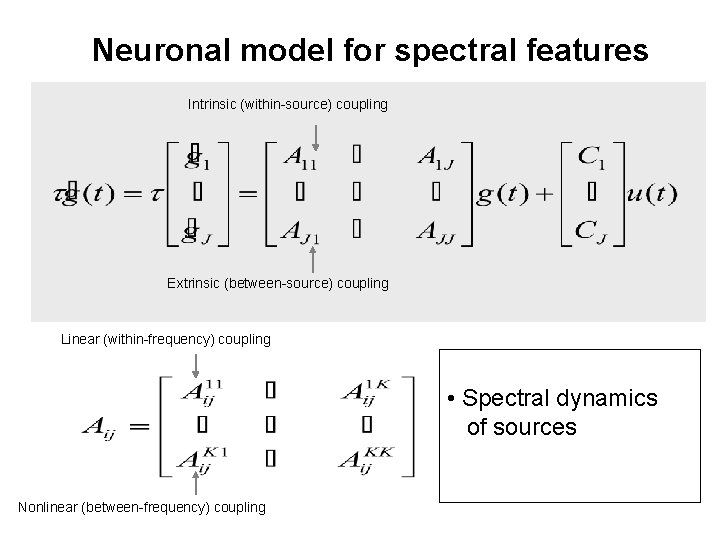
Neuronal model for spectral features Intrinsic (within-source) coupling Extrinsic (between-source) coupling Linear (within-frequency) coupling • Spectral dynamics of sources Nonlinear (between-frequency) coupling

Feature selection Inversion of electromagnetic model L input Data in channel space K frequency modes in j-th source • In theory, we can consider the states as spectral densities at a discrete number of frequencies. • In practice, we use only several significant singular components (modes) obtained by SVD of the spectral responses over time and sources so that we reduce the problem to modelling only the coupling among modes that cover all frequencies more than one state in different proportions per area

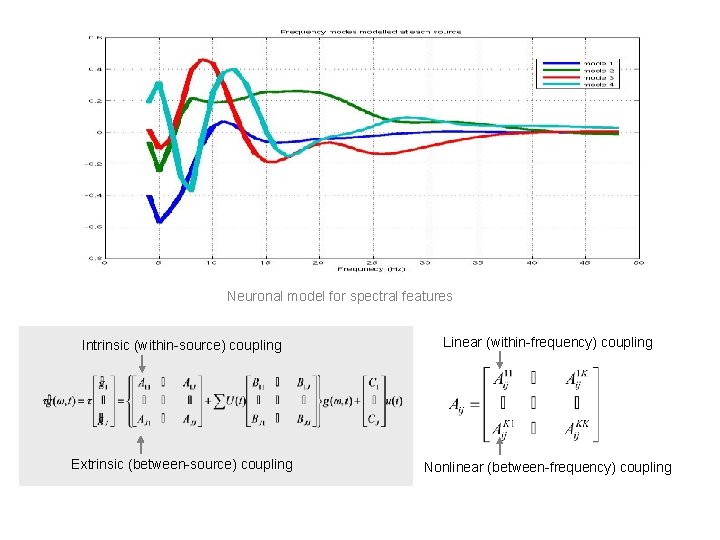
Neuronal model for spectral features Intrinsic (within-source) coupling Linear (within-frequency) coupling Extrinsic (between-source) coupling Nonlinear (between-frequency) coupling

Dynamic Causal Modelling • Specify a generative Specify the DCM: • areas • Exogenous inputs (stimuli) model based on • Extrinsic and intrinsic coupling specific hypotheses • The coupling parameters embody linear and non-linear connections. • Inversion of the models using a Bayesian procedure • With Bayesian model selection (BMC), one can use model evidence to compare several plausible models and identify the architecture that best explains the data.

Experimental examples -- A nonlinear neural code of motor programme during handgrip tasks (one condition) -- Forward and backward connections in the brain: A DCM study of functional asymmetries in face processing (faces v. s. scrambled faces )

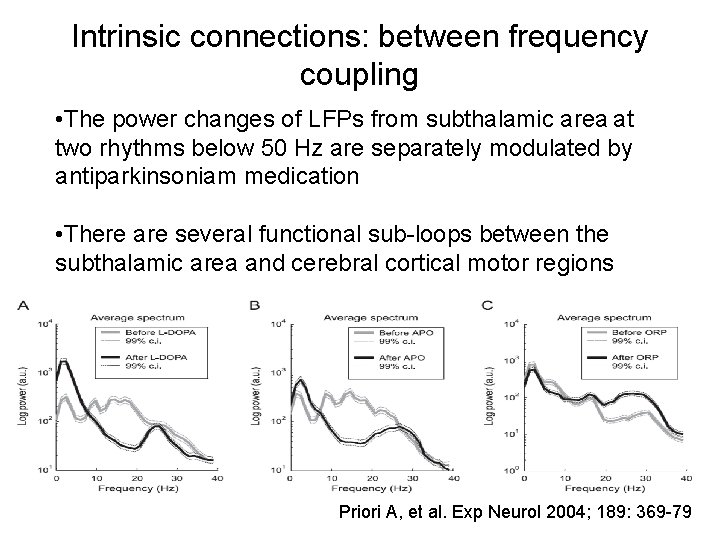
Intrinsic connections: between frequency coupling • The power changes of LFPs from subthalamic area at two rhythms below 50 Hz are separately modulated by antiparkinsoniam medication • There are several functional sub-loops between the subthalamic area and cerebral cortical motor regions Priori A, et al. Exp Neurol 2004; 189: 369 -79

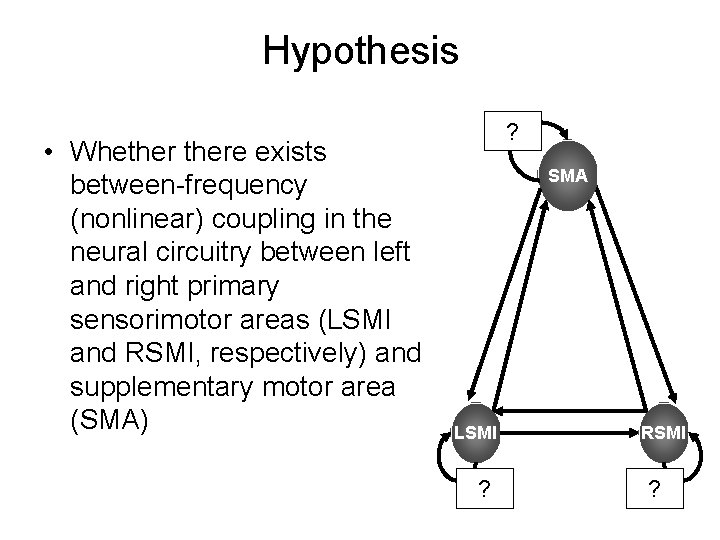
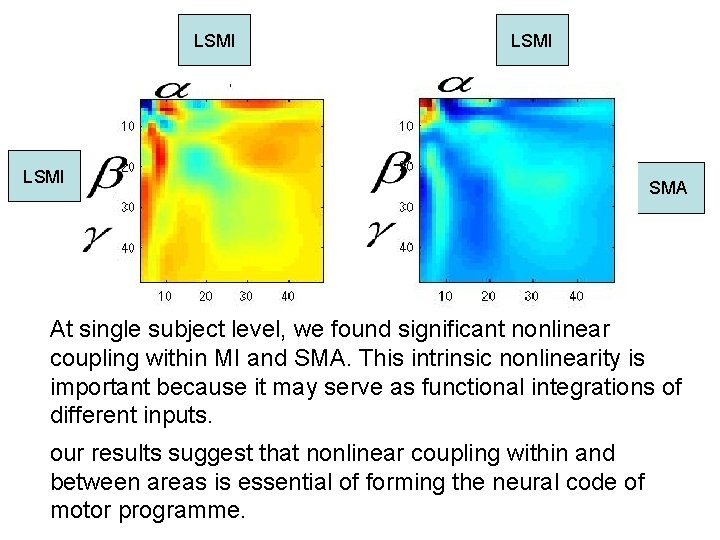
Hypothesis • Whethere exists between-frequency (nonlinear) coupling in the neural circuitry between left and right primary sensorimotor areas (LSMI and RSMI, respectively) and supplementary motor area (SMA) ? SMA LSMI ? RSMI ?

Motor task • Single isometric hand grip (Ward et al. 2003) • Inter-movement interval : 7 s + time jitter • The target forces: 15% and 45% of the right hand maximum voluntary contraction (MVC) • 100 trials of each event type

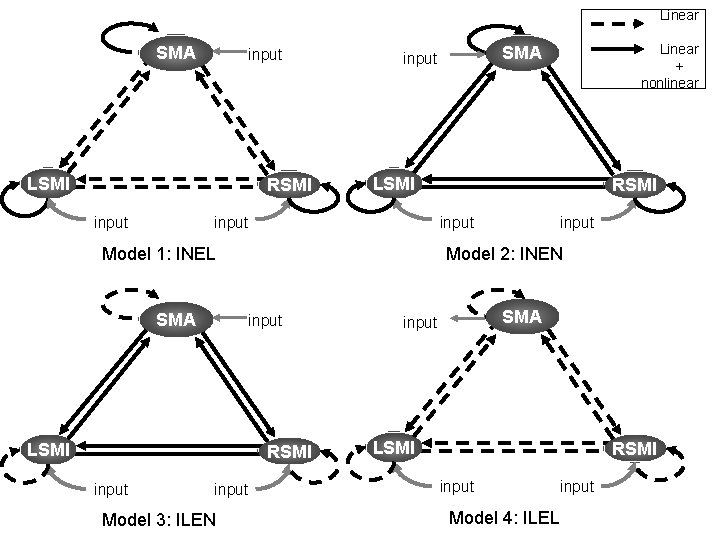
Four models • • Intrinsic Linear & Extrinsic Linear (ILEL) Intrinsic Linear & Extrinsic Nonlinear(ILEN) Intrinsic Nonlinear & Extrinsic Linear(LNEL) Intrinsic Nonlinear & Extrinsic Nonlinear (LNEN)

Linear SMA input LSMI RSMI input LSMI Model 1: INEL input RSMI input Model 3: ILEN input Model 2: INEN LSMI input RSMI input SMA Linear + nonlinear SMA input LSMI RSMI input Model 4: ILEL

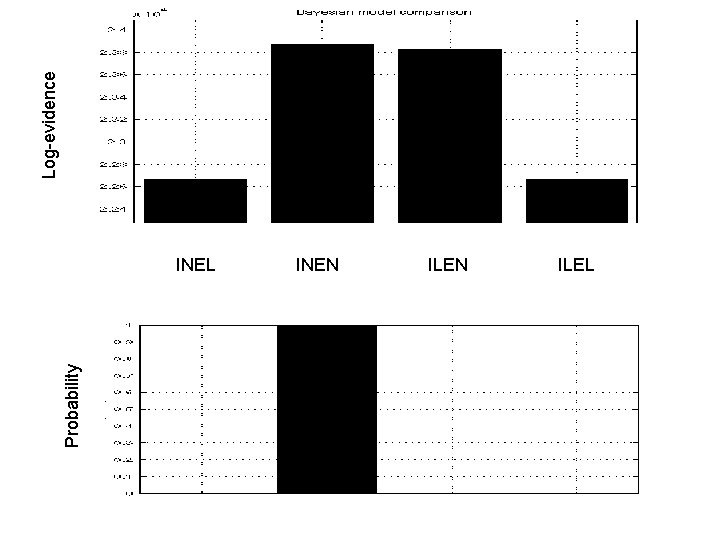
Log-evidence Probability INEL INEN ILEL

1 3 2

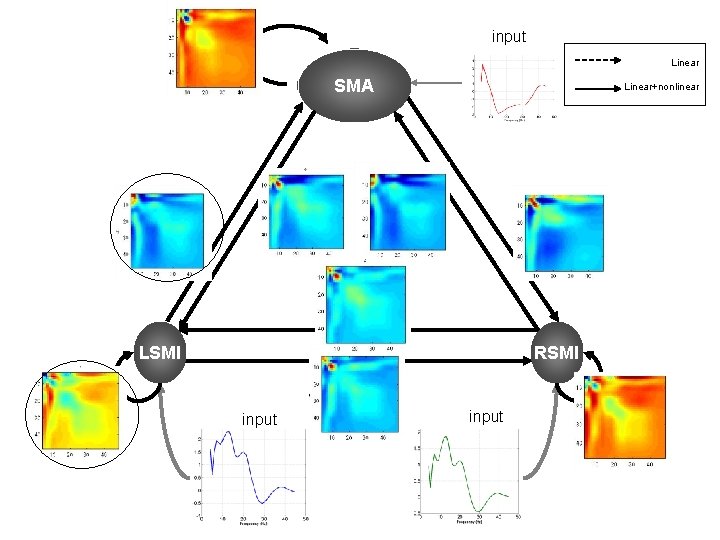
input Linear SMA Linear+nonlinear LSMI RSMI input

LSMI SMA At single subject level, we found significant nonlinear coupling within MI and SMA. This intrinsic nonlinearity is important because it may serve as functional integrations of different inputs. our results suggest that nonlinear coupling within and between areas is essential of forming the neural code of motor programme.

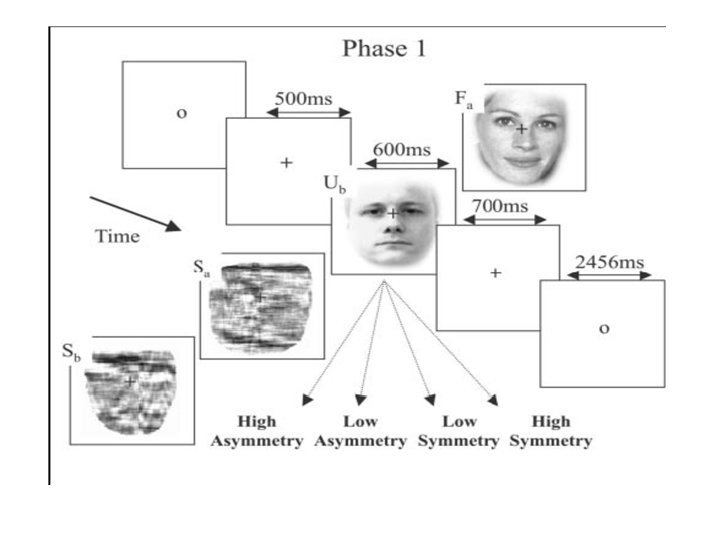
Forward and backward connections in the brain: A DCM study of functional asymmetries in face processing (faces v. s. scrambled faces )

Hierarchical connections and functional asysmetries • The brain has a hierarchical organisation that is largely defined by asysmetries in extrinsic cortico-cortical connections (anatomical and physiological evidence) • From animal and f. MRI studies, it has been shown that there is direct evidence for modulatory effect of backward connections is nonlinear

Hypothesis • If there any functional asymmetries in forward and backward connections during face processing • The models with nonlinearities in the backward modulation would be better than equivalent models with nonlinear forward modulation.

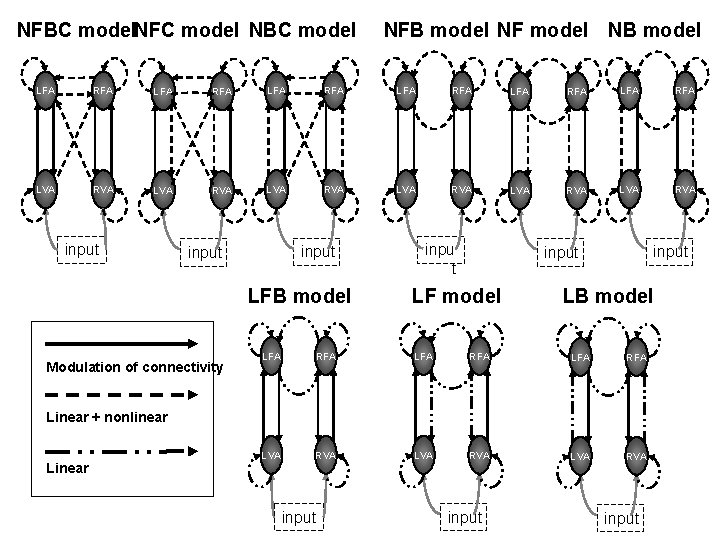
NFBC model. NFC model NBC model NFB model NF model NB model LFA RFA LFA RFA LVA RVA LVA RVA input LFB model Modulation of connectivity inpu t input LF model LB model LFA RFA LVA RVA Linear + nonlinear Linear input

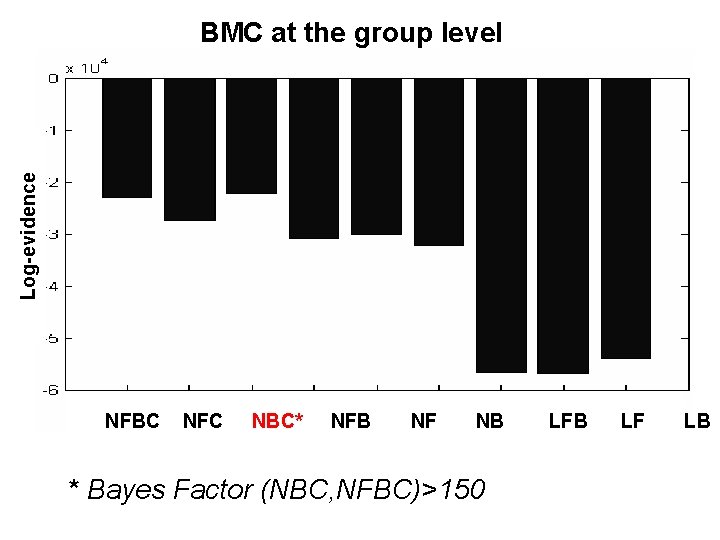
Log-evidence BMC at the group level NFBC NFC NBC* NFB NF NB * Bayes Factor (NBC, NFBC)>150 LFB LF LB

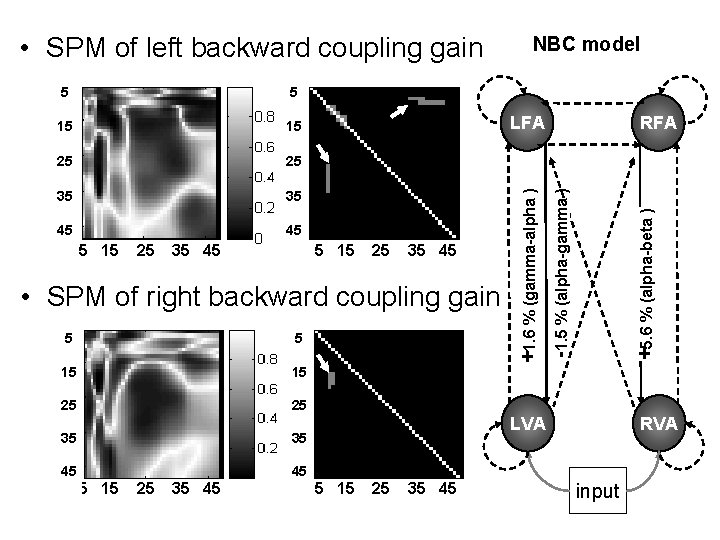
• SPM of left backward coupling gain 15 25 25 35 35 45 45 5 15 25 35 45 LFA 5 15 25 35 45 • SPM of right backward coupling gain 5 5 15 15 25 25 35 35 45 45 5 15 25 35 45 RFA +5. 6 % (alpha-beta ) 15 -1. 5 % (alpha-gamma ) 5 +1. 6 % (gamma-alpha ) 5 NBC model LVA 5 15 25 35 45 RVA input

conclusions • we were able to characterise frequencyspecific causal influences mediating the observed spectral responses. • we provide evidence for functional asymmetries in forward and backward connections.

Summary In DCM for induced responses : • modelling the second-order features of the data (i. e. , the spectrum) (broadband approach) • disambiguating between linear and non-linear coupling • making inferences about causal coupling • Making inference about task manipulation • DCM is not for a surrogate for widely used linear models (e. g. , coherence, correlations) but represents a complementary approach to disclose cross-frequency interactions

Thank you for your attention SPM 5 / SPM 8 Software available from http: //www. fil. ion. ucl. ac. uk/spm/

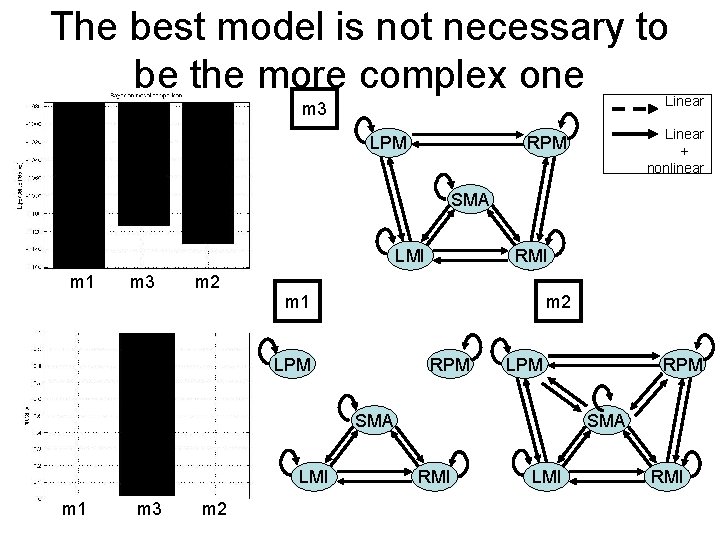
The best model is not necessary to be the more complex one Linear m 3 LPM Linear + nonlinear RPM SMA LMI m 1 m 3 m 2 RMI m 1 m 2 LPM RPM LPM SMA LMI m 1 m 3 m 2 RPM SMA RMI LMI RMI