Dynamic Causal Modelling DCM for f MRI Andre

Dynamic Causal Modelling (DCM) for f. MRI Andre Marreiros Wellcome Trust Centre for Neuroimaging University College London

Overview Dynamic Causal Modelling of f. MRI Definitions & motivation The neuronal model (bilinear dynamics) The Haemodynamic model Estimation: Bayesian framework DCM latest Extensions

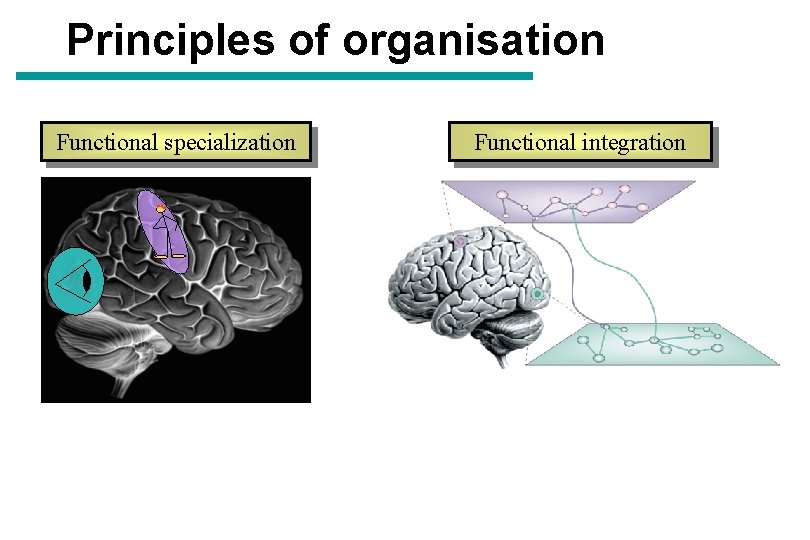
Principles of organisation Functional specialization Functional integration

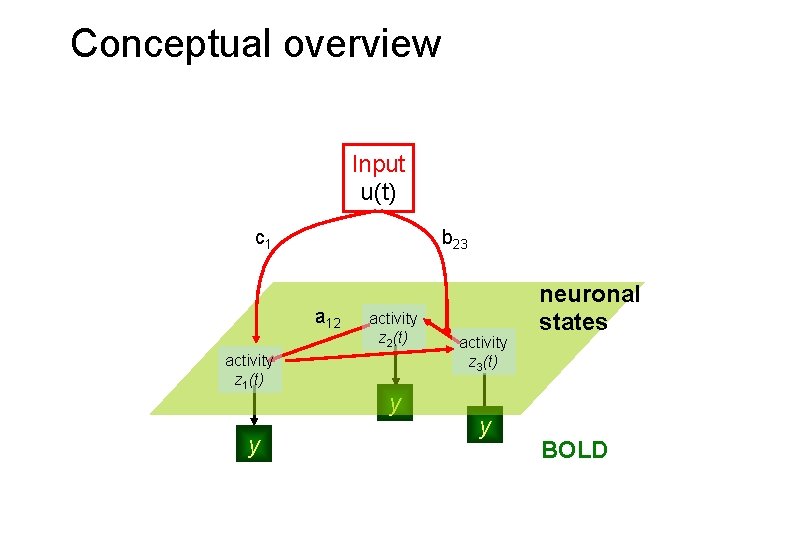
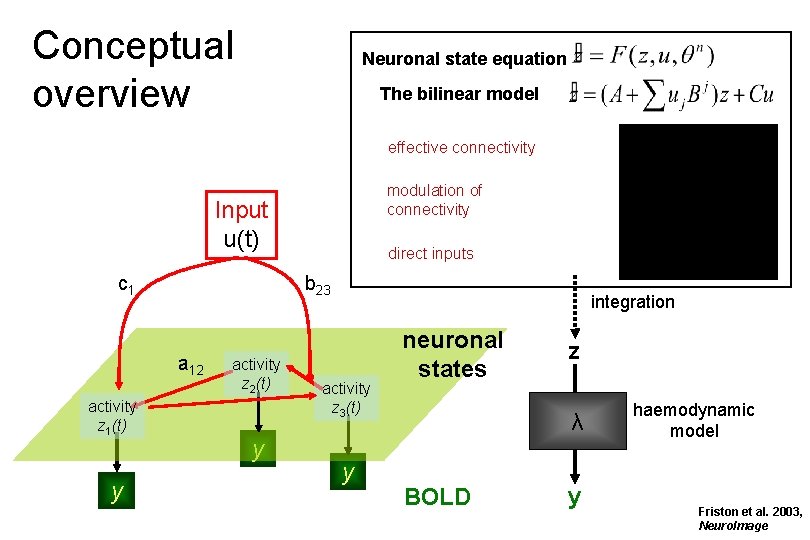
Conceptual overview Input u(t) c 1 b 23 a 12 activity z 1(t) y activity z 2(t) y activity z 3(t) y neuronal states BOLD

Use differential equations to represent a neuronal system • State vector – Changes with time • Rate of change of state vector – Interactions between elements – External inputs, u • System parameters system represented by state variables

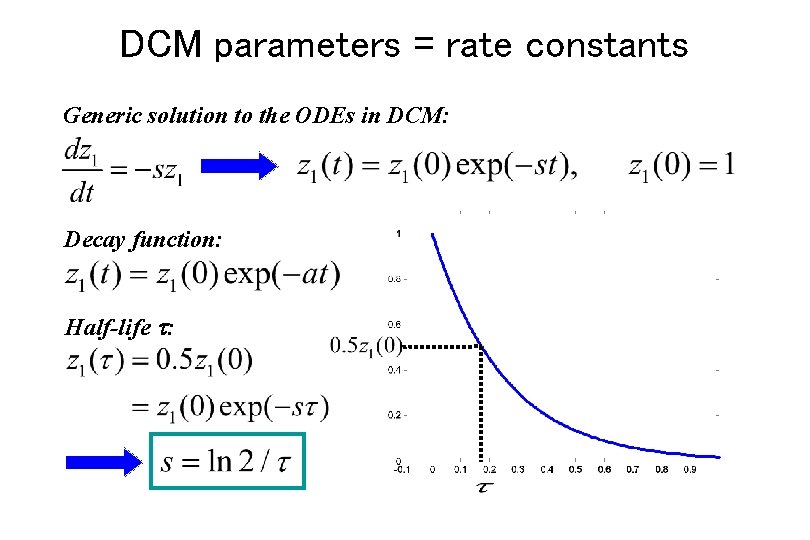
DCM parameters = rate constants Generic solution to the ODEs in DCM: Decay function: Half-life :

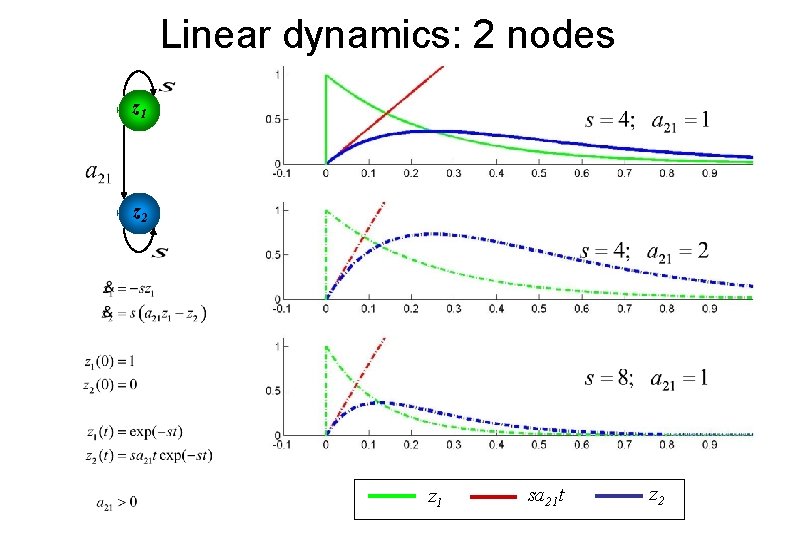
Linear dynamics: 2 nodes z 1 z 2 z 1 sa 21 t z 2

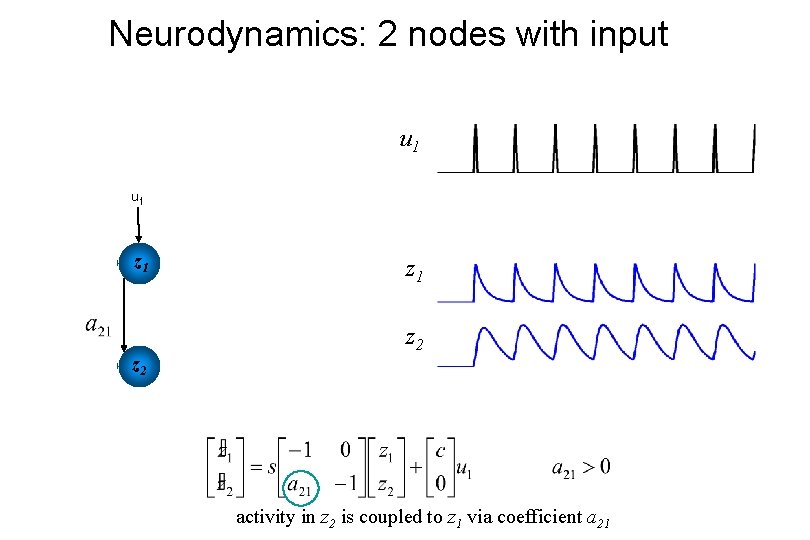
Neurodynamics: 2 nodes with input u 1 u 2 z 1 z 2 activity in z 2 is coupled to z 1 via coefficient a 21

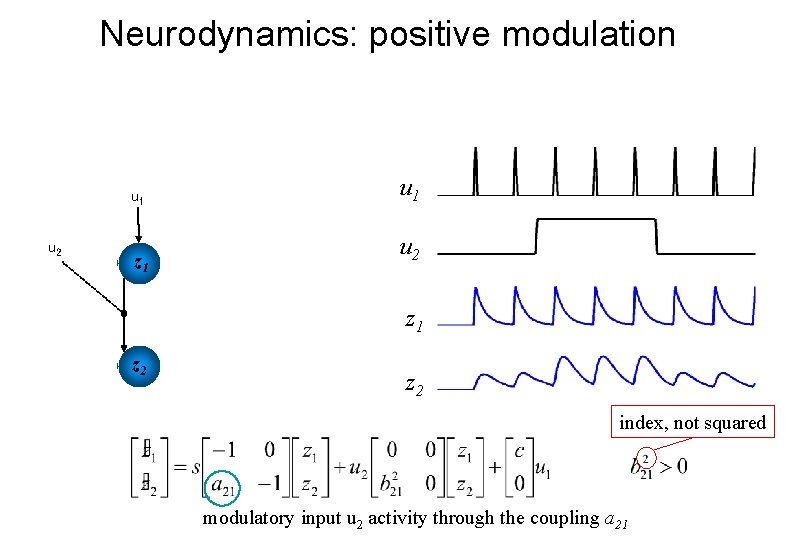
Neurodynamics: positive modulation u 1 u 2 z 1 z 2 index, not squared modulatory input u 2 activity through the coupling a 21

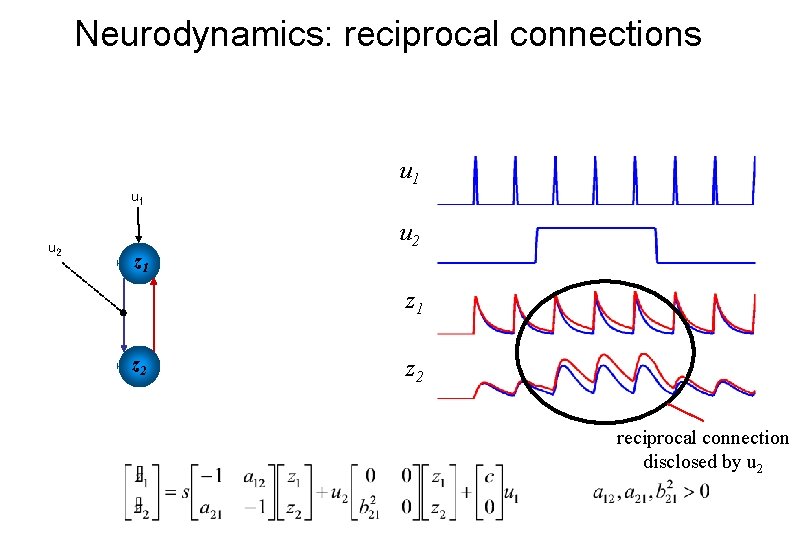
Neurodynamics: reciprocal connections u 1 u 2 z 1 z 2 reciprocal connection disclosed by u 2

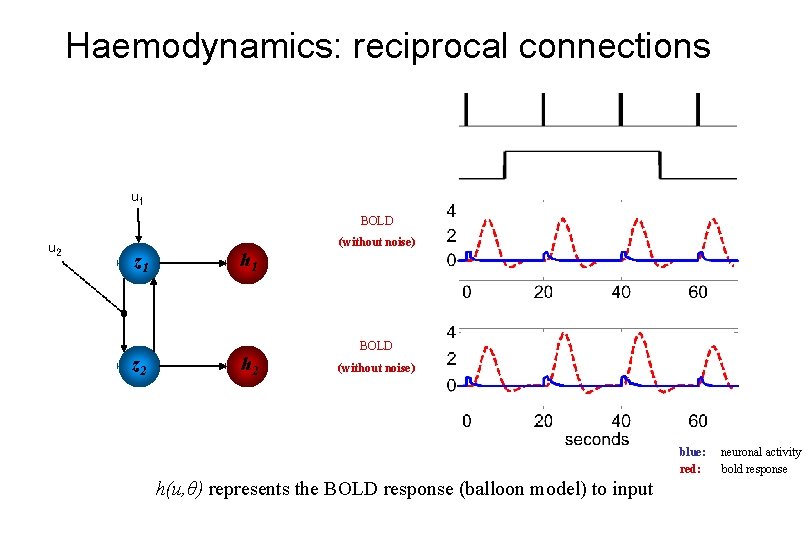
Haemodynamics: reciprocal connections u 1 BOLD u 2 z 1 z 2 h 1 h 2 (without noise) BOLD (without noise) blue: red: h(u, θ) represents the BOLD response (balloon model) to input neuronal activity bold response

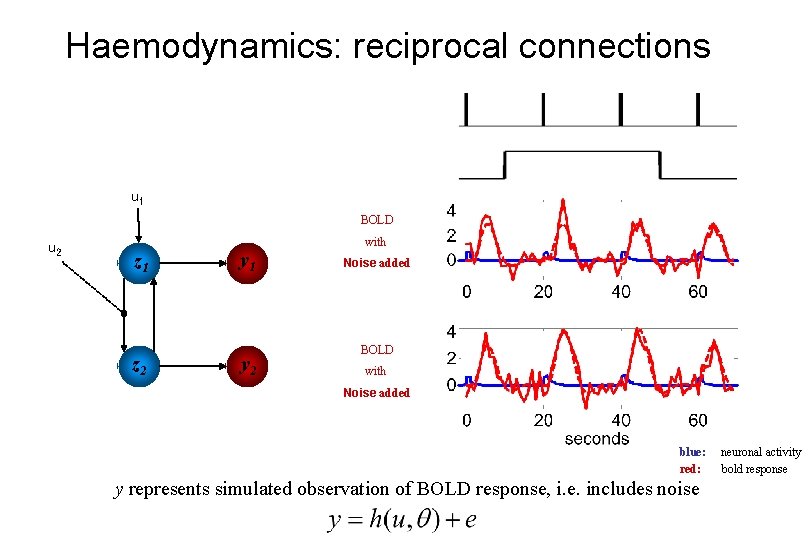
Haemodynamics: reciprocal connections u 1 BOLD u 2 z 1 z 2 y 1 y 2 with Noise added BOLD with Noise added blue: red: y represents simulated observation of BOLD response, i. e. includes noise neuronal activity bold response

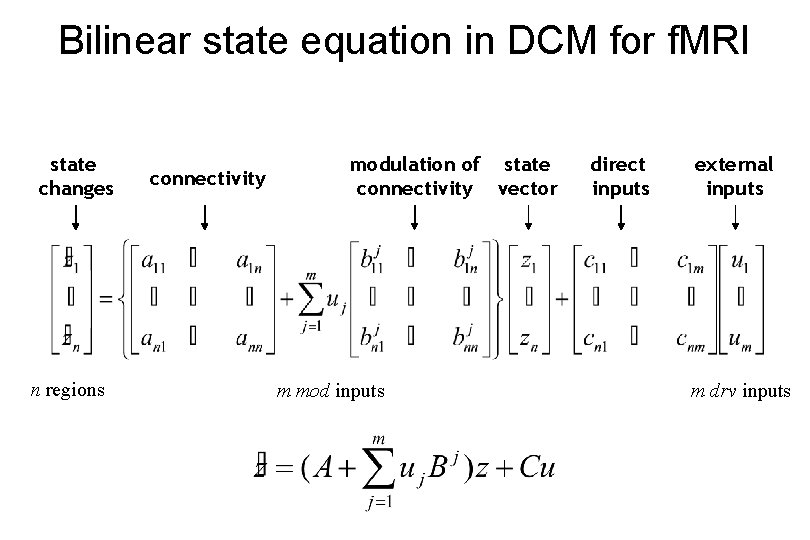
Bilinear state equation in DCM for f. MRI state changes n regions connectivity modulation of state connectivity vector m mod inputs direct inputs external inputs m drv inputs

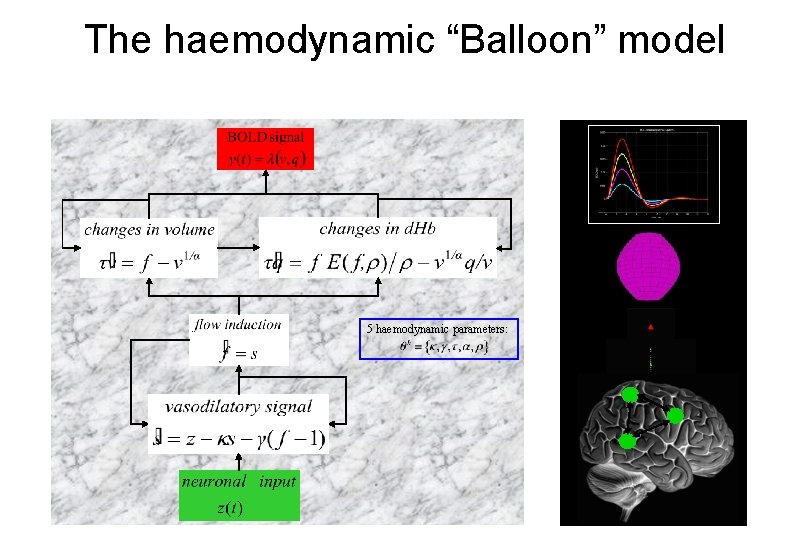
The haemodynamic “Balloon” model 5 haemodynamic parameters:

Conceptual overview Neuronal state equation The bilinear model effective connectivity modulation of connectivity Input u(t) c 1 b 23 a 12 activity z 1(t) y direct inputs activity z 2(t) y integration activity z 3(t) y neuronal states z λ BOLD y haemodynamic model Friston et al. 2003, Neuro. Image

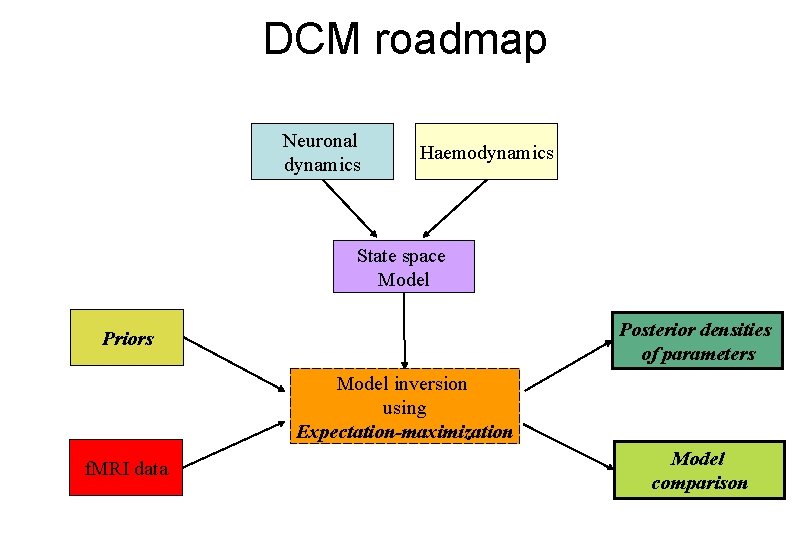
DCM roadmap Neuronal dynamics Haemodynamics State space Model Posterior densities of parameters Priors Model inversion using Expectation-maximization f. MRI data Model comparison

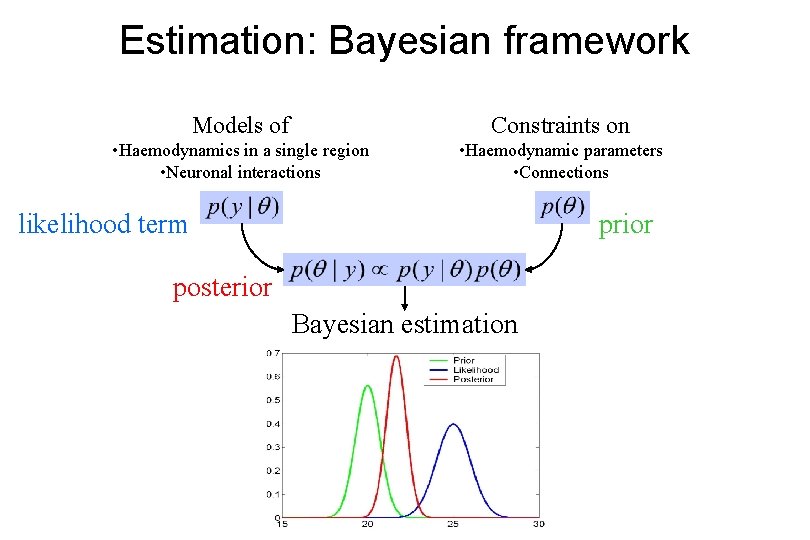
Estimation: Bayesian framework Models of Constraints on • Haemodynamics in a single region • Neuronal interactions • Haemodynamic parameters • Connections likelihood term prior posterior Bayesian estimation

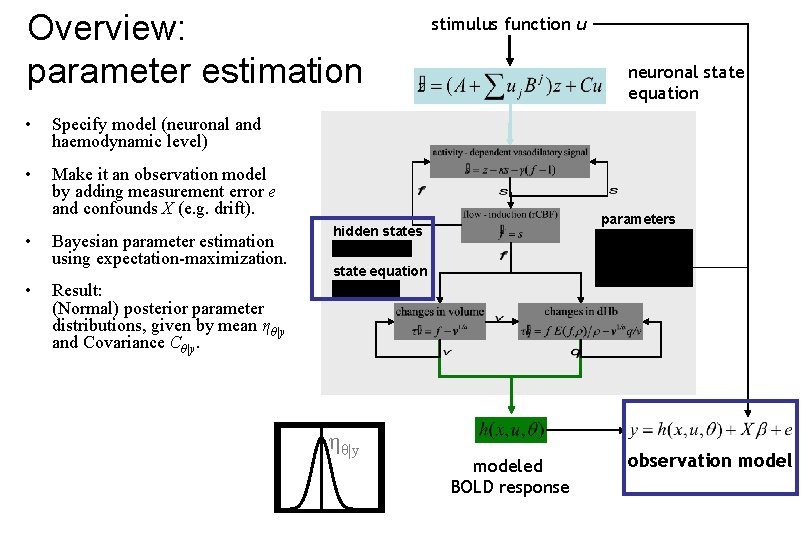
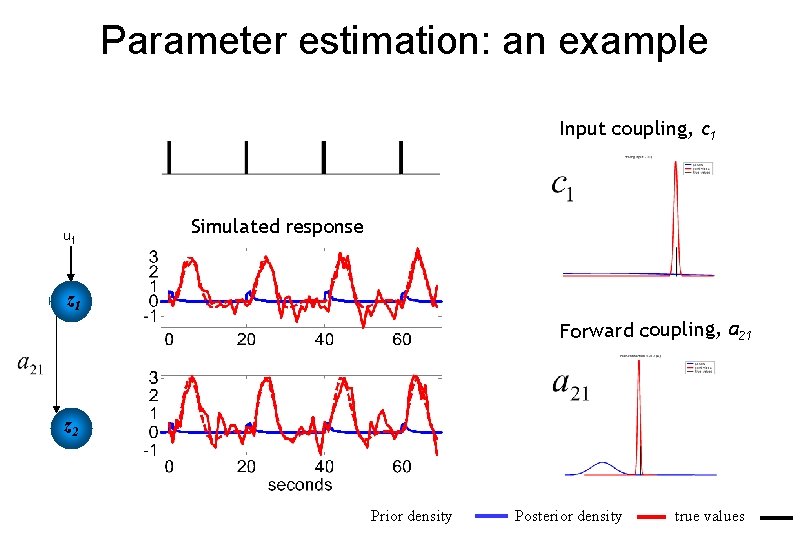
Overview: parameter estimation • Specify model (neuronal and haemodynamic level) • Make it an observation model by adding measurement error e and confounds X (e. g. drift). • • Bayesian parameter estimation using expectation-maximization. stimulus function u neuronal state equation parameters hidden states state equation Result: (Normal) posterior parameter distributions, given by mean ηθ|y and Covariance Cθ|y. ηθ|y modeled BOLD response observation model

Parameter estimation: an example Input coupling, c 1 u 1 Simulated response z 1 Forward coupling, a 21 z 2 Prior density Posterior density true values

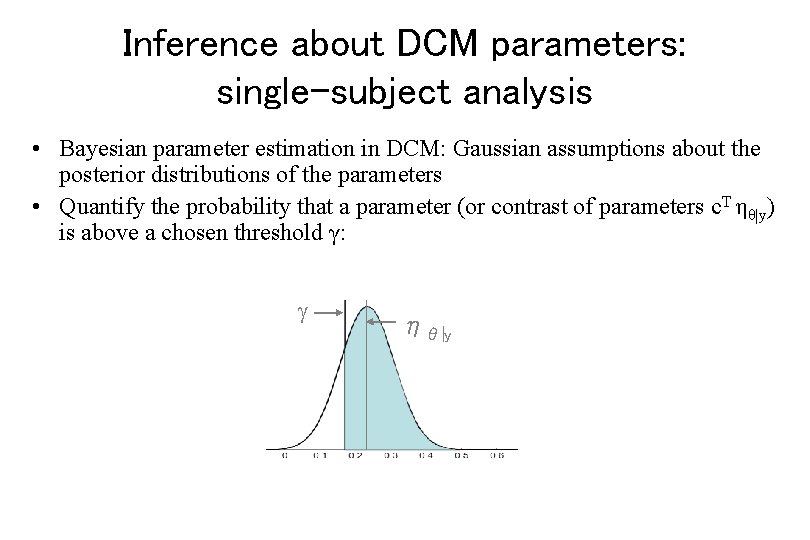
Inference about DCM parameters: single-subject analysis • Bayesian parameter estimation in DCM: Gaussian assumptions about the posterior distributions of the parameters • Quantify the probability that a parameter (or contrast of parameters c. T ηθ|y) is above a chosen threshold γ: ηθ|y

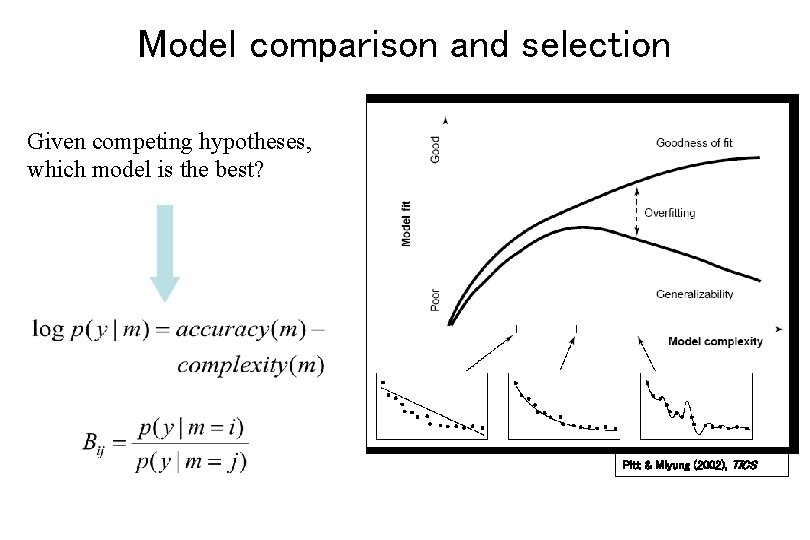
Model comparison and selection Given competing hypotheses, which model is the best? Pitt & Miyung (2002), TICS

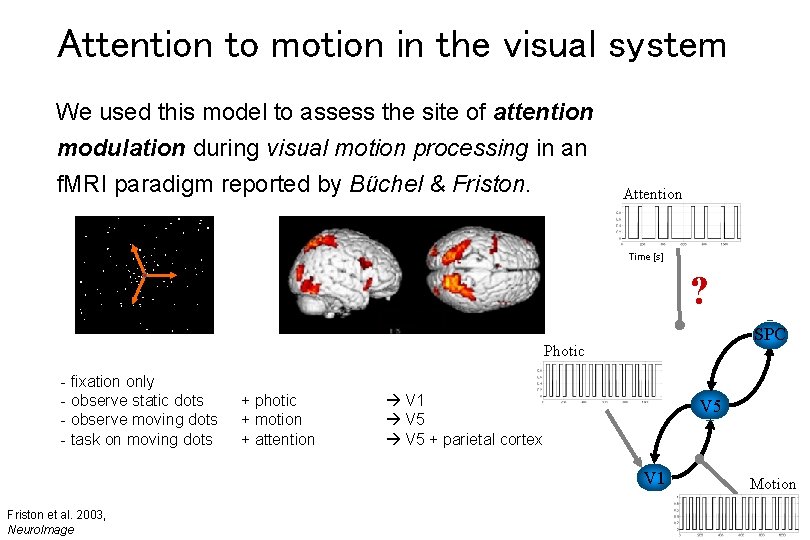
Attention to motion in the visual system We used this model to assess the site of attention modulation during visual motion processing in an f. MRI paradigm reported by Büchel & Friston. Attention Time [s] ? SPC Photic - fixation only - observe static dots - observe moving dots - task on moving dots + photic + motion + attention V 1 V 5 + parietal cortex V 5 V 1 Friston et al. 2003, Neuro. Image Motion

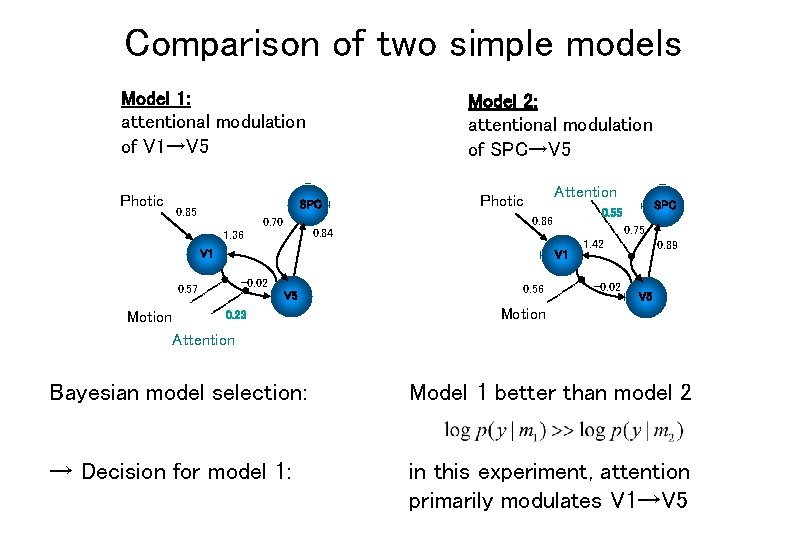
Comparison of two simple models Model 1: attentional modulation of V 1→V 5 Photic Model 2: attentional modulation of SPC→V 5 SPC 0. 85 Attention Photic 0. 86 0. 70 V 1 -0. 02 0. 57 Motion 0. 75 0. 84 1. 36 V 5 0. 23 0. 56 SPC 0. 55 1. 42 -0. 02 0. 89 V 5 Motion Attention Bayesian model selection: Model 1 better than model 2 → Decision for model 1: in this experiment, attention primarily modulates V 1→V 5

• potential timing problem in DCM: temporal shift between regional time series because of multi-slice acqisition slice acquisition Extension I: Slice timing model 2 1 visual input • Solution: – Modelling of (known) slice timing of each area. Slice timing extension now allows for any slice timing differences! Long TRs (> 2 sec) no longer a limitation. (Kiebel et al. , 2007)

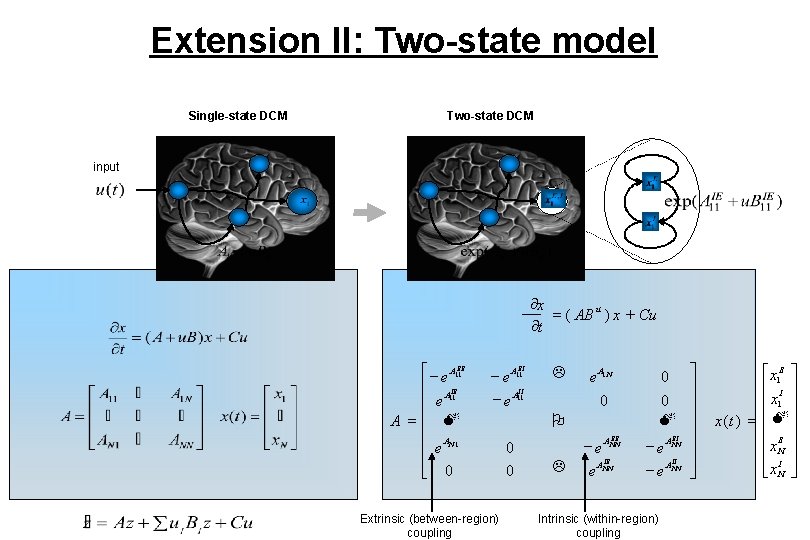
Extension II: Two-state model Single-state DCM Two-state DCM input ¶x = ( AB u ) x + Cu ¶t é - e A 11 EE ê A IE ê e 11 A =ê M ê A ê e N 1 ê ë 0 EI - e A 11 II - e A 11 Extrinsic (between-region) coupling L e A 1 N 0 0 M 0 O 0 0 EE - e ANN L e IE ANN EI - e ANN Intrinsic (within-region) coupling ù ú ú ú û é x 1 E ù ê I ú ê x 1 ú x (t ) = ê M ú ê E ú êx. N ú êx I ú ë N û

Example: Two-state Model Comparison - BCW DCM for Büchel & Friston Attention b - Intr Attention - FWD Attention

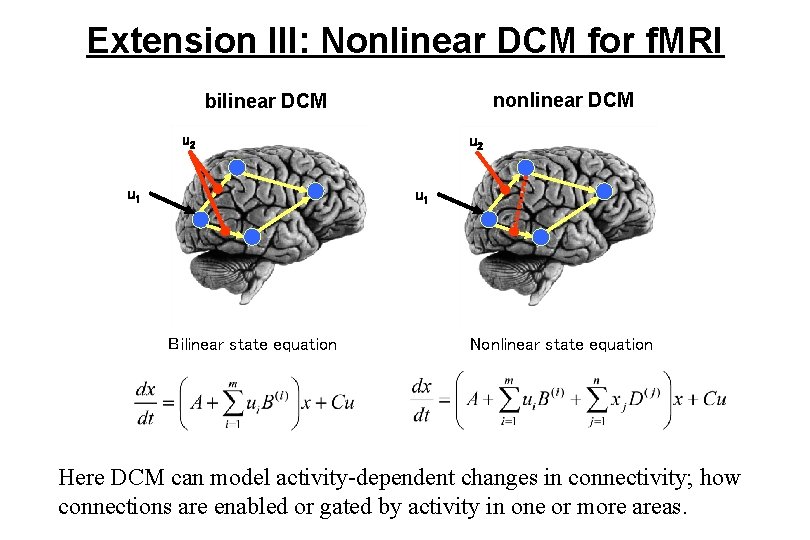
Extension III: Nonlinear DCM for f. MRI nonlinear DCM bilinear DCM u 2 u 1 Bilinear state equation Nonlinear state equation Here DCM can model activity-dependent changes in connectivity; how connections are enabled or gated by activity in one or more areas.

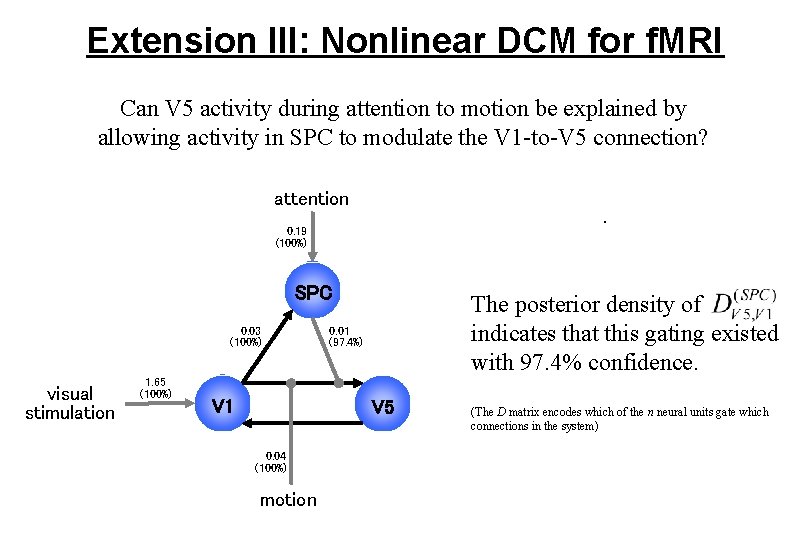
Extension III: Nonlinear DCM for f. MRI Can V 5 activity during attention to motion be explained by allowing activity in SPC to modulate the V 1 -to-V 5 connection? attention . 0. 19 (100%) SPC 0. 03 (100%) visual stimulation 1. 65 (100%) V 1 The posterior density of indicates that this gating existed with 97. 4% confidence. 0. 01 (97. 4%) V 5 0. 04 (100%) motion (The D matrix encodes which of the n neural units gate which connections in the system)

Conclusions Dynamic Causal Modelling (DCM) of f. MRI is mechanistic model that is informed by anatomical and physiological principles. DCM uses a deterministic differential equation to model neuro-dynamics (represented by matrices A, B and C) DCM uses a Bayesian framework to estimate model parameters DCM provides an observation model for neuroimaging data, e. g. f. MRI, M/EEG DCM is not model or modality specific (Models will change and the method extended to other modalities e. g. ERPs)